万字长文概览深度学习的可解释性研究

极市导读
本文深入浅出的介绍了深度学习可解释性的概念、方法以及深度学习可解释性相关工作的研究成果。>>加入极市CV技术交流群,走在计算机视觉的最前沿
深度学习的可解释性研究(一):让模型具备说人话的能力
1. 可解释性是什么?
广义上的可解释性指在我们需要了解或解决一件事情的时候,我们可以获得我们所需要的足够的可以理解的信息。比如我们在调试bug的时候,需要通过变量审查和日志信息定位到问题出在哪里。比如在科学研究中面临一个新问题的研究时,我们需要查阅一些资料来了解这个新问题的基本概念和研究现状,以获得对研究方向的正确认识。反过来理解,如果在一些情境中我们无法得到相应的足够的信息,那么这些事情对我们来说都是不可解释的。比如刘慈欣的短篇《朝闻道》中霍金提出的“宇宙的目的是什么”这个问题一下子把无所不知的排险者卡住了,因为再高等的文明都没办法理解和掌握造物主创造宇宙时的全部信息,这些终极问题对我们来说永远都是不可解释的。
而具体到机器学习领域来说,以最用户友好的决策树模型为例,模型每作出一个决策都会通过一个决策序列来向我们展示模型的决策依据:比如男性&未婚&博士&秃头的条件对应“不感兴趣”这个决策,而且决策树模型自带的基于信息理论的筛选变量标准也有助于帮助我们理解在模型决策产生的过程中哪些变量起到了显著的作用。所以在一定程度上,我们认为决策树模型是一个具有比较好的可解释性的模型,在以后的介绍中我们也会讲到,以决策树为代表的规则模型在可解释性研究方面起到了非常关键的作用。再以用户最不友好的多层神经网络模型为例,模型产生决策的依据是什么呢?大概是以比如 1/(e^-(2*1/(e^(-(2*x+y))+1) + 3*1/(e^(-(8*x+5*y))+1))+1) 是否大于0.5为标准(这已经是最简单的模型结构了),这一连串的非线性函数的叠加公式让人难以直接理解神经网络的“脑回路”,所以深度神经网络习惯性被大家认为是黑箱模型。
17年ICML的Tutorial中给出的一个关于可解释性的定义是:
Interpretation is the process of giving explanations to Human.
总结一下就是“说人话”,“说人话”,“说人话”,不以人类可以理解的方式给出的解释都叫耍流氓,记住这三个字,你就差不多把握了可解释性的精髓所在。
2. 我们为什么需要可解释性?
广义上来说我们对可解释性的需求主要来源于对问题和任务了解得还不够充分。具体到深度学习/机器学习领域,就像我们上文提到的多层神经网络存在的问题,尽管高度的非线性赋予了多层神经网络极高的模型表示能力,配合一些堪称现代炼丹术的调参技术可以在很多问题上达到非常喜人的表现,大家如果经常关注AI的头条新闻,那些机器学习和神经网络不可思议的最新突破甚至经常会让人产生AI马上要取代人类的恐惧和幻觉。但正如近日贝叶斯网络的创始人Pearl所指出的,“几乎所有的深度学习突破性的本质上来说都只是些曲线拟合罢了”,他认为今天人工智能领域的技术水平只不过是上一代机器已有功能的增强版。虽然我们造出了准确度极高的机器,但最后只能得到一堆看上去毫无意义的模型参数和拟合度非常高的判定结果,但实际上模型本身也意味着知识,我们希望知道模型究竟从数据中学到了哪些知识(以人类可以理解的方式表达的)从而产生了最终的决策。从中是不是可以帮助我们发现一些潜在的关联,比如我想基于深度学习模型开发一个帮助医生判定病人风险的应用,除了最终的判定结果之外,我可能还需要了解模型产生这样的判定是基于病人哪些因素的考虑。如果一个模型完全不可解释,那么在很多领域的应用就会因为没办法给出更多可靠的信息而受到限制。这也是为什么在深度学习准确率这么高的情况下,仍然有一大部分人倾向于应用可解释性高的传统统计学模型的原因。
不可解释同样也意味着危险,事实上很多领域对深度学习模型应用的顾虑除了模型本身无法给出足够的信息之外,也有或多或少关于安全性的考虑。比如,下面一个非常经典的关于对抗样本的例子,对于一个CNN模型,在熊猫的图片中添加了一些噪声之后却以99.3%的概率被判定为长臂猿。

在熊猫图片中加入噪声,模型以99.3%的概率将图片识别为长臂猿
事实上其他一些可解释性较好的模型面对的对抗样本问题可能甚至比深度学习模型更多,但具备可解释性的模型在面对这些问题的时候是可以对异常产生的原因进行追踪和定位的,比如线性回归模型中我们可以发现某个输入参数过大/过小导致了最后判别失常。但深度学习模型很难说上面这两幅图到底是因为哪些区别导致了判定结果出现了如此大的偏差。尽管关于对抗样本的研究最近也非常火热,但依然缺乏具备可解释性的关于这类问题的解释。
当然很多学者对可解释性的必要性也存有疑惑,在NIPS 2017会场上,曾进行了一场非常激烈火爆的主题为“可解释性在机器学习中是否必要”的辩论,大家对可解释性的呼声还是非常高的。但人工智能三巨头之一的Yann LeCun却认为:人类大脑是非常有限的,我们没有那么多脑容量去研究所有东西的可解释性。有些东西是需要解释的,比如法律,但大多数情况下,它们并没有你想象中那么重要。比如世界上有那么多应用、网站,你每天用Facebook、Google的时候,你也没想着要寻求它们背后的可解释性。LeCun也举了一个例子:他多年前和一群经济学家也做了一个模型来预测房价。第一个用的简单的线性于猜测模型,经济学家也能解释清楚其中的原理;第二个用的是复杂的神经网络,但效果比第一个好上不少。结果,这群经济学家想要开公司做了。你说他们会选哪个?LeCun表示,任何时候在这两种里面选择都会选效果好的。就像很多年里虽然我们不知道药物里的成分但一直在用一样。
但是不可否认的是,可解释性始终是一个非常好的性质,如果我们能兼顾效率、准确度、说人话这三个方面,具备可解释性模型将在很多应用场景中具有不可替代的优势。
3. 有哪些可解释性方法?
我们之前也提到机器学习的目的是从数据中发现知识或解决问题,那么在这个过程中只要是能够提供给我们关于数据或模型的可以理解的信息,有助于我们更充分地发现知识、理解和解决问题的方法,那么都可以归类为可解释性方法。如果按照可解释性方法进行的过程进行划分的话,大概可以划分为三个大类:
1. 在建模之前的可解释性方法
2. 建立本身具备可解释性的模型
3. 在建模之后使用可解释性方法对模型作出解释
4. 在建模之前的可解释性方法
这一类方法其实主要涉及一些数据预处理或数据展示的方法。机器学习解决的是从数据中发现知识和规律的问题,如果我们对想要处理的数据特征所知甚少,指望对所要解决的问题本身有很好的理解是不现实的,在建模之前的可解释性方法的关键在于帮助我们迅速而全面地了解数据分布的特征,从而帮助我们考虑在建模过程中可能面临的问题并选择一种最合理的模型来逼近问题所能达到的最优解。
数据可视化方法就是一类非常重要的建模前可解释性方法。很多对数据挖掘稍微有些了解的人可能会认为数据可视化是数据挖掘工作的最后一步,大概就是通过设计一些好看又唬人的图表或来展示你的分析挖掘成果。但大多数时候,我们在真正要研究一个数据问题之前,通过建立一系列方方面面的可视化方法来建立我们对数据的直观理解是非常必须的,特别是当数据量非常大或者数据维度非常高的时候,比如一些时空高维数据,如果可以建立一些一些交互式的可视化方法将会极大地帮助我们从各个层次角度理解数据的分布,在这个方面我们实验室也做过一些非常不错的工作。
还有一类比较重要的方法是探索性质的数据分析,可以帮助我们更好地理解数据的分布情况。比如一种称为MMD-critic方法中,可以帮助我们找到数据中一些具有代表性或者不具代表性的样本。

使用MMD-critic从Imagenet数据集中学到的代表性样本和非代表性样本(以两种狗为例)
5. 建立本身具备可解释性的模型
建立本身具备可解释性的模型是我个人觉得是最关键的一类可解释性方法,同样也是一类要求和限定很高的方法,具备“说人话”能力的可解释性模型大概可以分为以下几种:
1. 基于规则的方法(Rule-based)
2. 基于单个特征的方法(Per-feature-based)
3. 基于实例的方法(Case-based)
4. 稀疏性方法(Sparsity)
5. 单调性方法(Monotonicity)
基于规则的方法比如我们提到的非常经典的决策树模型。这类模型中任何的一个决策都可以对应到一个逻辑规则表示。但当规则表示过多或者原始的特征本身就不是特别好解释的时候,基于规则的方法有时候也不太适用。
基于单个特征的方法主要是一些非常经典的线性模型,比如线性回归、逻辑回归、广义线性回归、广义加性模型等,这类模型可以说是现在可解释性最高的方法,可能学习机器学习或计算机相关专业的朋友会认为线性回归是最基本最低级的模型,但如果大家学过计量经济学,就会发现大半本书都在讨论线性模型,包括经济学及相关领域的论文其实大多数也都是使用线性回归作为方法来进行研究。这种非常经典的模型全世界每秒都会被用到大概800多万次。为什么大家这么青睐这个模型呢?除了模型的结构比较简单之外,更重要的是线性回归模型及其一些变种拥有非常solid的统计学基础,统计学可以说是最看重可解释性的一门学科了,上百年来无数数学家统计学家探讨了在各种不同情况下的模型的参数估计、参数修正、假设检验、边界条件等等问题,目的就是为了使得在各种不同情况下都能使模型具有有非常好的可解释性,如果大家有时间有兴趣的话,除了学习机器学习深度模型模型之外还可以尽量多了解一些统计学的知识,可能对一些问题会获得完全不一样的思考和理解。
基于实例的方法主要是通过一些代表性的样本来解释聚类/分类结果的方法。比如下图所展示的贝叶斯实例模型(Bayesian Case Model,BCM),我们将样本分成三个组团,可以分别找出每个组团中具有的代表性样例和重要的子空间。比如对于下面第一类聚类来说,绿脸是具有代表性的样本,而绿色、方块是具有代表性的特征子空间。
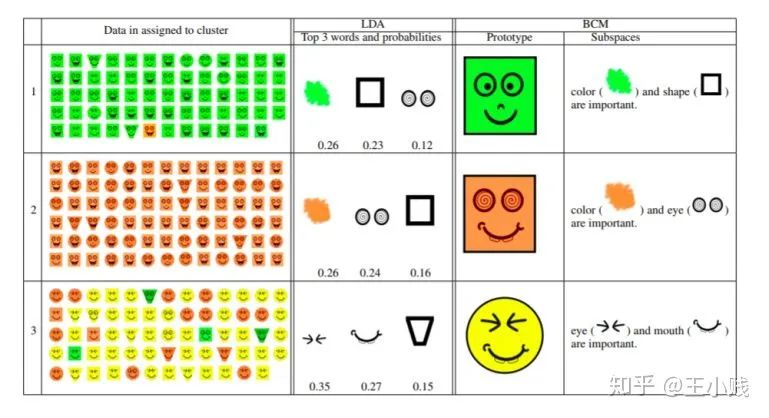
使用BCM学到的分类及其对应的代表性样本和代表性特征子空间
基于实例的方法的一些局限在于可能挑出来的样本不具有代表性或者人们可能会有过度泛化的倾向。
基于稀疏性的方法主要是利用信息的稀疏性特质,将模型尽可能地简化表示。比如如下图的一种图稀疏性的LDA方法,根据层次性的单词信息形成了层次性的主题表达,这样一些小的主题就可以被更泛化的主题所概括,从而可以使我们更容易理解特定主题所代表的含义。
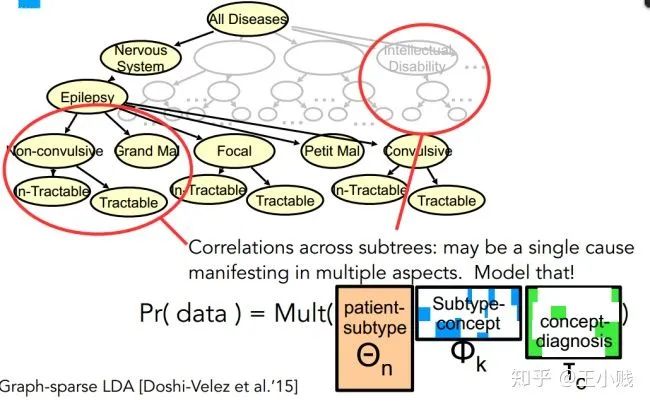
Graph-based LDA 中的主题层次结构
基于单调性的方法:在很多机器学习问题中,有一些输入和输出之间存在正相关/负相关关系,如果在模型训练中我们可以找出这种单调性的关系就可以让模型具有更高的可解释性。比如医生对患特定疾病的概率的估计主要由一些跟该疾病相关联的高风险因素决定,找出单调性关系就可以帮助我们识别这些高风险因素。
6. 在建模之后使用可解释性性方法作出解释
建模后的可解释性方法主要是针对具有黑箱性质的深度学习模型而言的,主要分为以下几类的工作:
1. 隐层分析方法
2. 模拟/代理模型
3. 敏感性分析方法
这部分是我们接下来介绍和研究的重点,因此主要放在后续的文章中进行讲解,在本篇中不作过多介绍。
除了对深度学习模型本身进行解释的方法之外,也有一部分工作旨在建立本身具有可解释性的深度学习模型,这和我们前面介绍通用的可解释性模型有区别也有联系,也放到后面的文章中进行介绍。
深度学习的可解释性研究(二):不如打开箱子看一看
1. 黑箱真的是黑箱吗?——深度学习的物质组成视角
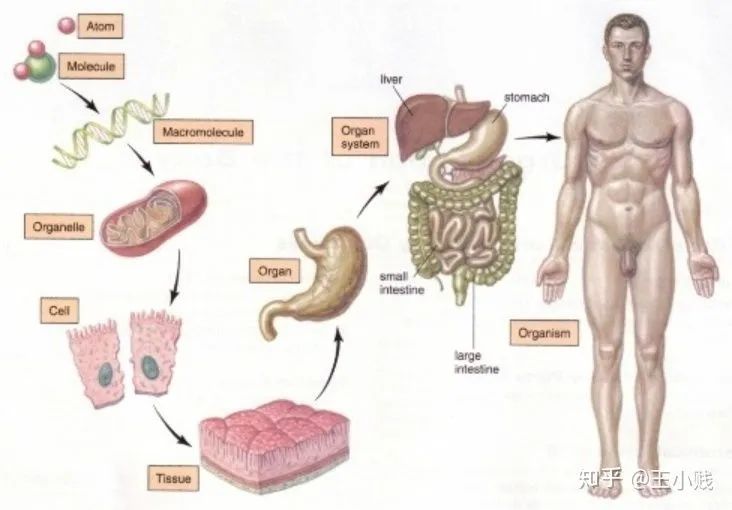
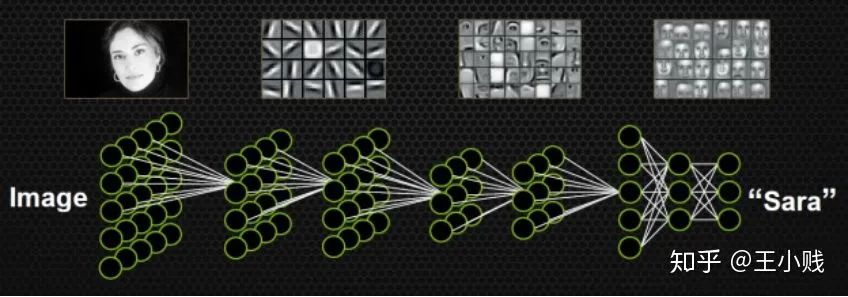
2. 模型学到了哪些概念?
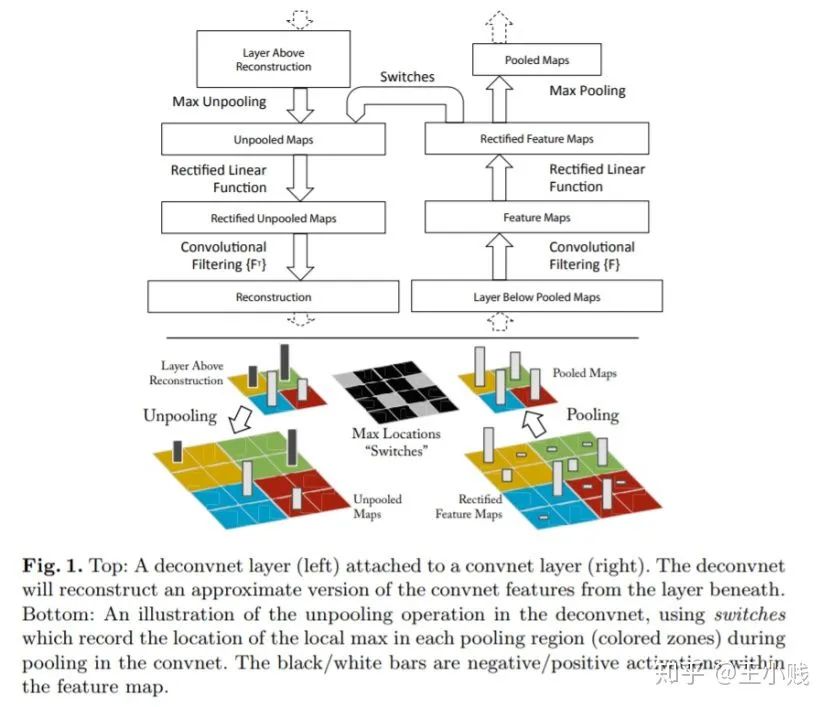
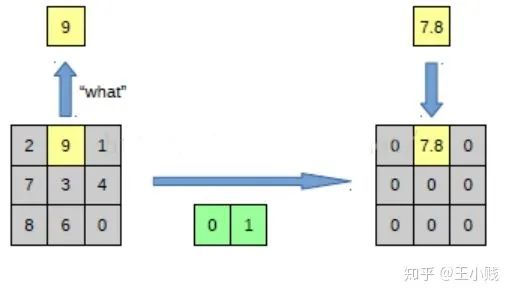
3. 反池化:
4. 反卷积:
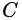 ,那么后一层和前一层的关系就可以表示为:
,那么后一层和前一层的关系就可以表示为:
 往往可以表示为卷积层对输入层的梯度,也就是说通过对卷积层进行适当的补0操作,再用原始的卷积核转置之后的卷积核进行卷积操作,就可以得到相应的梯度矩阵与当前卷积层的乘积,而我们在这里使用反池化-反激活之后的特征(其中包含了大部分为0的数值)进行该操作其实表征了原始输入对池化之后的特征的影响,因为在反激活过程中保证了所有值非负因此反卷积的过程中符号不会发生改变。
往往可以表示为卷积层对输入层的梯度,也就是说通过对卷积层进行适当的补0操作,再用原始的卷积核转置之后的卷积核进行卷积操作,就可以得到相应的梯度矩阵与当前卷积层的乘积,而我们在这里使用反池化-反激活之后的特征(其中包含了大部分为0的数值)进行该操作其实表征了原始输入对池化之后的特征的影响,因为在反激活过程中保证了所有值非负因此反卷积的过程中符号不会发生改变。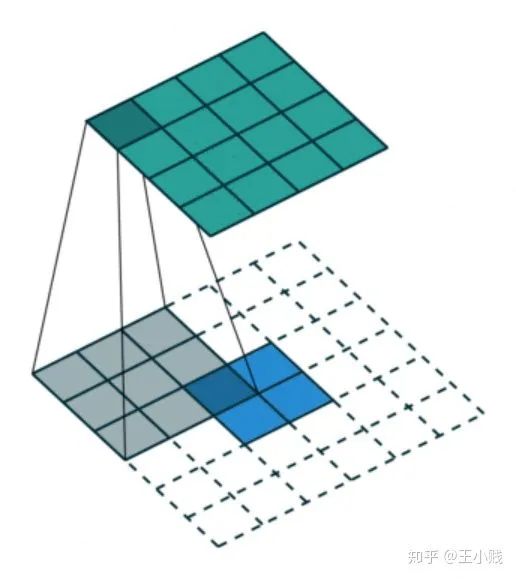

 (其实也就是feature map),这样就可以得到隐层k激活值的分布,对于每个隐层k,我们都可以找到一个
(其实也就是feature map),这样就可以得到隐层k激活值的分布,对于每个隐层k,我们都可以找到一个  使得
使得  ,这个
,这个  可以作为接下来判断区域是否激活的一个标准。
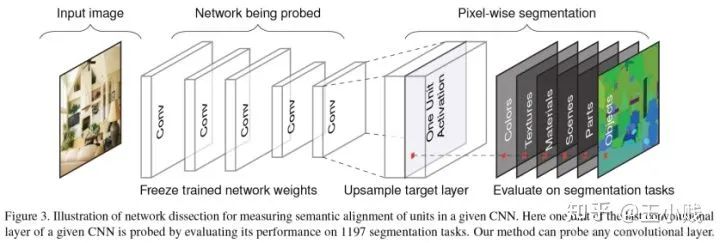
可以作为接下来判断区域是否激活的一个标准。 (其实就是标注出了相关概念在图像中的代表区域),我们将低分辨率的卷积层的特征图
(其实就是标注出了相关概念在图像中的代表区域),我们将低分辨率的卷积层的特征图  通过插值的方法扩展为和原始图片尺寸一样大的图像
通过插值的方法扩展为和原始图片尺寸一样大的图像  。
。 ,这样就得到了所有被激活的区域,而我们通过将
,这样就得到了所有被激活的区域,而我们通过将  和输入层的概念激活热图
和输入层的概念激活热图  作对比,这样就可以获得隐层-概念对的匹配程度:
作对比,这样就可以获得隐层-概念对的匹配程度: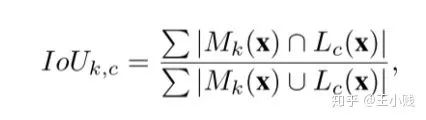
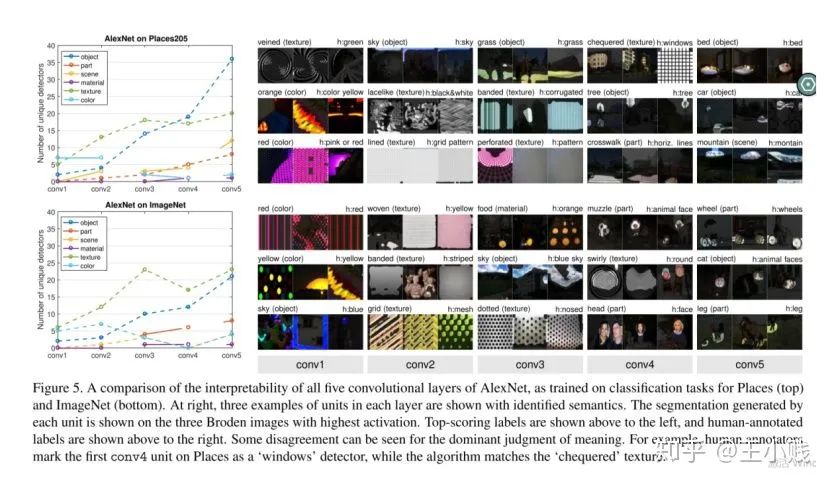
5. 低级到高级=泛化到特化?
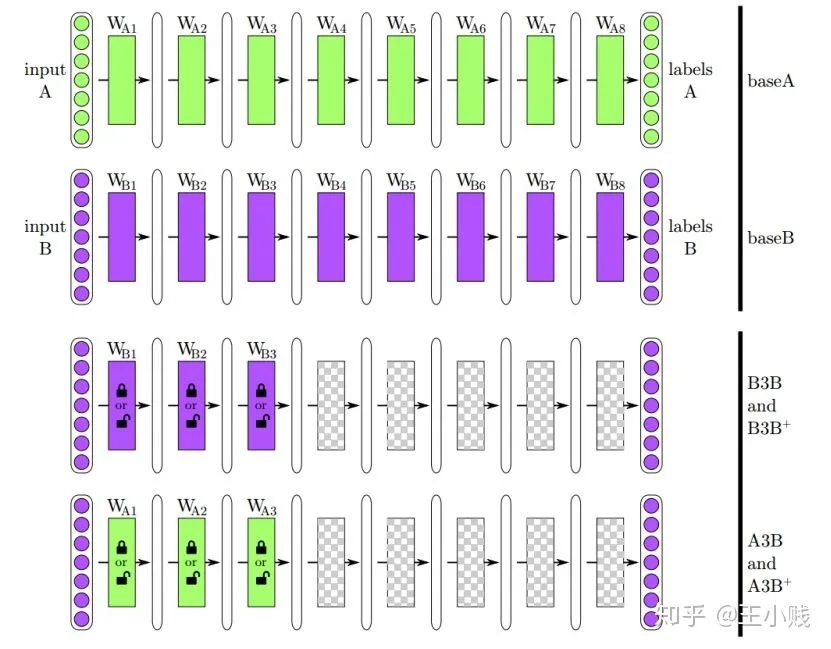
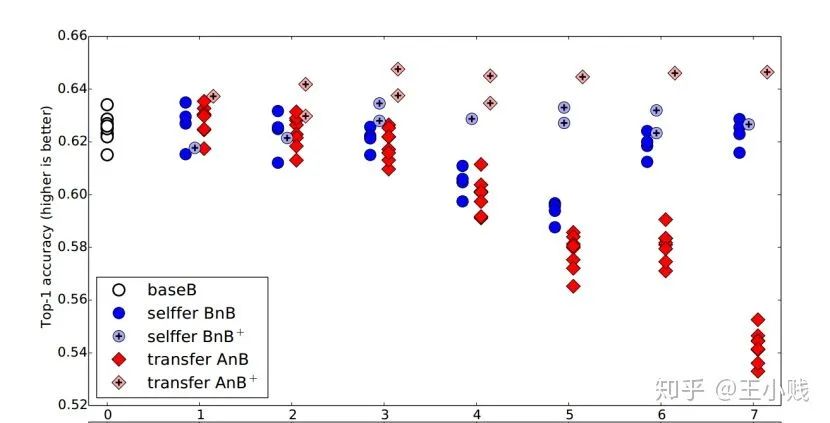
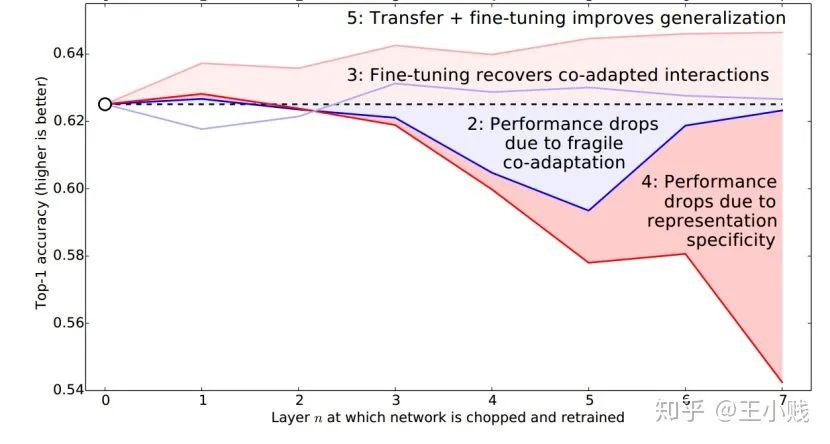
6. 真的需要那么多层吗?
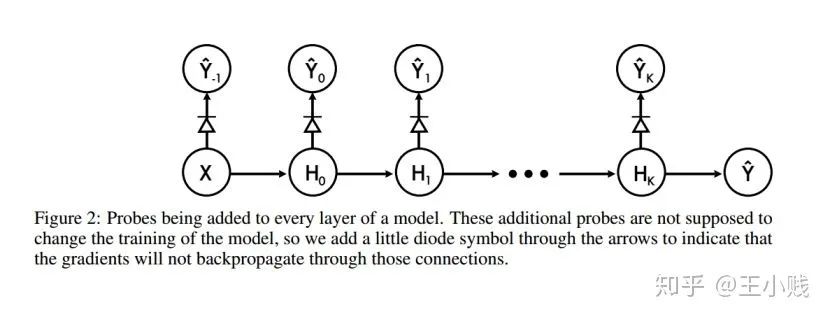
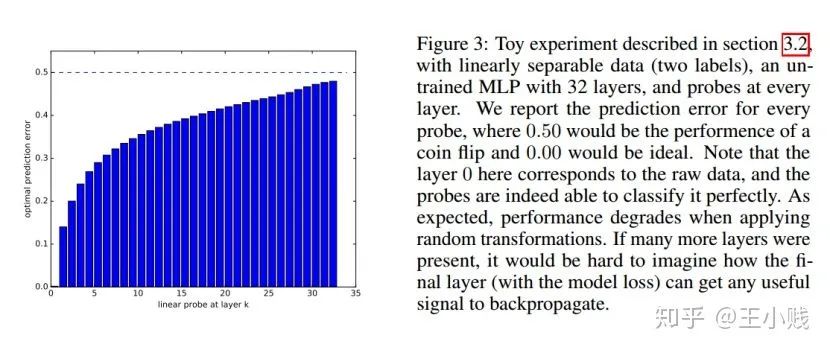
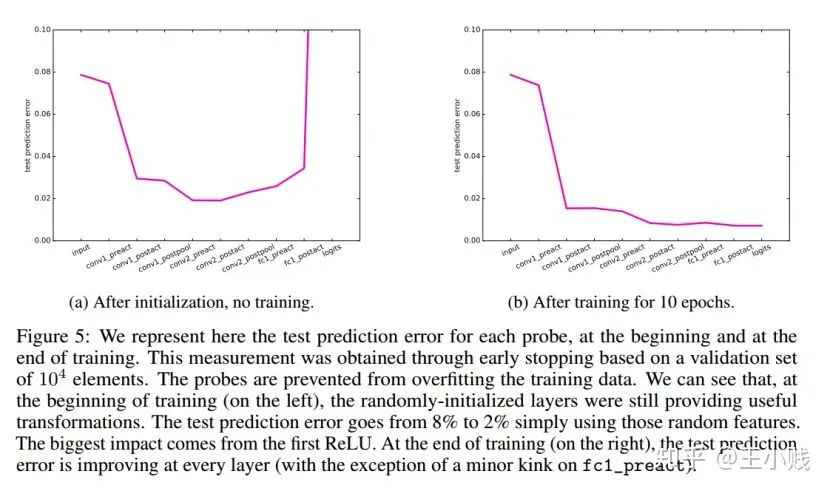
小结
深度学习的可解释性研究(三)——是谁在撩动琴弦
 ,敏感性分析就是令每个属性在可能的范围变动,研究和预测这些属性的变化对模型输出值的影响程度。我们将影响程度的大小称为该属性的敏感性系数,敏感性系数越大,就说明属性对模型输出的影响越大。一般来讲对于神经网络的敏感性分析方法可以分为变量敏感性分析、样本敏感性分析两种,变量敏感性分析用来检验输入属性变量对模型的影响程度,样本敏感性分析用来研究具体样本对模型的重要程度,也是敏感性分析研究的一个新方向。
,敏感性分析就是令每个属性在可能的范围变动,研究和预测这些属性的变化对模型输出值的影响程度。我们将影响程度的大小称为该属性的敏感性系数,敏感性系数越大,就说明属性对模型输出的影响越大。一般来讲对于神经网络的敏感性分析方法可以分为变量敏感性分析、样本敏感性分析两种,变量敏感性分析用来检验输入属性变量对模型的影响程度,样本敏感性分析用来研究具体样本对模型的重要程度,也是敏感性分析研究的一个新方向。1. 变量敏感性分析
 对输出变量
对输出变量  的影响程度为:
的影响程度为:
 的正负性导致我们可能没办法得到真实的敏感性系数,所以后来就对这个公式进行了改造,改为用绝对值来评估影响力。
的正负性导致我们可能没办法得到真实的敏感性系数,所以后来就对这个公式进行了改造,改为用绝对值来评估影响力。
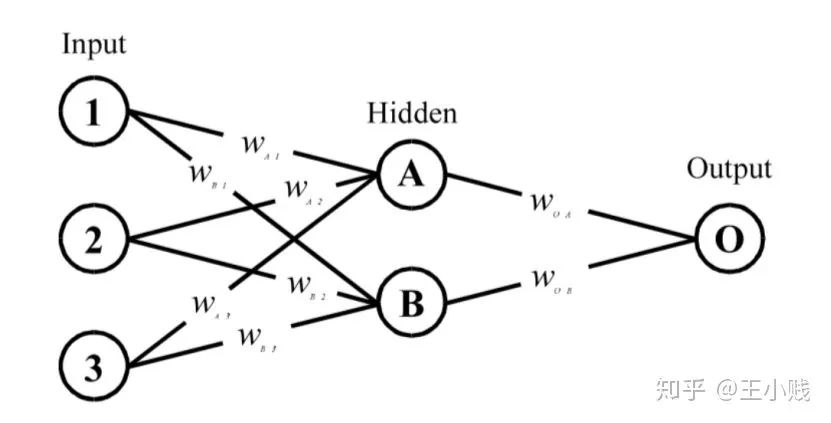




 )
) 和初始的随机权重构建一个神经网络
和初始的随机权重构建一个神经网络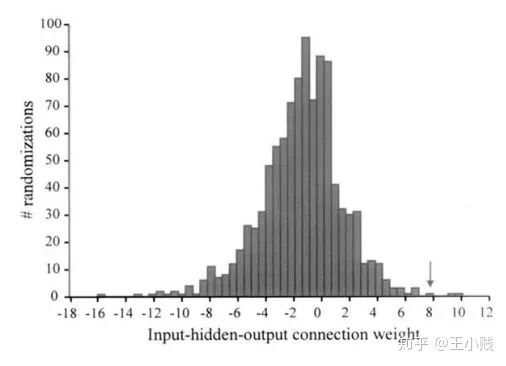
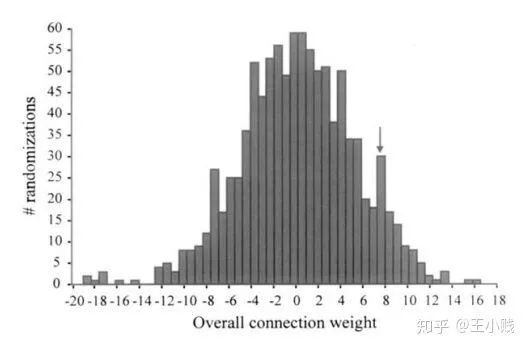
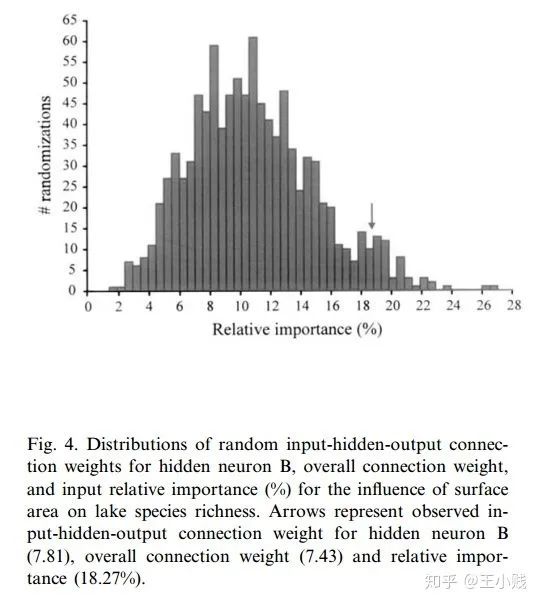
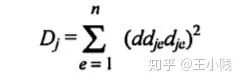
在网络训练终止后,将训练样本P中每一自变量特征在原值的基础上分别加/减10%后成两个训练样本P1和P2 将P1和P2分别作为仿真样本利用已建成的网络进行仿真,得到两个仿真结果A1和A2 求出A1和A2的差值,即为变动该自变量后对输出产生的影响变化值 最后将IV按观测样本数平均得到该自变量对应变量——网络输出的MIV。
2. 样本敏感性分析
 ,这样最后收敛的参数也会发生改变,然后得到参数的改变对
,这样最后收敛的参数也会发生改变,然后得到参数的改变对  的导数就是这个样本的影响力函数。
的导数就是这个样本的影响力函数。 是每个样本的损失函数,那么总的损失函数可以写成:
是每个样本的损失函数,那么总的损失函数可以写成: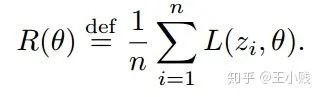
 的二阶偏导矩阵
的二阶偏导矩阵  可以写成下面的形式,这里我们假设
可以写成下面的形式,这里我们假设  是正定的,这样可以保证在后续推导中
是正定的,这样可以保证在后续推导中  的逆存在
的逆存在 ,这个时候可以得到一个新的收敛参数
,这个时候可以得到一个新的收敛参数 
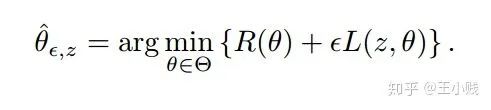
 ,则我们要计算的可以表示为:
,则我们要计算的可以表示为: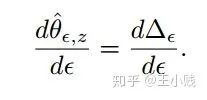
 趋近于0,
趋近于0, ,可以应用泰勒展开得到下面的式子
,可以应用泰勒展开得到下面的式子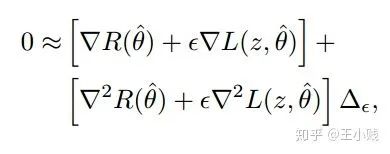
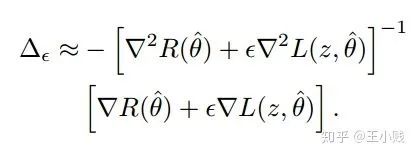
 ,只保留
,只保留  项
项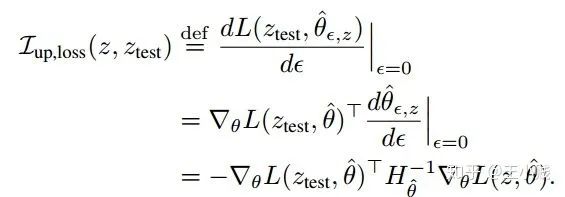
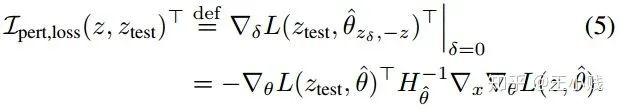


小结
关于BIGSCity
参考文献
[1] Google Brain, Interpretable Machine Learning: The fuss, the concrete and the questions.
[2] Kim B, Koyejo O, Khanna R, et al. Examples are not enough, learn to criticize! Criticism for Interpretability[C]. neural information processing systems, 2016: 2280-2288.
[3] Kim B, Rudin C, Shah J. The Bayesian Case Model: A Generative Approach for Case-Based Reasoning and Prototype Classification[J]. Computer Science, 2015, 3:1952-1960.
[4] Doshi-Velez F, Wallace B C, Adams R. Graph-sparse LDA: a topic model with structured sparsity[J]. Computer Science, 2014.
[5] Matthew D. Zeiler, Rob Fergus. Visualizing and Understanding Convolutional Networks[J]. 2013, 8689:818-833.
[6] David Bau, Bolei Zhou, Aditya Khosla, et al. Network Dissection: Quantifying Interpretability of Deep Visual Representations[J]. 2017:3319-3327.
[7] Yosinski J, Clune J, Bengio Y, et al. How transferable are features in deep neural networks?[J]. Eprint Arxiv, 2014, 27:3320-3328.
[8] Alain G, Bengio Y. Understanding intermediate layers using linear classifier probes[J]. 2016.
[9] Garson G D. Interpreting neural-network connection weights[M]. Miller Freeman, Inc. 1991.
[10] Olden J D, Jackson D A. Illuminating the “black box”: a randomization approach for understanding variable contributions in artificial neural networks[J]. Ecological Modelling, 2002, 154(1–2):135-150.
[11] Dimopoulos Y, Bourret P, Lek S. Use of some sensitivity criteria for choosing networks with good generalization ability[J]. Neural Processing Letters, 1995, 2(6):1-4.
[12] Koh P W, Liang P. Understanding Black-box Predictions via Influence Functions[J]. 2017.
苏航、纪荣嵘,陈熙霖等15位教授观点集锦:关于CV模型的可解释性的深入探讨|RACV2019
神经网络可解释性的另一种方法:积分梯度,解决梯度饱和缺陷
凭什么相信你,我的CNN模型?关于CNN模型可解释性的思考

