计算机视觉方向简介 | 多视角立体视觉MVS
点击上方“小白学视觉”,选择加"星标"或“置顶”
重磅干货,第一时间送达
知乎作者: 黄浴
多视角立体视觉(Multiple View Stereo,MVS)是对立体视觉的推广,能够在多个视角(从外向里)观察和获取景物的图像,并以此完成匹配和深度估计。某种意义上讲,SLAM/SFM其实和MVS是类似的,只是前者是摄像头运动,后者是多个摄像头视角。也可以说,前者可以在环境里面“穿行”,而后者更像在环境外“旁观”。
如图所示(a)-(d)是MVS方法的基本流程,不同的应用可能有各个主模块的不同实现,但总体方法是类似的:
•收集图像;
•针对每个图像计算相机参数;
•从图像集和相应的摄像机参数重建场景的3D几何图形;
•可选择地重建场景的形状和纹理颜色。
注:可以看出一些步骤和SLAM/SFM是类似的,算法也是互通可用。




尽管MVS与经典立体视觉算法具有相同的原理,但MVS算法旨在处理视角变化更多的图像,例如围绕目标拍摄的图像集,并且还处理甚至数百万数量的大量图像。MVS问题的差异最终会产生与经典立体视觉相应功能明显不同的算法。例如3D地图的工业应用,一次处理数百公里范围内数百万张照片,有效地重建大都市、国家乃至整个地球的场景。
与双目立体视觉法的分类思路相似,根据区分主要算法的六个基本属性对现有方法进行分类:场景表示,照片一致性(photo consistency)度量,可见性模型(visibility model),形状先验知识,重构算法以及初始化要求。
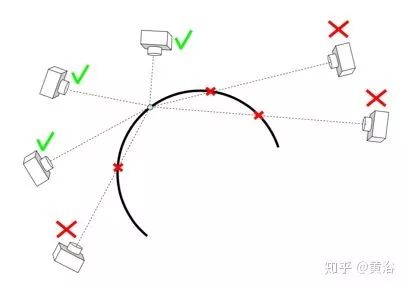
在初始化阶段,除了是一组标定图像之外,所有多视角立体视觉算法都假定或要求输入被重建的目标或场景的几何范围信息。
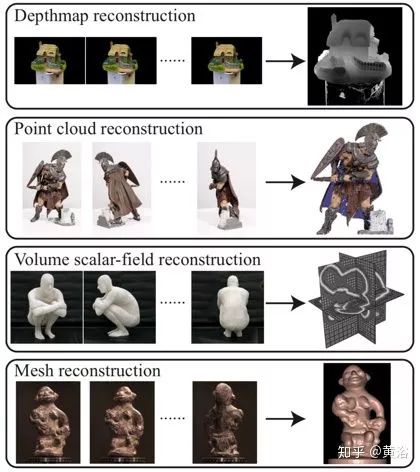
场景表示可以是体素、多边形网格、深度图和水平度集(level sets),如图是一些场景表示例子,即深度图,点云,体积标量场和网格。
图像一致性度量分为场景空间和图像空间两种,前者将几何点、面或体投影到图像并评估投影之间的相互协调度,后者基于场景几何估计变换(warp)来自一个视点的图像预测不同视点的图像然后计算预测图像和测量图像之间的预测误差。下图是两个图像像素一致性度量的例子,上面是纹理丰富,下面是纹理贫乏。

可见性模型(遮挡问题)确定在评估照片一致性度量时要考虑哪一个视角图像。由于场景可见度随视点变化,因此几乎所有MVS算法都会以某种方式解决这种遮挡问题。可见性技术包括几何、准几何和基于出格点等三种方法:几何法试图明确模拟图像形成过程和场景的形状,以确定哪些场景结构在哪些图像中是可见的;准几何技术使用近似几何推理来估计可见性关系;出格点法避免显式几何推理而是将遮挡视为出格点。下图是可见性问题示意图。
独立的照片一致性测量并不足以恢复精确的几何形状,特别是在低纹理场景区域。因此考虑偏向重建具有期望特性的形状先验知识可能是有帮助的。虽然先验知识对于立体视觉是必不可少的,但在多视图立体视觉中起着不太重要的作用,因为来自多视图的约束更强,比如表面积小的最小表面,以及体素着色(voxel coloring)和空间雕刻(space carving)方法采用的最大表面,还有可以放入马尔可夫随机场(MRF,Markov Random Field)的局部平滑性。
重建算法的划分有四类:
• 第一类方法首先在3D体积计算成本函数,然后从该体积提取表面进行操作,如体素着色算法及其变型,单次扫描体积计算成本并在扫描中重建所有低于成本阈值的体素;
• 第二类技术通过减少或最小化成本函数来迭代演化一个表面,此类方法包括基于体素、水平度集和曲面网格等;
• 第三类方法在图像空间计算一组深度图;
• 最后一类方法提取并匹配一组特征点然后曲面拟合重建的特征点。
基于MRF的图像一致性度量方法
下面以基于MRF的图像一致性度量方法为例介绍MVS的重建算法。
尽管可以使用强大的图像一致性函数,但在具有挑战性的场景中,一致性曲线的峰值可能与真实深度不对应。在严重遮挡的情况下,可能在大多数其他图像不存在匹配。一种标准解决方案是假设在相邻像素具有相似深度值的强制一致性,其中马尔可夫随机场(MRF)是用于该任务的非常流行且成功的模型。MRF深度图公式可以被视为组合优化问题,其中输入深度范围被离散化为有限的深度值集。而问题是将标签集的深度标签kp分配给每个像素p,最小化以下成本函数:
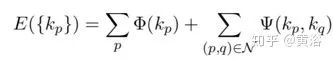
第一个求和项对图像的所有像素,而第二个求和项对所有相邻像素对。相邻像素通常通过4邻域或8邻域系统来定义。前者像素连接水平和垂直相邻像素。后者另外相邻的对角线像素也相互连接。4邻域系统具有较少的交互条件且更便宜,但可能受到离散化畸变的影响更大。
单元能量(Unary Potentials)
单元标签成本Φ(·)反映了图像一致性信息,其中成本应与图像一致性得分成反比,单元成本的确定义各不相同。但是,假设NCC是图像一致性函数的测度,其得分保证在[-1,1]范围内。那么单元成本可以定义为以下截断线性损失函数:
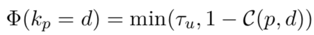
其中τu是截止阈值。当然,另一个任意的强大功能,例如Huber损失或Cauchy损失,可以代替使用。
成对交互能量(Pairwise Interaction Potentials)
成对成本强制空间正则化并被与相邻像素的深度差成比例,使得相邻像素具有相似的深度值。成对成本Ψ(·,·)的定义有所不同,下面是一个简单的实现:作为一个截断线性损失函数,避免过多地惩罚深度不连续性。
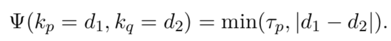
优化
上述MRF构造的重建问题通常是NP-hard问题,但是存在许多有效近似,特别是每对相邻像素的成对成本满足以下子模块条件
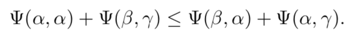
对于这个子模块函数,最流行的技术之一称为alpha-expansion,它反复解决最大流量最小切割(max-flow min- cut)算法以改进深度标签的分配。
幸运的是,子模块条件适用于许多标准成对项。更具体地说,作为距离度量,Ψ(α,α)应该是0,因为两个标签是相同的。然后,剩余的条件变成三角不等式:
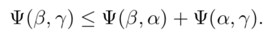
平滑的先验知识通常被定义为距离度量,并且满足该三角不等式。这种度量函数可以是线性、截断线性或Cauchy损失函数。但是,二次型或Huber损失函数不是子模块函数,因为二次函数不服从三角不等式。注意,与成对成本不同,单元能量没有限制,可以任意设定。
好消息,小白学视觉团队的知识星球开通啦,为了感谢大家的支持与厚爱,团队决定将价值149元的知识星球现时免费加入。各位小伙伴们要抓住机会哦!

交流群
欢迎加入公众号读者群一起和同行交流,目前有SLAM、三维视觉、传感器、自动驾驶、计算摄影、检测、分割、识别、医学影像、GAN、算法竞赛等微信群(以后会逐渐细分),请扫描下面微信号加群,备注:”昵称+学校/公司+研究方向“,例如:”张三 + 上海交大 + 视觉SLAM“。请按照格式备注,否则不予通过。添加成功后会根据研究方向邀请进入相关微信群。请勿在群内发送广告,否则会请出群,谢谢理解~

