在模仿中精进数据可视化03:OD数据的特殊可视化方式

点击上方"蓝字"关注我们
记录 分享 成长
❝本文完整代码及数据已上传至我的
❞Github仓库https://github.com/CNFeffery/FefferyViz
1 简介
「OD数据」是交通、城市规划以及GIS等领域常见的一类数据,特点是每一条数据都记录了一次OD(O即Origin,D即Destination)行为的起点与终点坐标信息。
而针对「OD数据」常见的可视化表达方式为弧线图,譬如图1所示的例子,就针对纽约曼哈顿等区域的某时间段「Uber」打车记录上下车点数据进行展示:
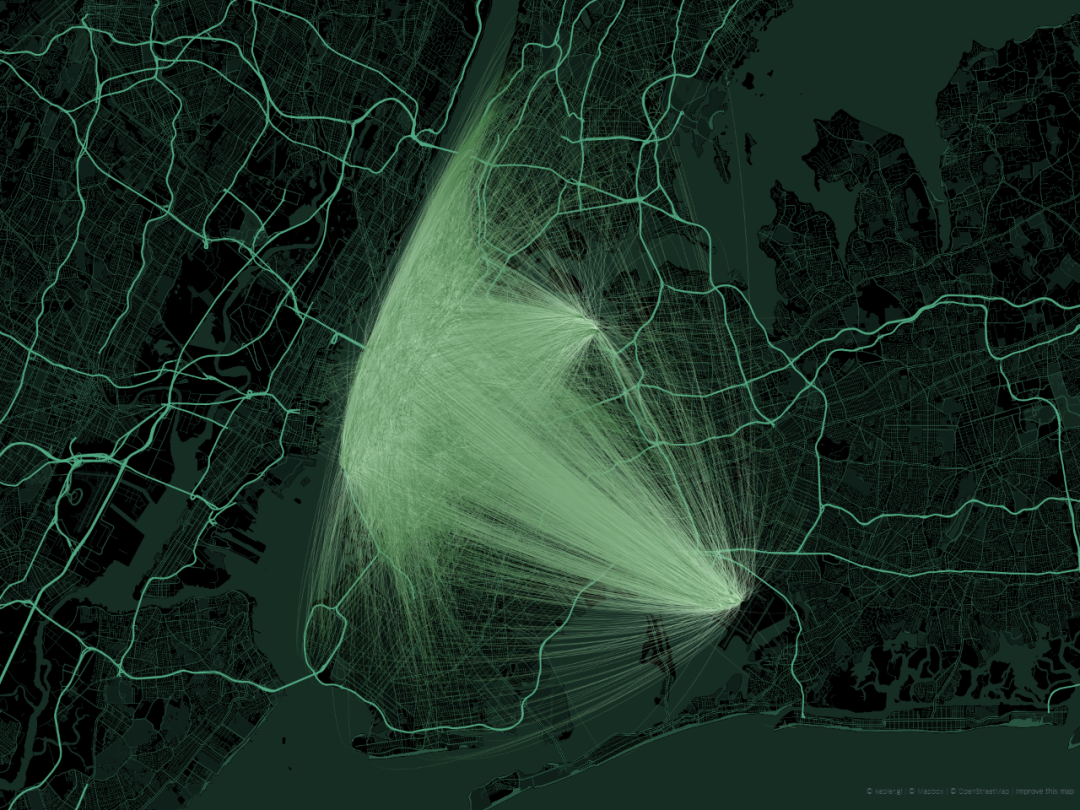
但这种传统的表达方式局限很明显:当OD记录数量众多时,因为不同线之间的彼此堆叠,导致很多区域之间的OD模式被遮盖而难以被读出。
而前一段时间我在观看一场学术直播的过程中,注意到一种特别的表达区域间OD数据的方式,原始文献比较老( https://openaccess.city.ac.uk/id/eprint/537/1/wood_visualization_2010.pdf )发表于2010年,其思想是通过对研究区域进行网格化划分,再将整个区域的原始网格映射到每个单一网格中:
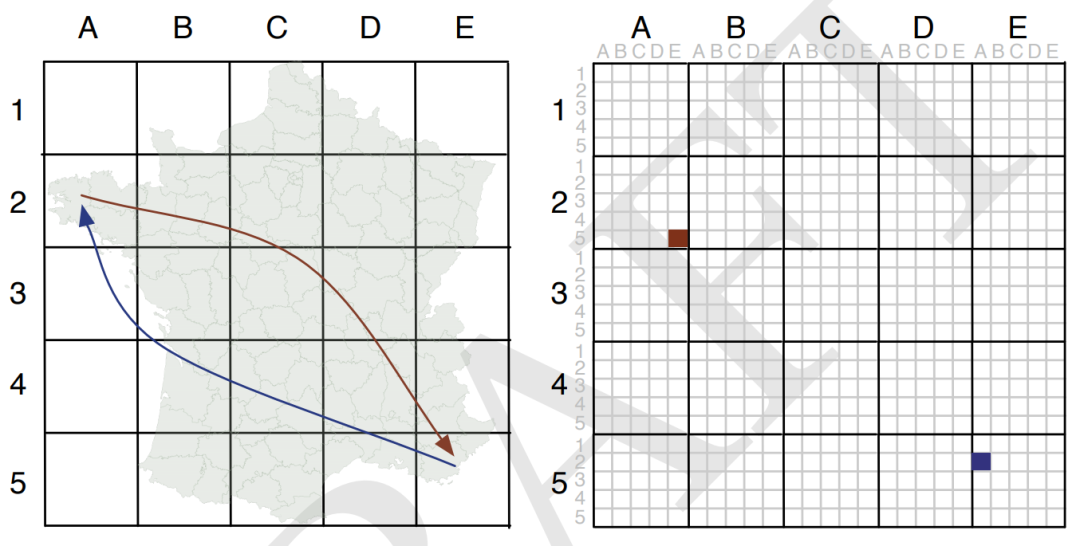
譬如图2左图中从坐标记为的网格出发,到达记为的网格的所有OD数据记录,可以在右图中对应左图位置的大网格中,划分出的对应相对位置的小网格中进行记录。
通过这样的方式,原始文献将图3所示原始OD线图转换为图4:
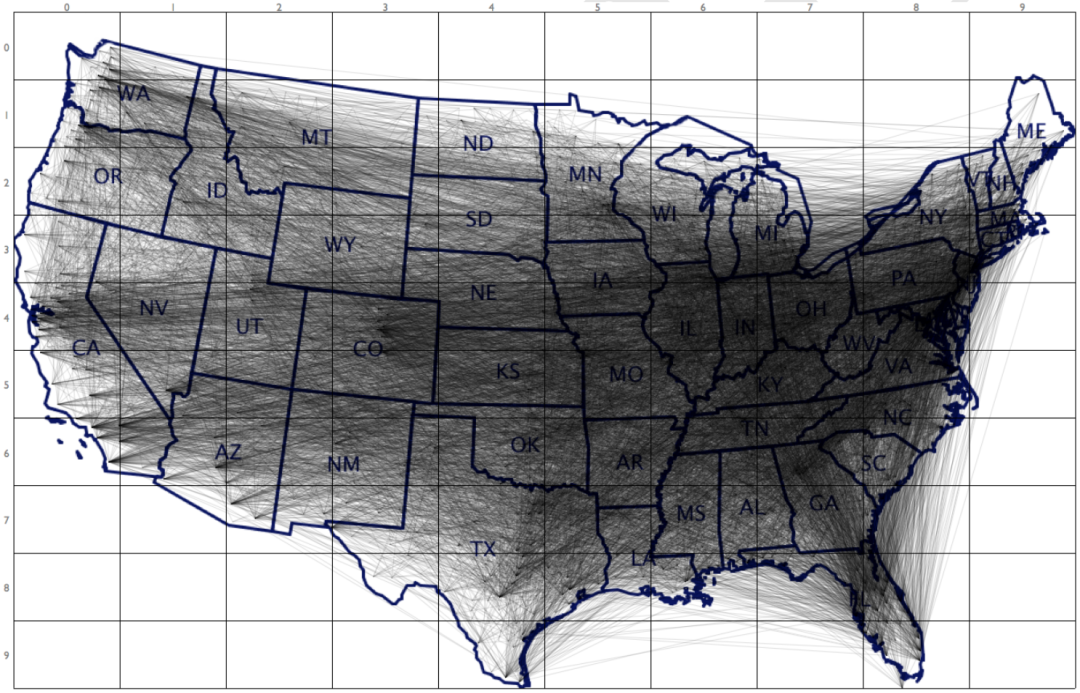
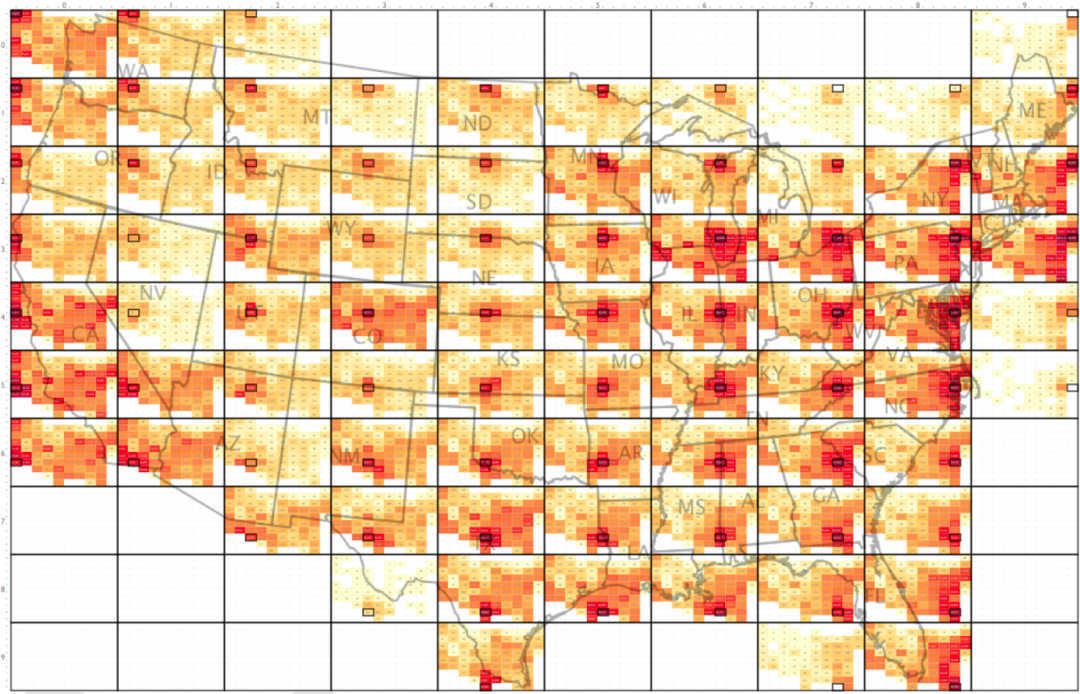
使得我们可以非常清楚地观察到每个网格区域对其他网格区域的OD模式,而本文就将利用Python,在图1对应的「Uber」上下车点分布数据的基础上,实践这种表达OD数据的特别方式。
2 模仿过程
2.1 过程分解
首先我们需要梳理一下整体的逻辑,先来看看原始的数据:
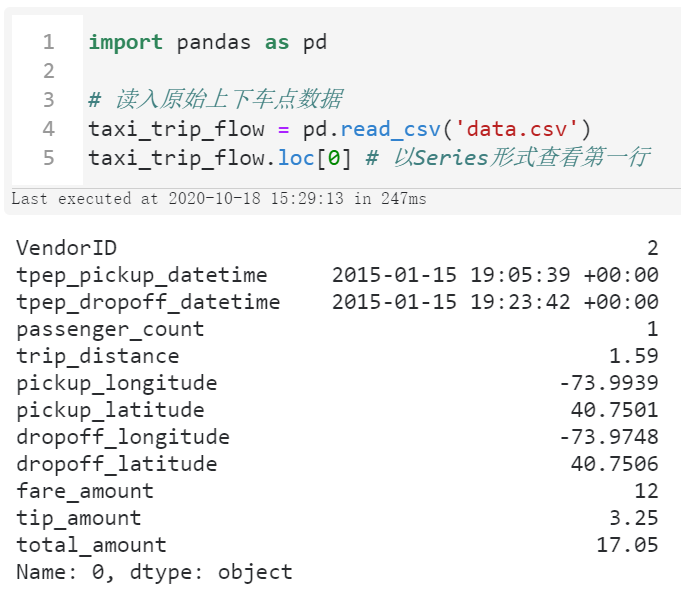
可以看到,原始数据中我们在本文真正用得到字段为上车点经纬度pickup_longitude与pickup_latitude,以及下车点经纬度dropoff_longitude与dropoff_latitude。
我的思路是首先对所有经纬度点进行去重,接着保存为GeoDataFrame并统一坐标参考系为「Web墨卡托」也就是EPSG:3857:
from shapely.geometry import Point
import geopandas as gpd
od_points = \
(
# 首先合并所有的经纬度信息
pd
.concat([taxi_trip_flow[['pickup_longitude', 'pickup_latitude']]
.rename(columns={'pickup_longitude': 'lng',
'pickup_latitude': 'lat'}),
taxi_trip_flow[['dropoff_longitude', 'dropoff_latitude']]
.rename(columns={'dropoff_longitude': 'lng',
'dropoff_latitude': 'lat'})])
# 对经纬度进行去重
.drop_duplicates()
)
# 基于经纬度信息为od_points添加矢量信息列
od_points['geometry'] = (
od_points
.apply(lambda row: Point(row['lng'], row['lat']), axis=1)
)
# 转换为GeoDataFrame并统一坐标到Web墨卡托
od_points = gpd.GeoDataFrame(od_points, crs='EPSG:4326').to_crs('EPSG:3857')
od_points.head()
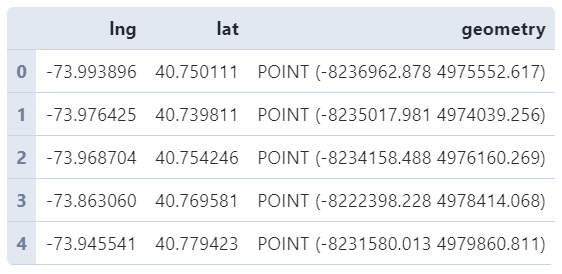
接下来我们来为研究区域创建网格面矢量数据,思路是利用numpy先创建出x和y方向上的等间距坐标,譬如我们这里创建5行5列:
from shapely.geometry import MultiLineString
from shapely.ops import polygonize # 用于将交叉线转换为网格面
# 提取所有上下车坐标点范围的左下角及右上角坐标信息
xmin, ymin, xmax, ymax = od_points.total_bounds
# 创建x方向上的所有坐标位置
x = np.linspace(xmin,
xmax,
6)
# 创建y方向上的所有坐标位置
y = np.linspace(ymin,
ymax,
6)
再利用双层列表推导配合MultiLineString生成彼此交叉的网格线,并利用shapely中提供的polygonize工具直接把交叉线转换为MultiPolygon,再拆分每个单一网格并添加一一对应的id信息以方便之后的分析过程。
# 生成全部交叉线坐标信息
hlines = [((x1, yi), (x2, yi)) for x1, x2 in zip(x[:-1], x[1:]) for yi in y]
vlines = [((xi, y1), (xi, y2)) for y1, y2 in zip(y[:-1], y[1:]) for xi in x]
# 创建网格
manhattan_grids = gpd.GeoDataFrame({
'geometry': list(polygonize(MultiLineString(hlines + vlines)))},
crs='EPSG:3857')
# 添加一一对应得id信息
manhattan_grids['id'] = manhattan_grids.index
上面的创建网格的方法非常实用,爱学习的朋友的可以仔细看懂之后记录下来。
我们来简单看看创建出的网格是什么样子的,配合contextily添加上在线底图:
import matplotlib.pyplot as plt
import contextily as ctx
fig, ax = plt.subplots(figsize=(4, 4), dpi=200)
ax = manhattan_grids.plot(facecolor='none', edgecolor='black', ax=ax)
# 标注每个网格的id
for row in manhattan_grids.itertuples():
centroid = row.geometry.centroid
ax.text(centroid.x, centroid.y, row.id, ha='center', va='center')
# 关闭坐标轴
ax.axis('off')
# 添加carto的素色底图
ctx.add_basemap(ax,
source='https://d.basemaps.cartocdn.com/light_nolabels/{z}/{x}/{y}.png',
zoom=12)
fig.savefig('图7.png', dpi=300, bbox_inches='tight', pad_inches=0)
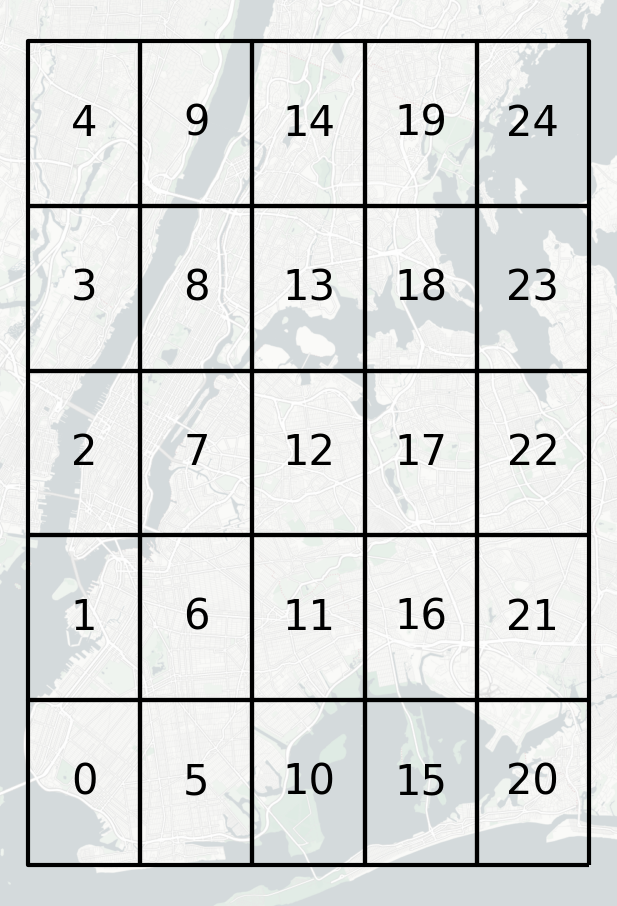
创建出的网格效果不错~接下来就到了最关键的地方,我们需要计算出在每个原始网格内部上车的全部OD记录,在整个区域中各个网格内的下车点分布情况:
首先我们以某个网格为例,介绍如何为其关联上车点、下车点信息,并利用简单的仿射变换得到镶嵌在其内部的小网格。
以id=21的网格为例,对应着肯尼迪国际机场的区域,首先我们利用id对应的从manhattan_grids表中提取的网格面数据,基于空间连接来与od_points表进行关联,从而匹配到目标网格内对应原始od信息表中的所有上车点记录;
接着根据这些记录对应的下车点信息与od_points表进行匹配,从而得到所有下车点矢量信息,然后再次利用空间连接,得到所需的网格下车点分布结果:
i = 21 # 对应肯尼迪国际机场的网格
# 计算得到所有网格整体的重心坐标
center_grid = (manhattan_grids.unary_union.centroid.x,
manhattan_grids.unary_union.centroid.y)
# 提取对应下车点坐标
dropoff = (
# 利用空间连接,提取目标网格中包含到的所有坐标点
gpd
.sjoin(manhattan_grids.loc[i:i, :],
right_df=od_points,
op='contains')
[['lng', 'lat', 'geometry']]
# 利用提取到的坐标点信息,关联在目标
# 网格中上车的记录对应的下车点坐标
.merge(taxi_trip_flow[['pickup_longitude',
'pickup_latitude',
'dropoff_longitude',
'dropoff_latitude']],
left_on=['lng', 'lat'],
right_on=['pickup_longitude',
'pickup_latitude'])
[['dropoff_longitude', 'dropoff_latitude']]
# 根据匹配到的下车点坐标
# 与od_points表进行连接
# 找到对应下车点的矢量信息
.merge(od_points,
left_on=['dropoff_longitude', 'dropoff_latitude'],
right_on=['lng', 'lat'])[['geometry']]
)
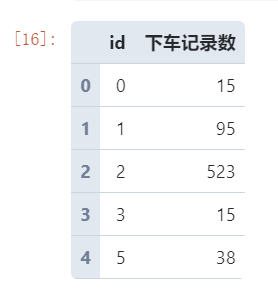
# 提取上一步得到的下车坐标点在各个网格中的分布数据
grid_distrib = (
# 利用空间连接匹配网格与下车坐标点
gpd
.sjoin(manhattan_grids,
# 转换为同一坐标参考系的GeoDataFrame
gpd.GeoDataFrame(dropoff, crs='EPSG:3857'),
op='contains')
# 根据网格id进行分组计数
.groupby('id', as_index=False)
.agg({'index_right': 'count'})
.rename(columns={'index_right': '下车记录数'})
)
grid_distrib.head()
接着我们将上述的统计结果按照id列与原始网格表进行关联,并利用仿射变换得到整体网格向目标网格内部的缩小镶嵌结果(思路是首先将原始网格整体移动到与目标网格重心重合,接着按照x和y方向上的比例进行缩小),为了方便之后绘图标记出目标网格对应的镶嵌小网格位置,最后还需添加是否为目标网格列信息:
# 利用基本的仿射变换得到原始网格向对应目标网格的嵌入变换
# 获取当前目标网格的重心坐标
center_child_grid = (manhattan_grids.at[i, 'geometry'].centroid.x,
manhattan_grids.at[i, 'geometry'].centroid.y)
# 利用仿射变换得到整体网格在目标网格中的镶嵌
draw_gdf = (
manhattan_grids
# 基于原始的网格矢量来更新放缩后的网格矢量
.assign(geometry=manhattan_grids
# 第一步:将原始网格的重心平移到目标网格的重心上
.translate(center_child_grid[0]-center_grid[0],
center_child_grid[1]-center_grid[1])
# 第二步:以目标网格的重心为缩放中心,进行
.scale(xfact=1 / 5, yfact=1 / 5,
origin=(manhattan_grids.at[i, 'geometry'].centroid.x,
manhattan_grids.at[i, 'geometry'].centroid.y)))
.merge(grid_distrib, on='id', how='left')
.assign(是否为目标网格=0)
)
draw_gdf.loc[draw_gdf.id == i, '是否为目标网格'] = 1
draw_gdf.head()
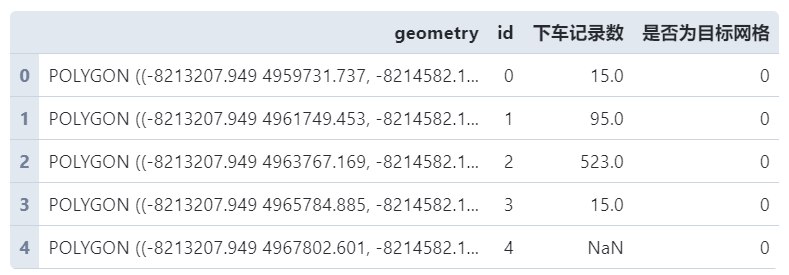
经过这一系列操作,我们就得到了id为21的网格下车点分布结果,将上述过程利用循环推广到每个网格,并将最后的计算结果合并为一张GeoDataFrame,即表draw_base。
2.2 绘制图像
最终我们对draw_base表进行可视化,这里为了显示更加自然,对下车记录进行了「对数化」+「自然间断」处理:
%matplotlib inline
fig, ax = plt.subplots(figsize=(12, 12))
# 绘制每个镶嵌小网格的轮廓
ax = (
draw_base
.plot(facecolor='none', edgecolor='lightgrey', ax=ax,
linewidth=0.3)
)
# 绘制每个镶嵌小网格的下车记录数热力分布
ax = (
draw_base
.assign(下车记录数=np.log(draw_base.下车记录数))
.plot(column='下车记录数', scheme='NaturalBreaks',
k=5, cmap='YlOrRd', ax=ax, alpha=0.7)
)
# 绘制原始网格的框架
ax = manhattan_grids.plot(ax=ax, facecolor='none', edgecolor='black',
linewidth=0.8)
# 在每个原始网格中标记出对应位置的镶嵌小网格
ax = (
draw_base
.query('是否为目标网格 == 1')
.plot(facecolor='none', edgecolor='black',
linestyle='--', ax=ax)
)
# 设置绘图区域范围
minx, miny, maxx, maxy = manhattan_grids.total_bounds
ax.set_xlim(minx, maxx)
ax.set_ylim(miny, maxy)
# 关闭坐标轴
ax.axis('off')
# 添加在线底图
ctx.add_basemap(ax,
source='https://d.basemaps.cartocdn.com/light_nolabels/{z}/{x}/{y}.png',
zoom=12)
# 保存图像
fig.savefig('图10.png', dpi=500, bbox_inches='tight', pad_inches=0)
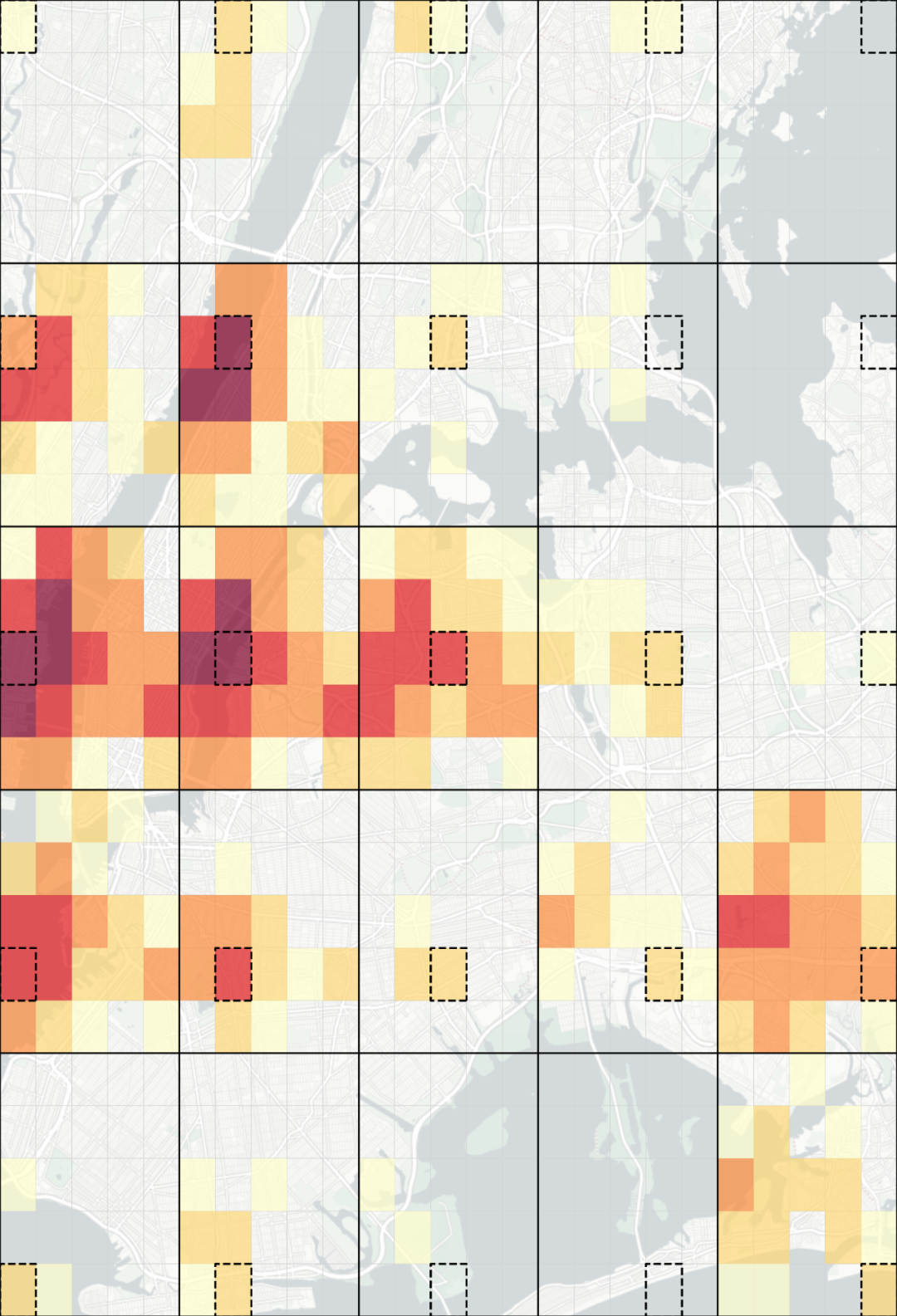
通过这种表达方式,我们可以很明显地看出不同区域相对其他区域出行模式的不同,你还可以根据自己的需要,对上述绘图逻辑进行调整,譬如每个原始网格内部色彩独立映射等。
以上就是本文的全部内容,欢迎在评论区与我进行讨论~
我们的知识星球【Python大数据分析】
限时优惠中!扫码领券
年费立减20,仅需59元~
快来一起玩转数据分析吧???
Python大数据分析
data creates value
扫码关注我们

