Python数据科学:史上最全的Numpy计算函数总结,建议收藏!

点击上方 蓝字 关注我们


Numpy提供了灵活的、静态类型的、可编译的程序接口口来优化数组的计算,也被称作向量操作,因此在Python数据科学界Numpy显得尤为重要。Numpy的向量操作是通过通用函数实现的。今天小编会给大家较为全面地介绍下Numpy的通用函数。
01
数组的运算
Numpy通用函数涉及到Python原生的算术运算符,标准的加减乘除都可以使用,同时这些运算符也是Numpy内置函数的简单封装器,例如“+”就是add函数的封装器。下图汇总了Numpy实现的算术运算符。
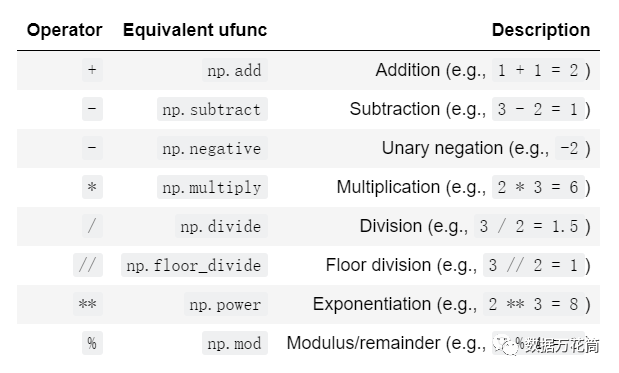
Numpy的加减乘除运算
x = np.arange(4)print("x =", x)print("x + 5 =", x + 5)print("x - 5 =", x - 5)print("x * 2 =", x * 2)print("x / 2 =", x / 2)print("x // 2 =", x // 2) # 向下整除# x = [0 1 2 3]# x + 5 = [5 6 7 8]# x - 5 = [-5 -4 -3 -2]# x * 2 = [0 2 4 6]# x / 2 = [ 0. 0.5 1. 1.5]# x // 2 = [0 0 1 1]
求负数、**表示求指数运算符以及%表示求%运算符,请看下面示例:
print("-x = ", -x)print("x ** 2 = ", x ** 2)print("x % 2 = ", x % 2)# -x = [ 0 -1 -2 -3]# x ** 2 = [0 1 4 9]# x % 2 = [0 1 0 1]
如果多个运算符组合使用时,需要考虑这些运算符的一个优先级。
-(0.5*x + 1) ** 2# array([-1. , -2.25, -4. , -6.25])
使用封装函数计算标准的加减乘除。
np.add(x, 2)
02
绝对值
Numpy通用的绝对值函数是np.absolute,也可以用其别名来访问np.abs。这个通用函数也可以处理复数,处理复数时,绝对值返回的是该复数的模。
x = np.array([-2, -1, 0, 1, 2])abs(x)# array([2, 1, 0, 1, 2])np.absolute(x)# array([2, 1, 0, 1, 2])np.abs(x)# array([2, 1, 0, 1, 2])x = np.array([3 - 4j, 4 - 3j, 2 + 0j, 0 + 1j])np.abs(x)# array([ 5., 5., 2., 1.])
03
三角函数
三角函数是数据科学中常用到的函数,这里会讲解三角函数的计算以及逆三角函数的计算。
首先,我们需要先定义一个角度数组,然后通过cos(),sin(),tan()等三角函数进行计算。
theta = np.linspace(0, np.pi, 3)print("theta = ", theta)print("sin(theta) = ", np.sin(theta))print("cos(theta) = ", np.cos(theta))print("tan(theta) = ", np.tan(theta))# theta = [ 0. 1.57079633 3.14159265]# sin(theta) = [ 0.00000000e+00 1.00000000e+00 1.22464680e-16]# cos(theta) = [ 1.00000000e+00 6.12323400e-17 -1.00000000e+00]# tan(theta) = [ 0.00000000e+00 1.63312394e+16 -1.22464680e-16]
同样我们也可以计算逆三角函数。
x = [-1, 0, 1]print("x = ", x)print("arcsin(x) = ", np.arcsin(x))print("arccos(x) = ", np.arccos(x))print("arctan(x) = ", np.arctan(x))# x = [-1, 0, 1]# arcsin(x) = [-1.57079633 0. 1.57079633]# arccos(x) = [ 3.14159265 1.57079633 0. ]# arctan(x) = [-0.78539816 0. 0.78539816]
04
指数和对数
Numpy中的指数运算。
x = [1, 2, 3]print("x =", x)print("e^x =", np.exp(x))print("2^x =", np.exp2(x))print("3^x =", np.power(3, x))# x = [1, 2, 3]# e^x = [ 2.71828183 7.3890561 20.08553692]# 2^x = [ 2. 4. 8.]# 3^x = [ 3 9 27
Numpy中的对数运算。
对数运算是指数运算的逆运算,最基础的np.log是以自然对数为底数的对数,同时也可以使用np.log2,np.log10等计算以2或10为底的对数。
x = [1, 2, 4, 10]print("x =", x)print("ln(x) =", np.log(x))print("log2(x) =", np.log2(x))print("log10(x) =", np.log10(x))# x = [1, 2, 4, 10]# ln(x) = [ 0. 0.69314718 1.38629436 2.30258509]# log2(x) = [ 0. 1. 2. 3.32192809]# log10(x) = [ 0. 0.30103 0.60205999 1. ]
特殊情况下,对于非常小的输入值可以保持较好的精度。当x很小时,以下函数给出的值np.log和np.exp的计算更加精确。
x = [0, 0.001, 0.01, 0.1]print("exp(x) - 1 =", np.expm1(x))print("log(1 + x) =", np.log1p(x))# exp(x) - 1 = [ 0. 0.0010005 0.01005017 0.10517092]# log(1 + x) = [ 0. 0.0009995 0.00995033 0.09531018]
05
专用的通用函数
Numpy还提供了很多通用函数,包括了双曲三角函数,比特位运算,比较运算符,弧度转化为角度的运算,取整和求余运算。除此之外呢,Python中还有更加专用的通用函数模块scipy.special,下面会为大家展示一部分的代码片段。
Gamma函数(广义阶乘,generlized factorials)和相关函数
from scipy import specialx = [1, 5, 10]print("gamma(x) =", special.gamma(x))print("ln|gamma(x)| =", special.gammaln(x))print("beta(x, 2) =", special.beta(x, 2))# gamma(x) = [ 1.00000000e+00 2.40000000e+01 3.62880000e+05]# ln|gamma(x)| = [ 0. 3.17805383 12.80182748]# beta(x, 2) = [ 0.5 0.03333333 0.00909091]
误差函数(高斯积分)
高斯积分的实现和逆实现
# Error function (integral of Gaussian)# its complement, and its inversex = np.array([0, 0.3, 0.7, 1.0])print("erf(x) =", special.erf(x))print("erfc(x) =", special.erfc(x))print("erfinv(x) =", special.erfinv(x))# erf(x) = [ 0. 0.32862676 0.67780119 0.84270079]# erfc(x) = [ 1. 0.67137324 0.32219881 0.15729921]# erfinv(x) = [ 0. 0.27246271 0.73286908 inf]
06
指定输出
所有的通用函数都可以通过out参数来指定计算结果的存放位置。
x = np.arange(5)y = np.empty(5)np.multiply(x, 10, out=y)print(y)# [ 0. 10. 20. 30. 40.]
这个特性也可以被称为数组视图,例如将计算结果写入指定数组的每隔一个元素的位置。
y = np.zeros(10)np.power(2, x, out=y[::2])print(y)# [ 1. 0. 2. 0. 4. 0. 8. 0. 16. 0.]
07
聚合
我们希望用一个特定的运算reduce一个数组,那么可以用任何通用函数的reduce方法。一个reduce方法会对给定元素和操作重复执行,直到得到这个结果。
对add通用函数调用reduce方法会返回数组中所有元素的和。
x = np.arange(1, 6)np.add.reduce(x)# 15
对multiply通用函数调用reduce方法会返回数组中所有元素的乘积。
np.multiply.reduce(x)# 120
accumulate函数可以储存每次计算的中间结果表。
np.add.accumulate(x)# array([ 1, 3, 6, 10, 15]
np.multiply.accumulate(x)array([ 1, 2, 6, 24, 120])# array([ 1, 2, 6, 24, 120])
任何通用函数都可以用outer方法获得两个不同输入数组所有元素对函数运算的结果。这意味着一行代码实现一个乘法表。
通用函数还能够操纵形状和大小不一样的数组,一组这样的操作被称为广播,后面会细讲。
x = np.arange(1, 6)np.multiply.outer(x, x)# array([[ 1, 2, 3, 4, 5],# [ 2, 4, 6, 8, 10],# [ 3, 6, 9, 12, 15],# [ 4, 8, 12, 16, 20],# [ 5, 10, 15, 20, 25]])
相关阅读:
