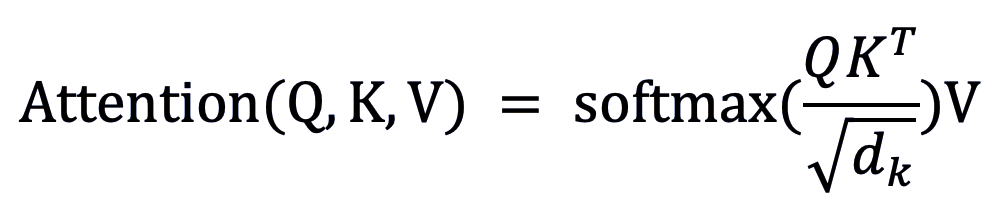​Numpy手写机器学习算法，3万行代码！

点击下方卡片，关注“新机器视觉”公众号
重磅干货，第一时间送达

转自：机器之心

NumPy 作为 Python 生态中最受欢迎的科学计算包，很多读者已经非常熟悉它了。

它为 Python 提供高效率的多维数组计算，并提供了一系列高等数学函数，我们可以快速搭建模型的整个计算流程。毫不负责任地说，NumPy 就是现代深度学习框架的「爸爸」。

尽管目前使用 NumPy 写模型已经不是主流，但这种方式依然不失为是理解底层架构和深度学习原理的好方法。最近，来自普林斯顿的一位博士后将 NumPy 实现的所有机器学习模型全部开源，超过 3 万行代码、30 多个模型，并提供了相应的论文和一些实现的测试效果。

项目地址：https://github.com/ddbourgin/numpy-ml

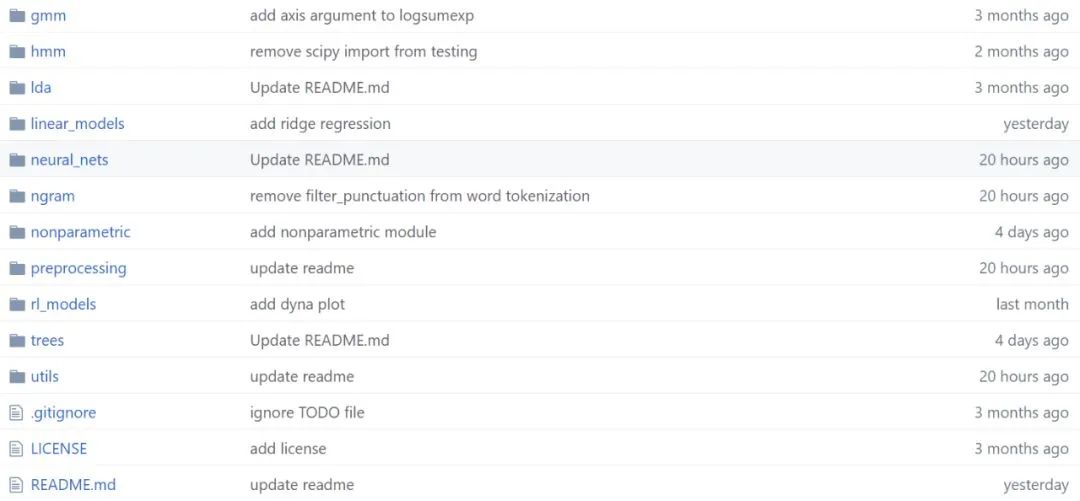
粗略估计，该项目大约有 30 个主要机器学习模型，此外还有 15 个用于预处理和计算的小工具，全部.py 文件数量有 62 个之多。平均每个模型的代码行数在 500 行以上，在神经网络模型的 layer.py 文件中，代码行数接近 4000。

这，应该是目前用 NumPy 手写机器学习模型的「最高境界」吧。
谁用 NumPy 手推了一大波 ML 模型？
通过项目的代码目录，我们能发现，作者基本上把主流模型都实现了一遍，这个工作量简直惊为天人。作者 David Bourgin 是一位大神，于 2018 年获得加州大学伯克利分校计算认知科学博士学位，随后在普林斯顿大学从事博士后研究。

尽管毕业不久，David 在顶级期刊与计算机会议上都发表了一些优秀论文。在 ICML 2019 中，其关于认知模型先验的研究就被接收为少有的 Oral 论文。


David Bourgin 就是用 NumPy 手写 ML 模型、手推反向传播的大神。这么多的工作量，当然还是需要很多参考资源的，David 会理解这些资源或实现，并以一种更易读的方式写出来。

他表示，从 autograd repo 学到了很多，但二者的不同之处在于，他显式地进行了所有梯度计算，以突出概念/数学的清晰性。当然，这么做的缺点也很明显，在每次需要微分一个新函数时，你都要写出它的公式……

估计 David Bourgin 在写完这个项目后，机器学习基础已经极其牢固了。
项目总体介绍
这个项目最大的特点是作者把机器学习模型都用 NumPy 手写了一遍，包括更显式的梯度计算和反向传播过程。可以说它就是一个机器学习框架了，只不过代码可读性会强很多。

David Bourgin 表示他一直在慢慢写或收集不同模型与模块的纯 NumPy 实现，它们跑起来可能没那么快，但是模型的具体过程一定足够直观。每当我们想了解模型 API 背后的实现，却又不想看复杂的框架代码，那么它可以作为快速的参考。

文章后面会具体介绍整个项目都有什么模型，这里先简要介绍它的整体结构。如下所示为项目文件，不同的文件夹即不同种类的代码集。


在每一个代码集下，作者都会提供不同实现的参考资料，例如模型的效果示例图、参考论文和参考链接等。如下所示，David 在实现神经网络层级的过程中，还提供了参考论文。


当然如此庞大的代码总会存在一些 Bug，作者也非常希望我们能一起完善这些实现。如果我们以前用纯 NumPy 实现过某些好玩的模型，那也可以直接提交 PR 请求。因为实现基本上都只依赖于 NumPy，那么环境配置就简单很多了，大家差不多都能跑得动。
手写 NumPy 全家福
作者在 GitHub 中提供了模型/模块的实现列表，列表结构基本就是代码文件的结构了。整体上，模型主要分为两部分，即传统机器学习模型与主流的深度学习模型。

其中浅层模型既有隐马尔可夫模型和提升方法这样的复杂模型，也包含了线性回归或最近邻等经典方法。而深度模型则主要从各种模块、层级、损失函数、最优化器等角度搭建代码架构，从而能快速构建各种神经网络。

除了模型外，整个项目还有一些辅助模块，包括一堆预处理相关的组件和有用的小工具。

该 repo 的模型或代码结构如下所示：

1. 高斯混合模型
EM 训练
2. 隐马尔可夫模型
维特比解码
似然计算
通过 Baum-Welch/forward-backward 算法进行 MLE 参数估计
3. 隐狄利克雷分配模型（主题模型）
用变分 EM 进行 MLE 参数估计的标准模型
用 MCMC 进行 MAP 参数估计的平滑模型
4. 神经网络
4.1 层/层级运算
Add
Flatten
Multiply
Softmax
全连接/Dense
稀疏进化连接
LSTM
Elman 风格的 RNN
最大+平均池化
点积注意力
受限玻尔兹曼机 (w. CD-n training)
2D 转置卷积 (w. padding 和 stride)
2D 卷积 (w. padding、dilation 和 stride)
1D 卷积 (w. padding、dilation、stride 和 causality)
4.2 模块
双向 LSTM
ResNet 风格的残差块（恒等变换和卷积）
WaveNet 风格的残差块（带有扩张因果卷积）
Transformer 风格的多头缩放点积注意力
4.3 正则化项
Dropout
归一化
批归一化（时间上和空间上）
层归一化（时间上和空间上）
4.4 优化器
SGD w/ 动量
AdaGrad
RMSProp
Adam
4.5 学习率调度器
常数
指数
Noam/Transformer
Dlib 调度器
4.6 权重初始化器
Glorot/Xavier uniform 和 normal
He/Kaiming uniform 和 normal
标准和截断正态分布初始化
4.7 损失
交叉熵
平方差
Bernoulli VAE 损失
带有梯度惩罚的 Wasserstein 损失
4.8 激活函数
ReLU
Tanh
Affine
Sigmoid
Leaky ReLU
4.9 模型
Bernoulli 变分自编码器
带有梯度惩罚的 Wasserstein GAN
4.10 神经网络工具
col2im (MATLAB 端口)
im2col (MATLAB 端口)
conv1D
conv2D
deconv2D
minibatch
5. 基于树的模型
决策树 (CART)
[Bagging] 随机森林
[Boosting] 梯度提升决策树
6. 线性模型
岭回归
Logistic 回归
最小二乘法
贝叶斯线性回归 w/共轭先验
7.n 元序列模型
最大似然得分
Additive/Lidstone 平滑
简单 Good-Turing 平滑
8. 强化学习模型
使用交叉熵方法的智能体
首次访问 on-policy 蒙特卡罗智能体
加权增量重要采样蒙特卡罗智能体
Expected SARSA 智能体
TD-0 Q-learning 智能体
Dyna-Q / Dyna-Q+ 优先扫描
9. 非参数模型
Nadaraya-Watson 核回归
k 最近邻分类与回归
10. 预处理
离散傅立叶变换 (1D 信号)
双线性插值 (2D 信号)
最近邻插值 (1D 和 2D 信号)
自相关 (1D 信号）
信号窗口
文本分词
特征哈希
特征标准化
One-hot 编码/解码
Huffman 编码/解码
词频逆文档频率编码
11. 工具
相似度核
距离度量
优先级队列
Ball tree 数据结构
项目示例
由于代码量庞大，这里整理了一些示例。

例如，实现点积注意力机制：
class DotProductAttention(LayerBase):
    def __init__(self, scale=True, dropout_p=0, init="glorot_uniform", optimizer=None):
        super().__init__(optimizer)
        self.init = init
        self.scale = scale
        self.dropout_p = dropout_p
        self.optimizer = self.optimizer
        self._init_params()

    def _fwd(self, Q, K, V):
        scale = 1 / np.sqrt(Q.shape[-1]) if self.scale else 1
        scores = Q @ K.swapaxes(-2, -1) * scale  # attention scores
        weights = self.softmax.forward(scores)  # attention weights
        Y = weights @ V
        return Y, weights

    def _bwd(self, dy, q, k, v, weights):
        d_k = k.shape[-1]
        scale = 1 / np.sqrt(d_k) if self.scale else 1

        dV = weights.swapaxes(-2, -1) @ dy
        dWeights = dy @ v.swapaxes(-2, -1)
        dScores = self.softmax.backward(dWeights)
        dQ = dScores @ k * scale
        dK = dScores.swapaxes(-2, -1) @ q * scale
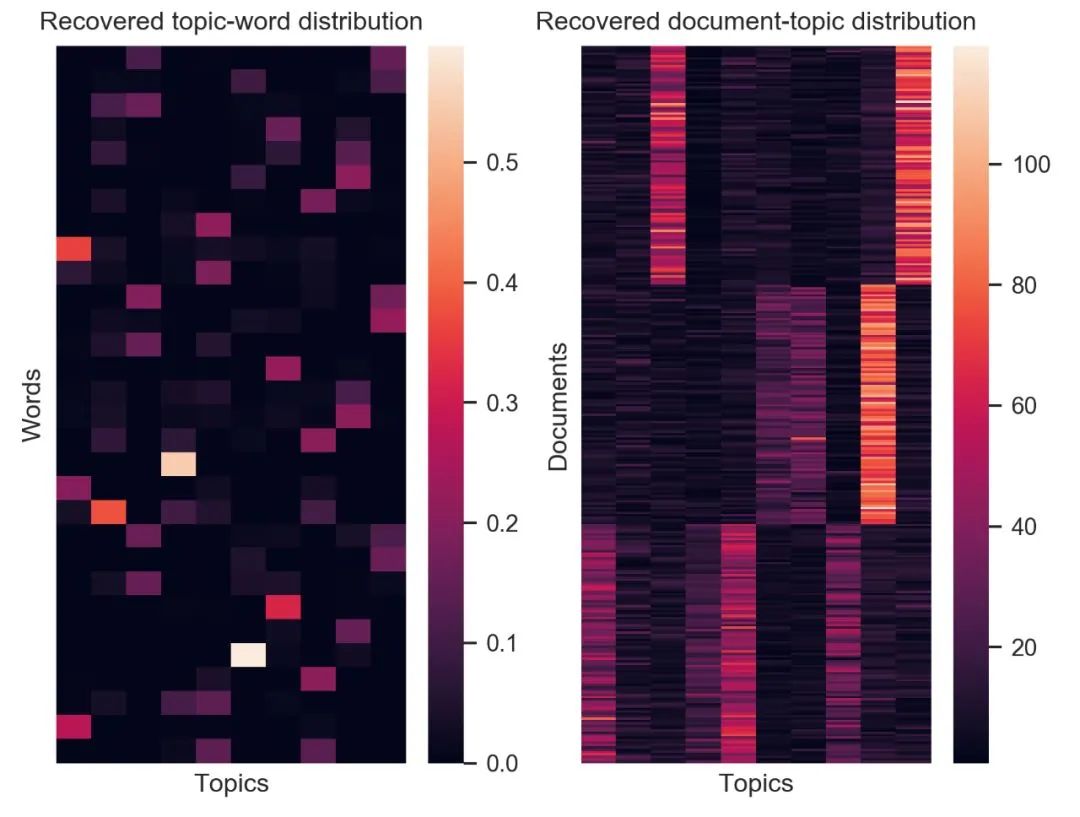
        return dQ, dK, dV

在以上代码中，Q、K、V 三个向量输入到「_fwd」函数中，用于计算每个向量的注意力分数，并通过 softmax 的方式得到权重。而「_bwd」函数则计算 V、注意力权重、注意力分数、Q 和 K 的梯度，用于更新网络权重。

在一些实现中，作者也进行了测试，并给出了测试结果。如图为隐狄利克雷（Latent Dirichlet allocation，LDA）实现进行文本聚类的结果。左图为词语在特定主题中的分布热力图。右图则为文档在特定主题中的分布热力图。

图注：隐狄利克雷分布实现的效果。