基于统计的异常检测方法S-H-ESD[twitter]
共 3763字，需浏览 8分钟
·
2020-11-27 19:16
↑↑↑点击上方蓝字，回复资料，10个G的惊喜
by：RandomWalk 阿里巴巴 算法工程师
Automatic Anomaly Detection in the Cloud Via Statistical Learning[1]
原文主要介绍了twitter云系统中利用统计学习实现异常检测的自动化，下面直接介绍相关方法。
Grubbs Test
表示一组时间序列，Grubbs test 检测单变量数据集的“最异常点“。前提假设数据分布是正态的。Grubbs test假设定义如下：
：数据集中没有异常点
: 数据集中有至少一个异常点
Grubbs‘ test 统计量定义如下
其中 
和 
分别表示数据集的均值和方差。对于双边检验，当满足式(2)时，以显著性水平 
拒绝原假设
其中 
表示自由度 
，显著性水平 
的 
分布的上临界值。对于单边检验，变为
[2]。但是缺点是数据集中存在多个异常点则不适合，因为 分布表不会更新。下面介绍多异常点的检测算法ESD（Extreme Studentized Deviate）[3]。
ESD
ESD可以检测时间序列数据的多异常点。需要指定异常点比例的upper bound是k，最差的情况是至多49.9%。实际中，数据集的异常比例一般不超过5%。ESD假设定义如下：
：数据集中没有异常点
: 数据集中有至多 
个异常点
检验统计量和临界值分别定义如下
其中 
，ESD会重复 次检验，当 
时，则有至少 个异常点。对于Grubbs Test和ESD的区别[4]，主要两点：一是ESD会根据不同的离群值调整临界值；二是ESD一直会检验 个离群点，而Grubbs test可能会提前结束检验（当“最异常点”检验时 成立）。比如下面Rosner paper中的数据，设置 
，第一次和第二次检验接受原假设，由于剔除前两个值之后临界值 
的变化，在第三次检验拒绝了原假设，因此最终得到三个异常点。
S-ESD
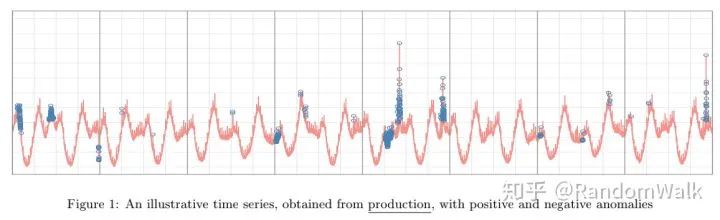
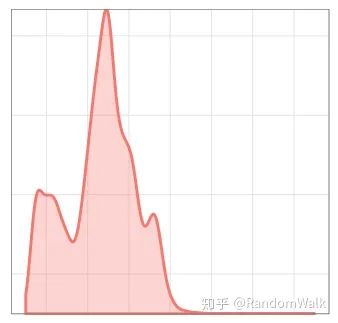
考虑ESD有如下两个限制：一是对于具有季节性的时间序列异常不能很好的识别，下图1中很多周期性变化的点并非异常点；二是多峰分布的数据点，一些低峰异常数据点不能被识别出来，如图2。
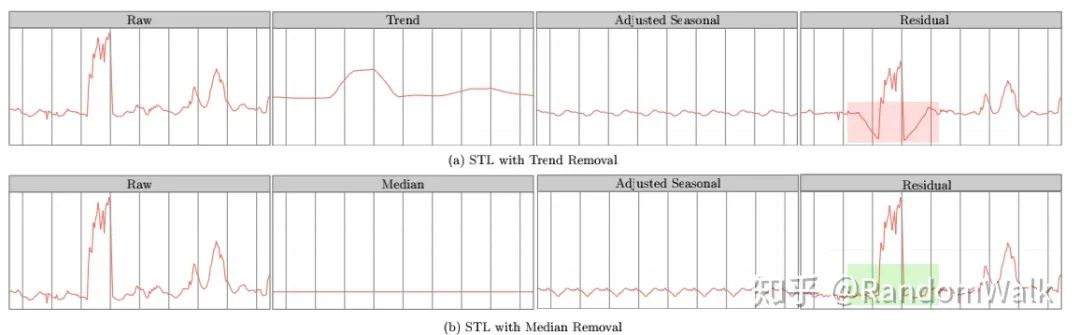
因此介绍S-ESD（Seasonal-ESD），Algorithm 1 中主要的不同是对时间序列数据进行STL分解，剔除其中的季节项，中位数做为趋势项（STL Variant），对残差项进行ESD检验。STL variant不同于STL主要考虑图3的情形，（a）中的STL分解得到的残差项，其中红色阴影部分存在spurious anomalies（这些点在原时间序列中并非异常）。
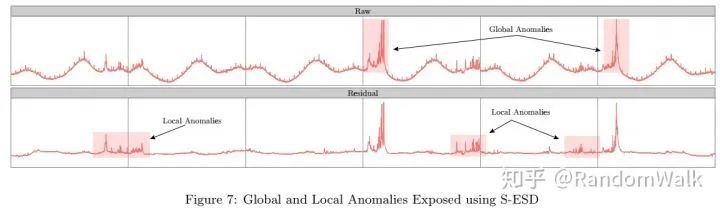
（局部异常和全局异常可识别性）S-ESD通过分解之后对残差项进行ESD检验，不仅可检验全局异常点，而且可以检验出如图4的局部异常点，这些异常点在原始数据中介于季节项的最大值和最小值之间，直接对原始数据ESD检验则无法识别。
S-H-ESD
但是S-ESD也有局限性，就是对于数据中含有异常点数量较多时，很难识别较多的异常点。因此下面介绍Seasonal Hybrid ESD (S-H-ESD)，首先介绍MAD。
MAD
考虑到ESD的检验统计量中的均值和方差对于过大的异常值较为敏感，于是选择利用MAD(Median Absolute Deviation)进行代替，如下
更一般的可以使用 
或者 
。
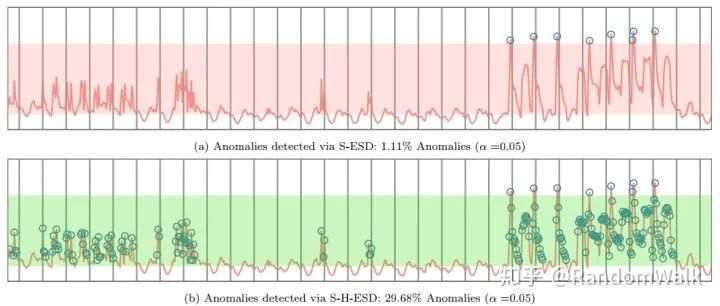
因此S-H-ESD相比S-ESD，是把ESD中的均值方差计算的统计量替换成MAD，图5比较了两种方法的效果，S-H-ESD对于异常点的识别率更高，同时由于计算中位数，时间复杂度也相对会更高。
python实现
推荐pyculiarity，原文的github地址是R的实现。
Pyculiarity是twitter时序数据异常检测AnomalyDetection[1]的python实现版本。主要是基于ESD（Extreme Studentized Deviate test）原理的异常检测算法。ESD的主要思想就是检验最大值、最小值偏离均值的程度是否为异常，具体可参考[2]。通过阅读pyculiarity的源码[3]，了解其主要包含两个方法：
detect_ts：用于时序数据，输入的DataFrame需要两列数据，其中一列为时间，另一列为该时间点对应的值
detect_vec：用于向量数据，可以不包含是时间列，时间索引按照DataFrame长度自动生成。
主要参数：
df：包含时间和值的DataFrame
max_anoms=0.10：发现异常数据的量（占总体的百分之多少）
direction=’pos’：’pos’是发现数据突增点，’neg’是发现数据突降点，’both’是包含突增与突降
alpha=0.05：接受或拒绝显著性水平，即p-value
only_last=None：仅再时间序列最后1天（’day’）或1小时（’hr’）寻找异常
threshold=None：仅报告高于指定阈值的正向异常。选项有：
med_max：每日最大值的中位数
p95：每日最大值的95%
p99：每日最大值的99%
e_value=False：返回数据中新增一列期望值
longterm=False：当时间序列超过一个月时，设置此值，
piecewise_median_period_weeks=2：当设置longterm后需要设置该值，设置滑动窗口的大小，注意这里需要>=2
plot=False：输出图像，已经不支持
y_log=False：对Y轴值取对数
xlabel = ”：添加输出到图形的X轴标签
ylabel = ‘count’：添加输出到图形的Y轴标签
title=None：输出图像的标签
verbose=False：是否输出debug信息
示例代码：
//data为包含[时间，数值]两列的dataframe
results=detect_ts(data,max_anoms=0.4,alpha=0.05,direction='both',only_last=None,longterm=True, piecewise_median_period_weeks=2)
//结果可视化
data['timestamp'] = pd.to_datetime(data['timestamp'])
data.set_index('timestamp', drop=True)
f, ax = plt.subplots(2, 1, sharex=True)
ax[0].plot(data['timestamp'], data['value'], 'b')
ax[0].plot(results['anoms'].index, results['anoms']['anoms'], 'ro')
ax[0].set_title('Detected Anomalies')
ax[1].set_xlabel('Time Stamp')
ax[0].set_ylabel('Count')
ax[1].plot(results['anoms'].index, results['anoms']['anoms'], 'b')
ax[1].set_ylabel('Anomaly Magnitude')
plt.show()参考
^Hochenbaum J, Vallis O S, Kejariwal A. Automatic anomaly detection in the cloud via statistical learning[J]. arXiv preprint arXiv:1704.07706, 2017.
^Francisco Augusto Alcaraz Garcia. Tests to identify outliers in data series. Pontifical Catholic University of Rio de Janeiro, Industrial Engineering Department, Rio de Janeiro, Brazil, 2012.
^Bernard Rosner. On the detection of many outliers. Technometrics, 17(2):221–227, 1975.
^https://www.itl.nist.gov/div898/handbook/eda/section3/eda35h3.htm
^https://github.com/twitter/AnomalyDetection
