数据特征预处理——数据降维
一、数据的降维方法
这里的意思不是说将多维数据降为低维数据,比如说,将三维降为二维这种,而是减少相关度低的特征数据。
1)特征选择
冗余: 部分特征的相关度高,容易消耗计算性能。噪声: 部分特征对预测结果有影响。
主要方法:Filter(过滤式):VarianceThreshol;Embeded(嵌入式):正则化,决策树;Wrapper(包裹式);神经网络==> 后续深入。 API:sklearn.feature_selection.VarianceThreshold(threshold=0.0)
删除所有低方差特征;Variance.fit_transform(X),X:numpy array 格式的数据;返回值: 训练集差异低于threshold的特征将会被删除;默认值是保留所有非零方差特征,即删除所有样本中具有相同值的特征。
from sklearn.feature_selection import VarianceThreshold
from sklearn.decomposition import PCA
import pandas as pd
def filter_Variance():
'''
删除低方差的数据
指定阈值方差
调用fit_transform
:return:
'''
var = VarianceThreshold(threshold=1.0)
data = var.fit_transform([[0,2,0,3],[0,1,4,3],[0,1,1,3]])
print(data)
'''
默认 threshold=0.0
[[2 0]
[1 4]
[1 1]]
取方差为1.0
[[0]
[4]
[1] ]
'''
return None
2)主成分分析
本质:PCA是一种分析、简化数据集的技术。
目的:是数据维数压缩,尽可能降低原数据的维数(复杂度),损失少量信息。
作用:可以削减回归分析或者聚类分析中特征的数量。特征数量达到上百的时候,考虑数据的简化(即PCA)。API:skelarn.decomposition。PCA(n_compoents = None):当n_compoents为小数时,降维到百分比(0-1之间,90%-95%最好);整数时降到相应个数,将数据分解为较低维度空间PCA.fit_transform(X);返回值:转换后指定维度的array。
def pca():
'''
主成分分析,数据特征降维
指定减少后的维度
调用fit_transform
:return:
'''
pca = PCA(n_components = 0.9)
data = pca.fit_transform([[2,8,4,5],[6,3,0,8],[5,4,9,1]])
print(data)
'''
[[ 1.28620952e-15 3.82970843e+00]
[ 5.74456265e+00 -1.91485422e+00]
[-5.74456265e+00 -1.91485422e+00]]
'''
return None
二、数据降维实例
InstaInstacart市场篮子分析cart市场篮子分析
products 商品信息:product_id,aisle_id,department_id
order_products__prior 订单与商品的信息:order_id,product_id,
orders 用户的订单信息: order_id,user_id,
aisles 商品所属具体物品类别:aisle_id
products ,order_products_prior,以及两表合并的数据如图:
def groupByUser():
'''
products 商品信息 product_id,aisle_id,department_id
order_products__prior 订单与商品的信息 order_id,product_id,
orders 用户的订单信息: order_id,user_id,
aisles 商品所属具体物品类别 aisle_id
数据降维,将用户分类
:return:
'''
#数据处理:先读取四张表
products = pd.read_csv(r"./files/products.csv")
prior = pd.read_csv(r'./files/order_products__prior.csv')
oriders = pd.read_csv(r'./files/orders.csv')
aisles = pd.read_csv(r"./files/aisles.csv")
#将四张表数据合并为一张表
# print(products.head())
# print(prior.head())
df1 = pd.merge(products,prior,left_on="product_id",right_on="product_id")
# print(df1.head())
df2 = pd.merge(df1,oriders,on=["order_id","order_id"])
df3 = pd.merge(df2,aisles,on=["aisle_id","aisle_id"])
print(df3.head())
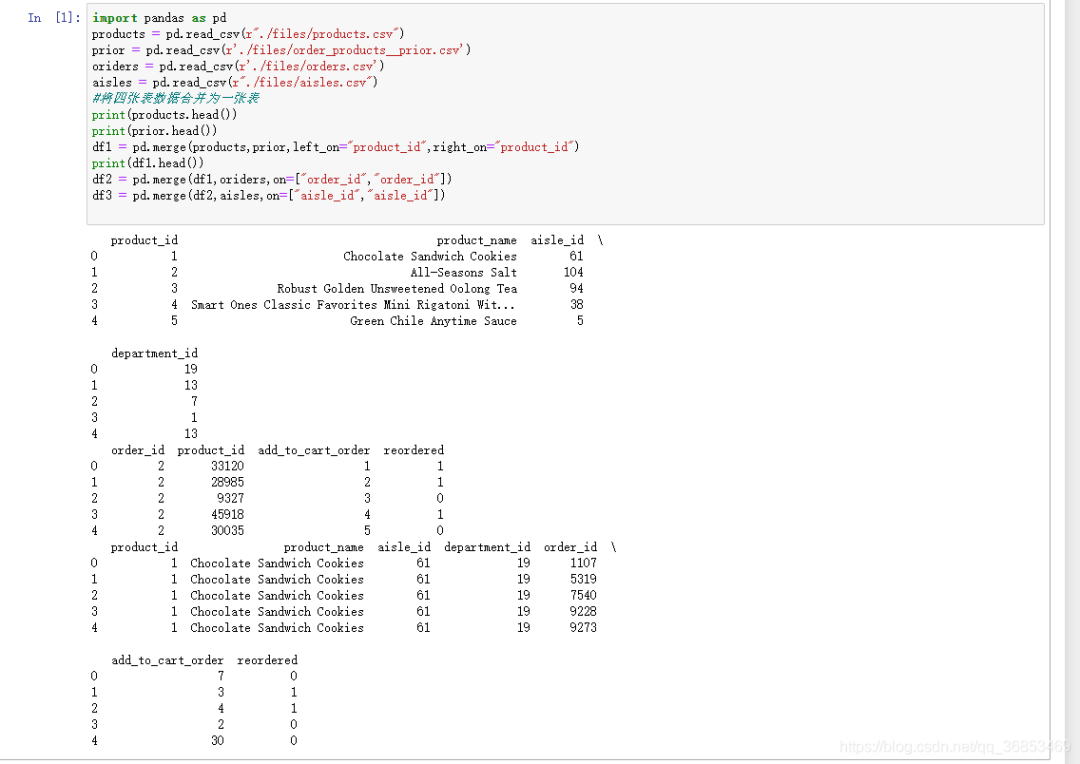
数据交叉
#交叉表:特殊的分组工具
cross = pd.crosstab(df3.user_id,df3.aisle)
print(cross.head()) #每个人买了多少个某个商品 10行 134个样本特征
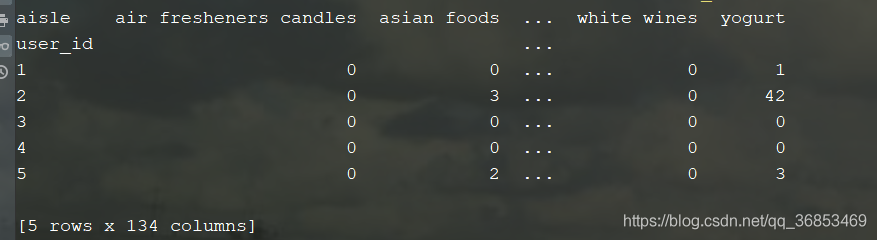
进行主成分分析
pca = PCA(n_components=0.9)
data = pca.fit_transform(cross)
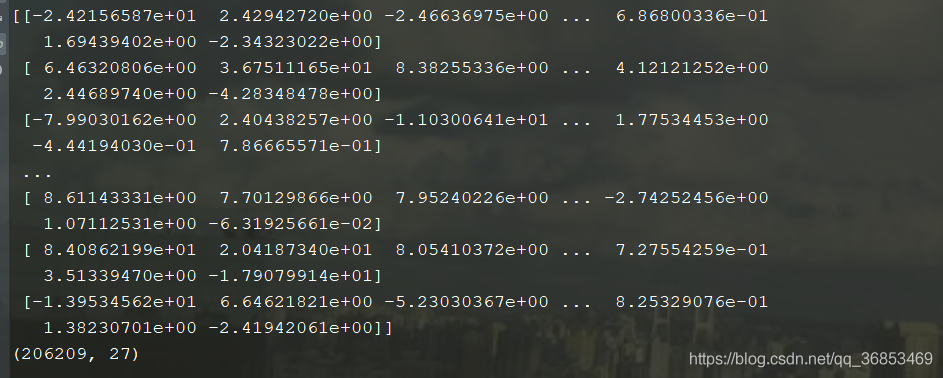
print(data)
print(data.shape) #27个特征
《数据科学与人工智能》公众号推荐朋友们学习和使用Python语言,需要加入Python语言群的,请扫码加我个人微信,备注【姓名-Python群】,我诚邀你入群,大家学习和分享。
关于Python语言,有任何问题或者想法,请留言或者加群讨论。
评论
