八十九、动态规划系列背包问题之完全背包
「@Author:Runsen」
动态规划需要搞定三个系列:三个背包,零钱问题和股票问题。今天就开始干掉三个背包问题。
三个背包问题:01背包,多重背包,完全背包。上次搞定了01背包,那么继续学习完全背包。
我们有种物品,物品的重量为,价格为。我们假定所有物品的重量和价格都是非负的,背包所能承受的最大重量W,每种物品都有无限件可用,则该问题成为完全背包问题 。
题目来源:https://www.acwing.com/problem/content/description/3/
先上代码,和01背包问题的解法有略微的改动,区别在于「遍历体积时从逆序改为顺序」,就只有这一个不同,在上一篇博客中有关于01背包问题的理解。
# 代码基本一样
n, v = map(int, input().split())
goods = []
for i in range(n):
goods.append([int(i) for i in input().split()])
dp = [0 for i in range(v+1)]
for i in range(n):
for j in range(v+1): # 从前往后
if j >= goods[i][0]:
dp[j] = max(dp[j], dp[j-goods[i][0]]+goods[i][1])
print(dp[-1])
# 测试代码
5 10
1 2
2 3
3 4
4 5
5 6
20
下面是有关完全背包的题目
Leetcode 279. 完全平方数
给定正整数 n,找到若干个完全平方数(比如 1, 4, 9, 16, ...)使得它们的和等于 n。你需要让组成和的完全平方数的个数最少。
示例 1:
输入: n = 12
输出: 3
解释: 12 = 4 + 4 + 4.
示例 2:
输入: n = 13
输出: 2
解释: 13 = 4 + 9
首先,明确dp,然后找dp的转移方程。
这里,dp[i]:表示完全平方数和为i的 最小个数。这个是没有任何问题的,关键是dp的转移方程。
对于Runsen这个菜鸟来说,也很快指的这是转移方程,就是i减去k 加上1。本质上就是斐波那契数列的一个变形。
「问题就转为了求n的最大平方和的序列。」
i = 1
nums = []
while i*i <= n:
nums.append(i*i)
i = i + 1
然后就是完全背包的反例的问题了。那么这个动态规划的问题基本解决了。
n = int(input())
i = 1
nums = []
while i*i <= n:
nums.append(i*i)
i = i + 1
print(nums)
# dp = [0] * (n+1) 是求最大值,[float('inf')] * (n+1)求最小值
# 如果写成 dp = [0] * (n+1) ,那么永远0最小
dp = [float('inf')] * (n+1)
dp[0] = 0
for i in range(1,n+1):
# j 是平方数
for j in nums:
if i<j:
break
dp[i] = min(dp[i], dp[i - j] + 1)
print(dp[-1])
下面代码来源官方的动态规划,和Runsen的基本一样。
import math
def numSquares(n):
"""
:type n: int
:rtype: int
"""
square_nums = [i ** 2 for i in range(0, int(math.sqrt(n)) + 1)]
dp = [float('inf')] * (n + 1)
# bottom case
dp[0] = 0
for i in range(1, n + 1):
for square in square_nums:
if i < square:
break
dp[i] = min(dp[i], dp[i - square] + 1)
return dp[-1]
顺便补充一下:「四平方定理」:任何一个正整数都可以表示成不超过四个整数的平方之和。推论:满足四数平方和定理的数n(四个整数的情况),必定满足
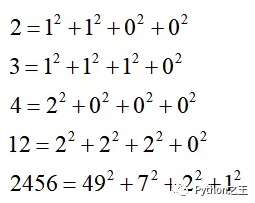
这个自己是不知道的,大家想深入:https://leetcode-cn.com/problems/perfect-squares/solution/wan-quan-ping-fang-shu-by-leetcode/
下面是四平方定理的代码
def numSquares(self, n):
"""
:type n: int
:rtype: int
"""
while n % 4 == 0:
n /= 4
if n % 8 == 7:
return 4
a = 0
while a**2 <= n:
b = int((n - a**2)**0.5)
if a**2 + b**2 == n:
return (not not a) + (not not b)
a += 1
return 3
Leetcode 300 最长上升子序列
给定一个无序的整数数组,找到其中最长上升子序列的长度。
示例:
输入: [10,9,2,5,3,7,101,18] 输出: 4 解释: 最长的上升子序列是 [2,3,7,101],它的长度是 4。说明:
可能会有多种最长上升子序列的组合,你只需要输出对应的长度即可。你算法的时间复杂度应该为 O(n2) 。
对于Runsen这个菜鸟来说,关键还是怎么找出dp和转移方程,dp[i]是第i个最长上升子序列。那么
class Solution:
def lengthOfLIS(self, nums: List[int]) -> int:
# 如果定义dp dp[i] 最长上升子序列 那么 dp[i] = max(dp[i], dp[k] + 1) 0<k<i-1
m = len(nums)
if m <= 1:
return m
dp = [ 1 for _ in range(m)]
for i in range(1,m):
for j in range(i):
if nums[i] > nums[j]:
dp[i] = max(dp[i], dp[j]+ 1 )
return max(dp)
Leetcode 322 零钱兑换
给定不同面额的硬币 coins 和一个总金额 amount。编写一个函数来计算可以凑成总金额所需的最少的硬币个数。如果没有任何一种硬币组合能组成总金额,返回 -1。
示例 1:
输入: coins = [1, 2, 5], amount = 11 输出: 3 解释: 11 = 5 + 5 + 1 示例 2:
输入: coins = [2], amount = 3 输出: -1
「零钱兑换实际上就是完全背包的题目,也可以看作下楼梯的问题的变种」
class Solution:
def coinChange(self, coins: List[int], amount: int) -> int:
# 第一步:定义dp数组或变量,首先明确题目说每种硬币的数量是无限的,但是会给定一个固定的 amount 金额,我们需要用最少的硬币数凑出这个金额,如果是01背包问题就是[0]开始;
# 因此这个是一个完全背包的题目,还是下楼梯的问题的变种。完全背包求最小,那么初始就要时最大
dp = [float('inf')] * (amount + 1)
# 计算的起点 0 块钱当然是 0
dp[0] = 0
# 状态转移方程:f(11) = min(f(10),f(9),f(6)) + 1
for i in range(amount + 1):
for j in coins:
if i-j >=0 :
dp[i] = min(dp[i],dp[i-j] + 1 )
if dp[amount] > amount:
# 如果dp[amount] 是amount + 1 ,说明了没有匹配的方式
return -1
return dp[-1]
「至此完全背包就到这里结束了,完全背包注意dp的定义,求最大还是最小,完全背包的关键词就次数是无限的」
更多的文章
点击下面小程序
- END -

