线性代数一百问之二:伴随矩阵这么巧妙,怎么来的?
伴随矩阵(Adjoint matrix),这个名词是 Maxime Bôcher 在 1907 年出版的《Introduction to Higher Algebra》中首次引入的。
也就是说并不像是谁直接提出这个概念的,那它大概怎么来的呢?根据一些历史资料及本人大胆推测,大致是由行列式,到拉普拉斯展开式,再到伴随矩阵,这么个路径。但这期间可能还涉及高斯的工作,这部分内容放在本文后面部分。
1Laplace 展开式
行列式的英文单词是 determinant,是决定因素或者决定性的的意思。那它到底是要决定什么呢?
行列式最初定义为线性方程组的一个属性,它决定了该线性方程组是否具有唯一解,即如果行列式不等于零,则方程组有唯一解。如果行列式等于零,则方程组有无穷多组解或者无解。
后来随着矩阵概念的诞生,行列式能够用来表征矩阵以及由矩阵表示的线性映射的一些属性。特别地,当且仅当矩阵可逆且矩阵表示的线性映射是同构时,行列式是非零的。
不过本文主要看行列式的定义与计算。
+行列式的定义
对于
其中,总和取于
我们都知道,当矩阵阶数为
+n = 2 时
+n = 3 时
按第
此处可以插入一个图,更形象地展示上述展开过程。
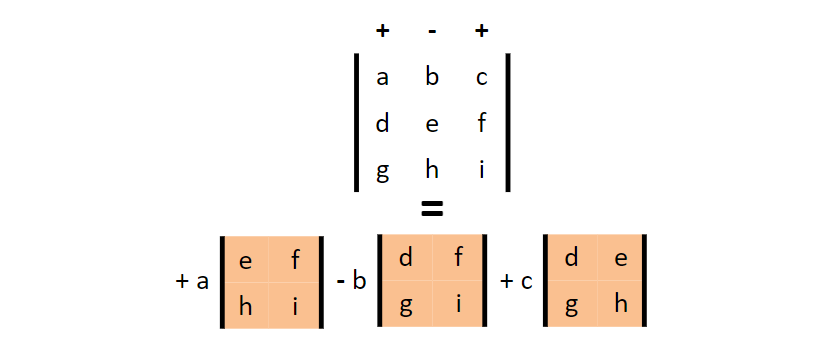
接下来就是开启找规律的模式,看看当矩阵的阶数升高后有没有类似的计算套路。
当矩阵的阶数增加上去会怎么样呢?答案是仍然有类似的结论,那就是 Laplace 展示式。
+Laplace 展开式
上面的试探可以发现,
其中
而
Laplace 展开式里的第一条是可以拿来递归式求解行列式(只是效率并不高)。值得注意的是第二条,它的意思就是只要按错误的行或列(
这两条要放在一起观察,从形式上看,像不像两个矩阵相乘的姿势?即
矩阵的对角化一直是数学家的追求,现在得到的不仅是对角化,甚至是单位(矩阵)化了,哪还有不欢喜的理由?
总之,我们得到了下面这个式子,
命题 令
其中,
我们来看一下当
这里为什么不直接除以
而当矩阵可逆时,这提供了一种逆矩阵的表示以及计算方案,估计是为了叫起来方便一些,于是给它一个名分。看它俩左右相伴,就叫做伴随矩阵呗。
值得注意的是,这里的伴随与伴随算子中的伴随没有关系,不用去强行将两者联系起来。
这个伴随矩阵听着名字挺香的,构思也挺巧妙的,只是用处大吗?
矩阵的一个重要用处是拿来表示线性变换,比如向量在矩阵的作用下可以变成另一个向量,那么有时候就要求能够变回来是吧。
因此,矩阵有必要和它的另一半成双成对出现,而伴随矩阵就是差不多充当这么个角色,它与逆矩阵也只差一个因子。
如果矩阵不可逆,即行列式为
此时伴随矩阵与齐次线性方程组
好了,接下来让我们想一想,伴随矩阵还有其他的用途吗?
2二次型的伴随式
我们直入主题,现有如下二次型,
由它可以衍生出另一个二次型,
这是变元
仔细看上面这个行列式,它将行列式、二次型以及伴随矩阵等融合在一起,十分巧妙。
这个事情似乎跟高斯的工作有关,高斯在研究如下表示的三元二次型时,
引入了它的伴随式子,
其中,
高斯在他的《算术探究》里引入上述概念,但那会儿还没矩阵,转化为矩阵的形式就对应如下两个矩阵。
和
这应该是二次型伴随式的原型,也可能是伴随矩阵这个名词的来源之一。
3附录
+命题的证明
可以从元素级别暴力证明。首先如下定义一个矩阵
左右两边矩阵的相应元素相等,得
当
以及,
比较两边元素,得
这是按列展开,跟上面类似,得
因此,如果
