红黑树的理解与 Java 实现
前言 红黑树的性质 红黑树的操作 1. 查找操作 2. 插入操作 3. 删除操作 Java实现 总结
前言
前段时间在研究 JDK1.8 的 hashmap 源码,看到 put 方法的插入环节,遇到了红黑树,不得不停止阅读源码的过程,因为还没掌握红黑树是无法完全读透 hashmap 源码的。红黑树作为一种数据结构,它被应用得非常多,可能很多人不认识它,但其实它已经在默默为我们的代码在发光发热。例如,你只要在 Java 中用到 map,基本上就是在用红黑树(当元素个数到达八个时链表转红黑树)。
PS:在看这篇文章前,必须先了解普通的二叉查找树和平衡查找树(AVL)树、2-3-4树。不然看起来会非常吃力。
红黑树的性质
红黑树是一种自平衡树,它也是一颗二叉树。既然能保持平衡,说明它和 AVL 树类似,在插入或者删除时肯定有调整的过程,只不过这个调整过程并不像 AVL 树那样繁琐。为何红黑树使用得比 AVL 树更多,就是因为红黑树它的调整过程迅速且简介。红黑树有以下五个特性:
性质1:节点是红色或黑色 性质2:根是黑色 性质3:所有叶子都是黑色。叶子是 NIL 节点,也就是 Null 节点 性质4:如果一个节点是红的,则它的两个儿子都是黑的 性质5:从任一节点到其叶子的所有简单路径都包含相同数目的黑色节点。
下图展示了一棵红黑树。
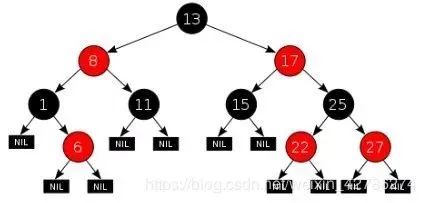
分析:
注意理解上,叶子并不等价于黑色节点,但是他们的颜色都是黑色。
为何要给节点指定红或者黑的颜色?
作者这种设计,只是为了从编程上达到一种便利的效果。另外可以让它们在插入时达到近似的平衡,并不像 AVL 树那样绝对平衡。实际上,红黑树是2-3树的一种变体,某种情况下,它又相当于2-3-4树。因为2-3树在编程上需要比较多的代码量,所以诞生了红黑树这种巧妙的设计。通过加了颜色来区分结点,这样编程上就可以当成二叉树来写程序,不用分别用三个指针表示左、中、右孩子了。
看一下红黑树和2-3树的等价性联系
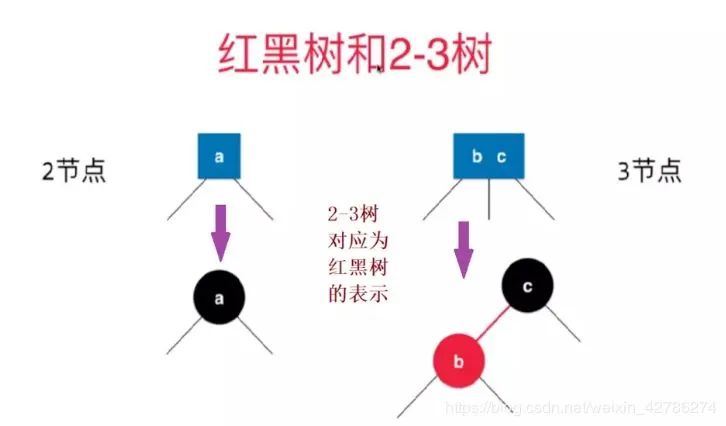
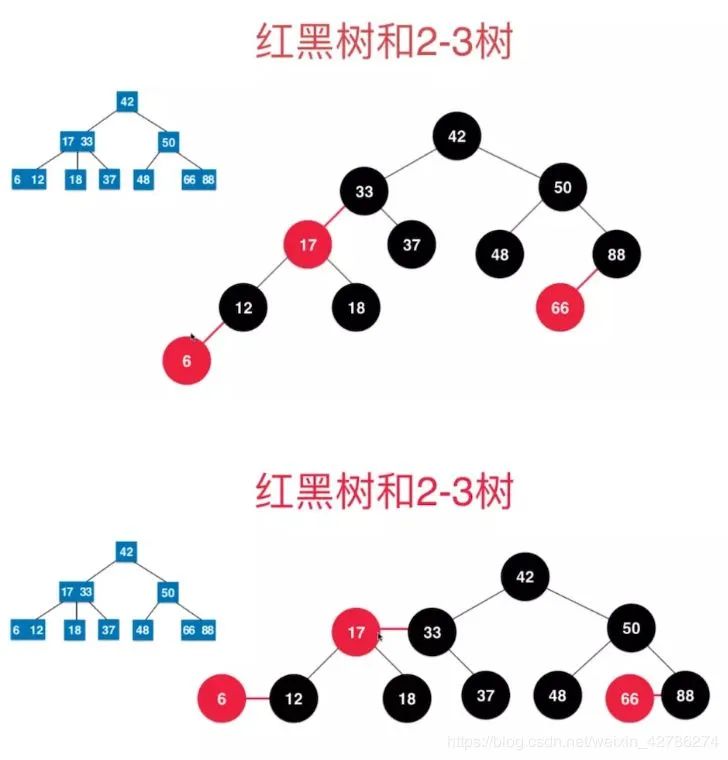
从上面可以看到,把红色节点放到与父亲齐平,就是2-3树中的一个2-3节点。
红黑树的操作
数据结构的性质看完之后,就要掌握它到底会存在哪种操作?例如 hashmap,它最常见的操作就是 get 和 put、扩容。同理,红黑树也有它的基本操作。因为它本身上也是一棵二叉查找树,所以重点关注的操作无非就是查找、插入、删除。
1. 查找操作
红黑树的查找方式很简单,只要是树,查找的过程无非就是一个递归过程。如果查找的元素小于当前节点,那么查找其左子树;如果查找的元素大于当前元素,则查找其右子树。
2. 插入操作
插入操作首先需要通过查找操作找到合适的插入点,然后插入新节点。如果在插入节点后,发生了违背红黑树特性的情况时,需要对红黑树进行旋转染色等操作,使其重新满足特性。
2.1 插入新节点
为了在插入新节点时尽可能少的违反红黑树特性且更容易调整红黑树,就先将新节点染成红色。这样就只可能会违反特性4。如果这里没有违反特性4,那么就不需要对红黑树进行调整,插入操作完成。
2.2 调整子树
那么,在违反了特性4的时候,新节点的父节点为红色节点。根据特性2可知,父节点不是根节点,则新节点必有祖父节点。又根据特性3可推论出红色节点必有两个黑色子节点(空节点为黑色)。此时会出现两种情况:叔节点为红色、叔节点为黑色。
图例:C 表示当前节点,P 表示父节点,U 表示叔节点,G 表示祖父节点
(1)父节点与叔节点都为红色的情况
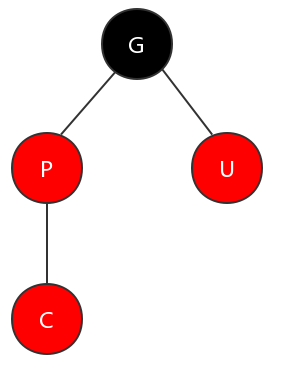
在这种情况下,需要将父节点和叔节点变为黑色,再将祖父节点变为红色。这样,图上所展示的子树就满足了红黑树的特性。如下图所示。
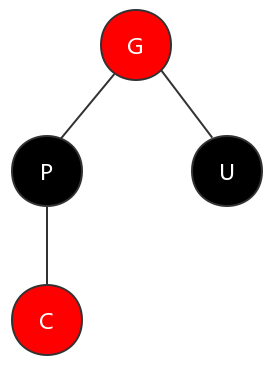
但是这里又可能会产生新的违反特性情况,因为祖父节点变成了红色,那么它可能会造成违反特性4的情况。所以,这里就将祖父节点作为当前节点,进行新一轮的调整操作。
(2)父节点为红色,叔节点为黑色的情况
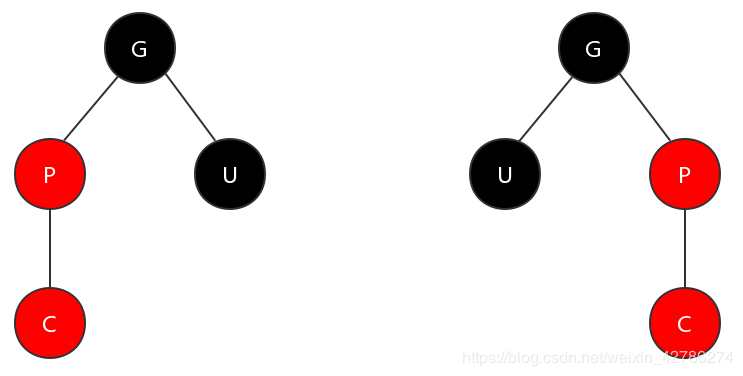
在这种情况下,对其调整的核心就是保持父节点分支符合特性4,而叔节点分支保持符合特性5。
第一步,旋转。对祖父节点进行左旋或者右旋。如果父节点是祖父节点的右子节点,那么对祖父节点进行左旋;否则,对祖父节点进行右旋。 第二步,染色。将祖父节点染为红色,而父节点染为黑色。
进过这两步,上图的情况会转换为下图所示。
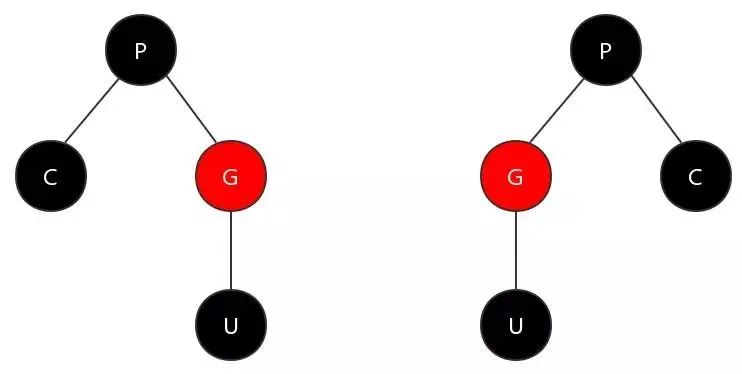
可以看出,父节点这一分支进过调整后,当前节点与父节点的颜色不再是连续红色,满足特性4。而叔节点这一分支的黑色节点数目没有发生变化,满足特性5。对原祖父节点的父节点来说,该子树没有发生违反特性的变化。该子树调整完成。
2.3 检查根节点
当上述调整执行完后,还有最后一步,就是检查是否满足特性2。这一步只需要将根节点染成黑色就可以,无需再多加判断。
3. 删除操作
需要重点理解的就是删除操作,这个也是我觉得是红黑树中最难的部分。
删除操作要比插入操作略微复杂一些。因为删除的节点可能是出现在树的中间层的节点,此时删除该节点会遇到很复杂的情况。所以,在删除节点的时候,需要先对红黑树进行一些调整,使得删除节点对整个树的影响降到最低。
3.1 替换删除节点
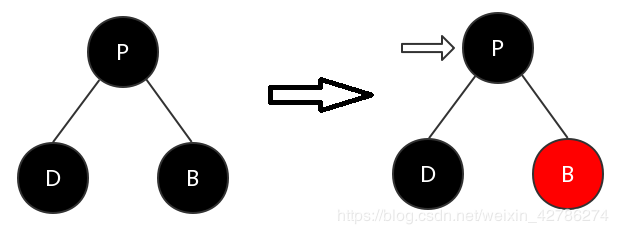
首先根据 BST 删除节点的规则,使用当前节点左子树的最大值节点或者右子树的最小值节点代替其删除。这两个节点是其子树中数值上最贴近当前节点数值的节点)。这一点,只要懂了二叉查找树的删除操作就明白了,在这里不多说了。如下图所示:
图例:D 表示当前节点,P 表示父节点,B 表示兄弟节点,BR 表示兄弟节点的右子节点,BL 表示兄弟节点的左子节点
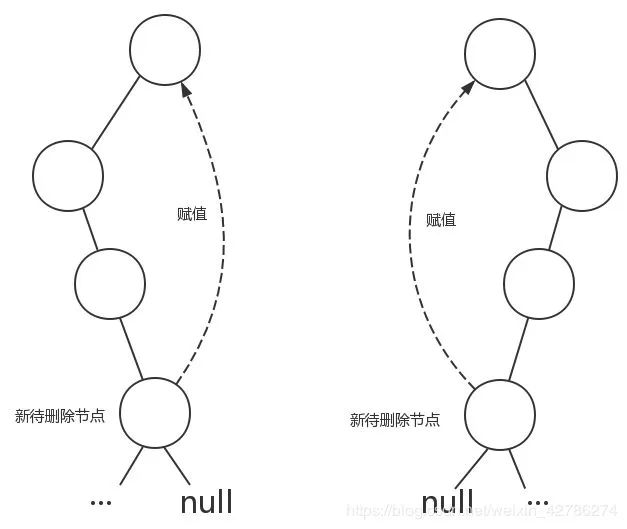
既然待删除节点是要被移走的,那肯定有一个节点要替换到它的位置上去。如何找到这个替换节点,这个过程和二叉查找树一模一样,要么在它的左子树下一直往右找到最大节点,要么在右子树下找到最小节点。
下面的描述过程采用的是右子树的最小值节点代替
当找到替换节点之后,现在需要考虑的情况就减少了,只可能会出现以下几种情况(因为需要满足红黑树特性):
无子节点,节点为红色 无子节点,节点为黑色 只有右子节点,右子节点为红色,节点本身为黑色
上面这三种情况,说的是新待删除节点。新待删除节点,就是即将被替换到待删除位置的节点。
因为 D 节点就是即将要替换到待删节点位置的节点,它同时又是右子树的最小值,既然是最小值了,它就不再可能拥有左子树了,所以只有可能有右子节点。另外,假如它有右节点且右节点的颜色是黑色,它自身颜色是红色,根本不成立。因为假如它自身为红色且又有黑孩子,那它必须要有两个黑孩子才满足红黑树性质,所以不满足。那有没有可能,它自身是黑色且右孩子也为黑色呢?也不可能!因为它左孩子已经为空了,说明它从自身出发到左子树的叶子的距离就是1,假如它右孩子也为黑色,那它从自身出发到右子树叶子的距离肯定大于等于2了,明显不可能。
所以总的来说只可能有下面三种情况:
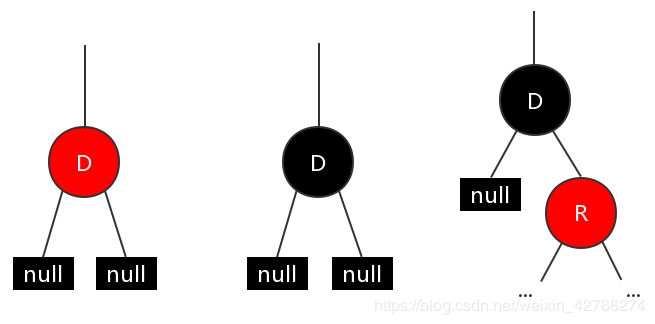
情况1:只需要直接删除节点就可以。删了一个红色新待删节点,不会影响红黑树性质。 情况2:删除该 D 节点后,违反了红黑树特性5,需要调整(不考虑待删除节点为根节点的情况) 情况3:用右子节点 R 占据待删除节点 D,再将其染成黑色即可,不违反红黑树特性。因为左边本来就是空了,其实右子树下即使有多少个黑色节点,也不会影响整体特性。
在这三种情况中,情况1和情况3比较简单,不需要多余的调整。情况2则需要后续的调整步骤使其满足红黑树特性。
3.2 调整红黑树
上述情况2的调整比较复杂。下面对各种情况进行讲解。
根据红黑树的特性5,待删除节点必然有兄弟节点。
为什么这么说呢?因为我们已经假设上面的 D 节点不为根了,那说明它肯定有父亲。首先它是没有孩子的,它下面直接就是叶子了,既然有父亲,不论它是父亲的左孩子或者右孩子,从父亲出发到它自身,黑色节点的个数为1。反证法:假如父亲只有它一个孩子,那说明父亲到另一边子树的叶子距离就为0,因为0个节点。这明显不符合,所以说明父亲肯定有两个孩子,那从而得知待删节点D必有兄弟。
下面根据其兄弟节点所在分支的不同,来分情况讨论。
以下是以关注待删节点为父节点的左子节点进行描述,如果遇到关注节点为父节点的右子节点的情况,则镜像处理。
**思路:**下面的任何调整只有一个目的,就是不断调整,直到调整到可以直接将 D 移除又不会影响红黑树特性的情况。但关键是调整过程中红黑树特性也不会发生改变。
图例:D 表示当前节点,P 表示父节点,B 表示兄弟节点,BR 表示兄弟节点的右子节点,BL 表示兄弟节点的左子节点
(1)兄弟节点为红色

将父节点染成红色,兄弟节点染成黑色,然后对父节点进行左旋操作。此时就转换为了下面的(4),之后按照(4)继续进行调整。
分析:这种情况,树的整体高度为2,变色左旋之后,整体高度还是保持在2。
(2)兄弟节点为黑色,远侄节点为红色
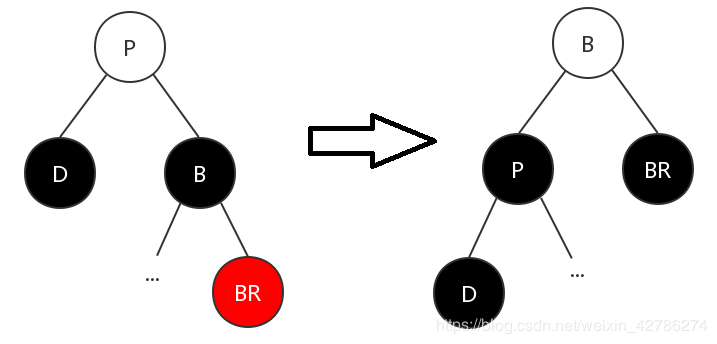
这种情况下,不需要考虑父节点的颜色。
将父节点 P 与兄弟节点 B 的颜色互换 ,这个过程父亲染黑 将兄弟节点的右子节点 BR 染成黑色 对父节点 P 进行左旋操作
可以看到,原本高度就是符合红黑树特性的,左右子树的高度都为1,因为黑色节点只有一个。经过这三步的调整后,直接删除节点 D 后仍然满足红黑树的特性,调整完成,跳出算法循环。
(3)兄弟节点为黑色,远侄节点为黑色,近侄节点为红色
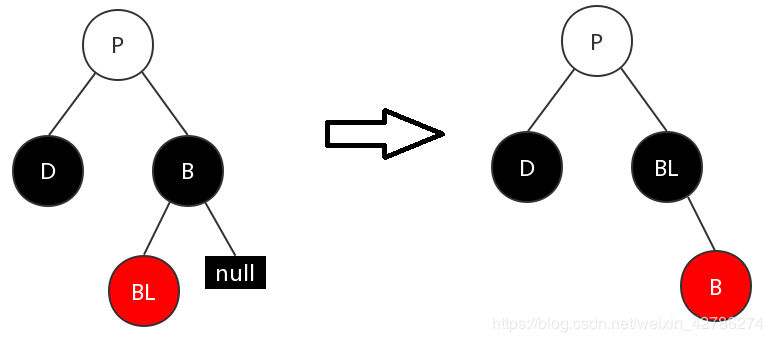
这种情况下,兄弟节点的左节点染成黑色。兄弟节点染红。然后对兄弟节点做右旋。此时的状况就和(2)一样了。之后就通过(2)的调整方式进行调整。
(4)父节点为红色,兄弟节点为黑色,兄弟节点无子节点
这种情况下,将父节点P染成黑色,再将兄弟节点染成红色。经过这样的操作后,除去节点D后,以P为根节点的子树的黑节点深度并没有发生变化。调整完成。
怎么理解这个操作?
可以看左边,没调整前,P 的左右子树的黑色结点的数目都是1,是相同的,符合红黑树的性质:从任一节点到其叶子的所有简单路径都包含相同数目的黑色节点。然后再看右边,调整后,删掉 D 之后,P 结点的左右子树的黑色结点都是0个,仍然满足性质,所以调整完成。
(5)父节点为黑色,兄弟节点为黑色,兄弟节点无子节点

这种情况下,为了在删除节点 D 后使以 P 为根节点的子树能满足红黑树特性5,将兄弟节点 B 染成红色。但是这样操作后,以 P 为根节点的子树的黑色节点深度变小了。所以需要继续调整。
因为P节点子树的黑色深度发生了减少,可以把其当作待删除节点,那么此时就以 P 节点为关注节点进行进一步调整(继续向上调整)。这句话的意思我们再以 P 为起始点,继续根据情况进行平衡操作。就是把 P 当成 D,只是不要再删除 P 了。再看是这五种中的哪种情况,再进行对应的调整,这样一直向上,直到新的起始点为根节点或者关注节点不为黑色。
第五种情况,不会一直连续回溯的。假如能一直回溯,指针向上走之后,兄弟节点会一直都没有右孩子吗?不存在的。假如有这种情况,说明树的路径长度已经严重往左倾斜,肯定不可能。所以回溯这个情况只会回溯一次,不会连续回溯。第五个这种情况出现之后,下一次进入算法循环,肯定就是进入其他情况,直到遇到 break,跳出循环,终止整个算法过程。
3.3 检查根节点及删除节点
经过上述的调整后,此时基本满足了红黑树的特性。但是存在根节点变成红色的情况。所以需要将根节点染成黑色的操作。最后,执行删除操作,将待删除节点删掉。
当然从编程的角度,你也可以调整指针先把待删除节点移掉,然后再开始平衡调整过程。注意这里说的平衡调整,并不是 AVL 树的绝对平衡调整,而是满足红黑树特性的平衡调整。红黑树的平衡和 AVL 的平衡是有区别的。
Java实现
上面的操作篇幅比较长,假如没看明白,可以通过下面的代码继续看。
由于篇幅限制,源码请到原文链接查看 Java 实现
blog.csdn.net/weixin_42786274/article/details/86557922
总结
红黑树的删除操作是整个红黑树中最复杂的一部分,理解了这部分,红黑树就算基本拿下了。理解完一种数据结构,要能 get 到作者当初设计时的点,才算是一次积累。红黑树的删除操作,它非常地巧妙,整一个算法循环过程,它不会超过三次,调整过程基本都在子树内完成,指针不需要一直向上回溯,相比 AVL 树,AVL 树在删除节点时,指针有可能会一直回溯到根为止。
来源:xyk_1021
blog.csdn.net/weixin_42786274/article/details/86557922
推荐阅读:
不是你需要中台,而是一名合格的架构师(附各大厂中台建设PPT)
