大家好，我是爱生活，AI风控的小伍哥，上次给大家带来第一篇文章OddBall，当时并未附代码，现在找到一个比较好的开源代码，分享给大家。

项目地址：https://github.com/gloooryyt/oddball_py3

我们自己构建测试数据或者读取测试数据

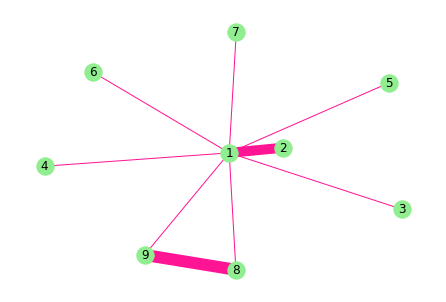
import networkx as nxG = nx.Graph(date="10.11",name="无向图")#创建空图，无向图G.add_node(1)G.add_nodes_from([1,2,3,4,5,6,7,8,9])G.nodes()G.add_weighted_edges_from([(1,2,10),(1,3,1),(1,4,1),(1,5,1),(1,6,1),(1,7,1),(1,8,1),(1,9,1),(8,9,1)])print(G.adj){1: {2: {'weight': 10}, 3: {'weight': 1}, 4: {'weight': 1}, 5: {'weight': 1}, 6: {'weight': 1}, 7: {'weight': 1}, 8: {'weight': 1}, 9: {'weight': 1}}, 2: {1: {'weight': 10}}, 3: {1: {'weight': 1}}, 4: {1: {'weight': 1}}, 5: {1: {'weight': 1}}, 6: {1: {'weight': 1}}, 7: {1: {'weight': 1}}, 8: {1: {'weight': 1}, 9: {'weight': 1}}, 9: {1: {'weight': 1}, 8: {'weight': 1}}}
import matplotlib.pyplot as pltedgewidth = [10,1,1,1,1,1,1,1,12]nx.draw(G,with_labels=True,        pos=nx.spring_layout(G),        width=edgewidth,        node_color="lightgreen",        edge_color="DeepPink")plt.show()

也可以读取自己的数据集

#数据读取import ospath = '/Users/wuzhengxiang/Downloads/OddBall10_tbox 2/oddball-edges.txt'

下面👇🏻是正式的代码

import numpy as npimport networkx as nx#load data, a weighted undirected graphdef load_data(path):      data = np.loadtxt(path).astype('int32')      G = nx.Graph()      for ite in data:          G.add_edge(ite[0], ite[1], weight=ite[2])      return Gdef get_feature(G):      #feature dictionary which format is {node i's id:Ni, Ei, Wi, λw,i}      featureDict = {}      nodelist = list(G.nodes)      for ite in nodelist:          featureDict[ite] = []          #the number of node i's neighbor          Ni = G.degree(ite)          featureDict[ite].append(Ni)          #the set of node i's neighbor          iNeighbor = list(G.neighbors(ite))          #the number of edges in egonet i          Ei = 0          #sum of weights in egonet i          Wi = 0          #the principal eigenvalue(the maximum eigenvalue with abs) of egonet i's weighted adjacency matrix          Lambda_w_i = 0          Ei += Ni          egonet = nx.Graph()          for nei in iNeighbor:              Wi += G[nei][ite]['weight']              egonet.add_edge(ite, nei, weight=G[nei][ite]['weight'])          iNeighborLen = len(iNeighbor)          for it1 in range(iNeighborLen):              for it2 in range(it1+1, iNeighborLen):                  #if it1 in it2's neighbor list                  if iNeighbor[it1] in list(G.neighbors(iNeighbor[it2])):                      Ei += 1                      Wi += G[iNeighbor[it1]][iNeighbor[it2]]['weight']                      egonet.add_edge(iNeighbor[it1], iNeighbor[it2], weight=G[iNeighbor[it1]][iNeighbor[it2]]['weight'])          egonet_adjacency_matrix = nx.adjacency_matrix(egonet).todense()          eigenvalue, eigenvector = np.linalg.eig(egonet_adjacency_matrix)          eigenvalue.sort()          Lambda_w_i = max(abs(eigenvalue[0]), abs(eigenvalue[-1]))          featureDict[ite].append(Ei)          featureDict[ite].append(Wi)          featureDict[ite].append(Lambda_w_i)      return featureDict

import numpy as npfrom sklearn.linear_model import LinearRegressionfrom sklearn.neighbors import LocalOutlierFactor  # feature dictionary which format is {node i's id:Ni, Ei, Wi, λw,i}def star_or_clique(featureDict):    N = []    E = []    for key in featureDict.keys():        N.append(featureDict[key][0])        E.append(featureDict[key][1])    #E=CN^α => log on both sides => logE=logC+αlogN    #regard as y=b+wx to do linear regression    #here the base of log is 2    y_train = np.log2(E)    y_train = np.array(y_train)    y_train = y_train.reshape(len(E), 1)    x_train = np.log2(N)    x_train = np.array(x_train)    x_train = x_train.reshape(len(N), 1)    model = LinearRegression()    model.fit(x_train, y_train)    w = model.coef_[0][0]    b = model.intercept_[0]    C = 2**b    alpha = w    outlineScoreDict = {}    for key in featureDict.keys():        yi = featureDict[key][1]        xi = featureDict[key][0]        outlineScore = (max(yi, C*(xi**alpha))/min(yi, C*(xi**alpha)))*np.log(abs(yi-C*(xi**alpha))+1)        outlineScoreDict[key] = outlineScore    return outlineScoreDict

def heavy_vicinity(featureDict):    W = []    E = []    for key in featureDict.keys():        W.append(featureDict[key][2])        E.append(featureDict[key][1])    #W=CE^β => log on both sides => logW=logC+βlogE    #regard as y=b+wx to do linear regression    #here the base of log is 2    y_train = np.log2(W)    y_train = np.array(y_train)    y_train = y_train.reshape(len(W), 1)    x_train = np.log2(E)    x_train = np.array(x_train)    x_train = x_train.reshape(len(E), 1)    model = LinearRegression()    model.fit(x_train, y_train)    w = model.coef_[0][0]    b = model.intercept_[0]    C = 2**b    beta = w    outlineScoreDict = {}    for key in featureDict.keys():        yi = featureDict[key][2]        xi = featureDict[key][1]        outlineScore = (max(yi, C*(xi**beta))/min(yi, C*(xi**beta)))*np.log(abs(yi-C*(xi**beta))+1)        outlineScoreDict[key] = outlineScore    return outlineScoreDict

def dominant_edge(featureDict):    Lambda_w_i = []    W = []    for key in featureDict.keys():        Lambda_w_i.append(featureDict[key][3])        W.append(featureDict[key][2])    #λ=CW^γ => log on both sides => logλ=logC+γlogW    #regard as y=b+wx to do linear regression    #here the base of log is 2    y_train = np.log2(Lambda_w_i)    y_train = np.array(y_train)    y_train = y_train.reshape(len(Lambda_w_i), 1)    x_train = np.log2(W)    x_train = np.array(x_train)    x_train = x_train.reshape(len(W), 1)    model = LinearRegression()    model.fit(x_train, y_train)    w = model.coef_[0][0]    b = model.intercept_[0]    C = 2 ** b    beta = w    outlineScoreDict = {}    for key in featureDict.keys():        yi = featureDict[key][3]        xi = featureDict[key][2]        outlineScore = (max(yi, C * (xi ** beta)) / min(yi, C * (xi ** beta))) * np.log(abs(yi - C * (xi ** beta)) + 1)        outlineScoreDict[key] = outlineScore    return outlineScoreDict

def star_or_clique_withLOF(featureDict):    N = []    E = []    for key in featureDict.keys():        N.append(featureDict[key][0])        E.append(featureDict[key][1])    #E=CN^α => log on both sides => logE=logC+αlogN    #regard as y=b+wx to do linear regression    #here the base of log is 2    y_train = np.log2(E)    y_train = np.array(y_train)    y_train = y_train.reshape(len(E), 1)    x_train = np.log2(N)    x_train = np.array(x_train)    x_train = x_train.reshape(len(N), 1)    #the order in x_train and y_train is the same as which in featureDict.keys() now
    #prepare data for LOF    xAndyForLOF = []    for index in range(len(N)):        tempArray = np.array([x_train[index][0], y_train[index][0]])        xAndyForLOF.append(tempArray)    xAndyForLOF = np.array(xAndyForLOF)
    model = LinearRegression()    model.fit(x_train, y_train)    w = model.coef_[0][0]    b = model.intercept_[0]    C = 2**b    alpha = w    print('alpha={}'.format(alpha))
    #LOF algorithm    clf = LocalOutlierFactor(n_neighbors=20)    clf.fit(xAndyForLOF)    LOFScoreArray = -clf.negative_outlier_factor_
    outScoreDict = {}    count = 0   #Used to take LOFScore in sequence from LOFScoreArray
    #get the maximum outLine    maxOutLine = 0    for key in featureDict.keys():        yi = featureDict[key][1]        xi = featureDict[key][0]        outlineScore = (max(yi, C*(xi**alpha))/min(yi, C*(xi**alpha)))*np.log(abs(yi-C*(xi**alpha))+1)        if outlineScore > maxOutLine:            maxOutLine = outlineScore
    print('maxOutLine={}'.format(maxOutLine))
    #get the maximum LOFScore    maxLOFScore = 0    for ite in range(len(N)):        if LOFScoreArray[ite] > maxLOFScore:            maxLOFScore = LOFScoreArray[ite]
    print('maxLOFScore={}'.format(maxLOFScore))
    for key in featureDict.keys():        yi = featureDict[key][1]        xi = featureDict[key][0]        outlineScore = (max(yi, C*(xi**alpha))/min(yi, C*(xi**alpha)))*np.log(abs(yi-C*(xi**alpha))+1)        LOFScore = LOFScoreArray[count]        count += 1        outScore = outlineScore/maxOutLine + LOFScore/maxLOFScore        outScoreDict[key] = outScore    return outScoreDict

def heavy_vicinity_withLOF(featureDict):    W = []    E = []    for key in featureDict.keys():        W.append(featureDict[key][2])        E.append(featureDict[key][1])    #W=CE^β => log on both sides => logW=logC+βlogE    #regard as y=b+wx to do linear regression    #here the base of log is 2    y_train = np.log2(W)    y_train = np.array(y_train)    y_train = y_train.reshape(len(W), 1)    x_train = np.log2(E)    x_train = np.array(x_train)    x_train = x_train.reshape(len(E), 1)    #the order in x_train and y_train is the same as which in featureDict.keys() now
    #prepare data for LOF    xAndyForLOF = []    for index in range(len(W)):        tempArray = np.array([x_train[index][0], y_train[index][0]])        xAndyForLOF.append(tempArray)    xAndyForLOF = np.array(xAndyForLOF)
    model = LinearRegression()    model.fit(x_train, y_train)    w = model.coef_[0][0]    b = model.intercept_[0]    C = 2**b    beta = w    print('beta={}'.format(beta))
    #LOF algorithm    clf = LocalOutlierFactor(n_neighbors=20)    clf.fit(xAndyForLOF)    LOFScoreArray = -clf.negative_outlier_factor_
    outScoreDict = {}    count = 0   #Used to take LOFScore in sequence from LOFScoreArray
    #get the maximum outLine    maxOutLine = 0    for key in featureDict.keys():        yi = featureDict[key][2]        xi = featureDict[key][1]        outlineScore = (max(yi, C*(xi**beta))/min(yi, C*(xi**beta)))*np.log(abs(yi-C*(xi**beta))+1)        if outlineScore > maxOutLine:            maxOutLine = outlineScore
    print('maxOutLine={}'.format(maxOutLine))
    #get the maximum LOFScore    maxLOFScore = 0    for ite in range(len(W)):        if LOFScoreArray[ite] > maxLOFScore:            maxLOFScore = LOFScoreArray[ite]
    print('maxLOFScore={}'.format(maxLOFScore))
    for key in featureDict.keys():        yi = featureDict[key][2]        xi = featureDict[key][1]        outlineScore = (max(yi, C*(xi**beta))/min(yi, C*(xi**beta)))*np.log(abs(yi-C*(xi**beta))+1)        LOFScore = LOFScoreArray[count]        count += 1        outScore = outlineScore/maxOutLine + LOFScore/maxLOFScore        outScoreDict[key] = outScore    return outScoreDict
def dominant_edge_withLOF(featureDict):    Lambda_w_i = []    W = []    for key in featureDict.keys():        Lambda_w_i.append(featureDict[key][3])        W.append(featureDict[key][2])    #λ=CW^γ => log on both sides => logλ=logC+γlogW    #regard as y=b+wx to do linear regression    #here the base of log is 2    y_train = np.log2(Lambda_w_i)    y_train = np.array(y_train)    y_train = y_train.reshape(len(Lambda_w_i), 1)    x_train = np.log2(W)    x_train = np.array(x_train)    x_train = x_train.reshape(len(W), 1)    #the order in x_train and y_train is the same as which in featureDict.keys() now
    #prepare data for LOF    xAndyForLOF = []    for index in range(len(W)):        tempArray = np.array([x_train[index][0], y_train[index][0]])        xAndyForLOF.append(tempArray)    xAndyForLOF = np.array(xAndyForLOF)
    model = LinearRegression()    model.fit(x_train, y_train)    w = model.coef_[0][0]    b = model.intercept_[0]    C = 2**b    gamma = w    print('gamma={}'.format(gamma))
    #LOF algorithm    clf = LocalOutlierFactor(n_neighbors=20)    clf.fit(xAndyForLOF)    LOFScoreArray = -clf.negative_outlier_factor_
    outScoreDict = {}    count = 0   #Used to take LOFScore in sequence from LOFScoreArray
    #get the maximum outLine    maxOutLine = 0    for key in featureDict.keys():        yi = featureDict[key][3]        xi = featureDict[key][2]        outlineScore = (max(yi, C*(xi**gamma))/min(yi, C*(xi**gamma)))*np.log(abs(yi-C*(xi**gamma))+1)        if outlineScore > maxOutLine:            maxOutLine = outlineScore
    print('maxOutLine={}'.format(maxOutLine))
    #get the maximum LOFScore    maxLOFScore = 0    for ite in range(len(W)):        if LOFScoreArray[ite] > maxLOFScore:            maxLOFScore = LOFScoreArray[ite]
    print('maxLOFScore={}'.format(maxLOFScore))
    for key in featureDict.keys():        yi = featureDict[key][3]        xi = featureDict[key][2]        outlineScore = (max(yi, C*(xi**gamma))/min(yi, C*(xi**gamma)))*np.log(abs(yi-C*(xi**gamma))+1)        LOFScore = LOFScoreArray[count]        count += 1        outScore = outlineScore/maxOutLine + LOFScore/maxLOFScore        outScoreDict[key] = outScore    return outScoreDict

一、概   述

基于图的异常检测分为 孤立点检测 和 异常群簇检测，本文是孤立点检测中较经典的论文，通过研究Ego-net总结几种异常模型及提供度量方式：

文章调查了Ego-net中存在的异常模式，并给出了检测异常模式的依据基于上述模式，提出了OddBall，一种用于异常点检测的无监督方法，将OddBall应用于真实数据集，并验证了算法的有效性

论文名称：OddBall: Spotting Anomalies in Weighted Graphs

论文地址：http://www.cs.cmu.edu/~mmcgloho/pubs/pakdd10.pdf

代码地址：https://www.andrew.cmu.edu/user/lakoglu/pubs.html#code

二、Ego-net（中心节点）

以中心节点(ego)及其邻居组成的子图，一般用于研究个体性质以及局部社区发现，本文仅考虑一阶邻居，这是为了减少计算量并提和高可解释性。

三、Ego-net模式及度量方法

1 、CliqueStar（基于密度）

基于密度的方法可以识别出下面两种Ego-net的异常结构：

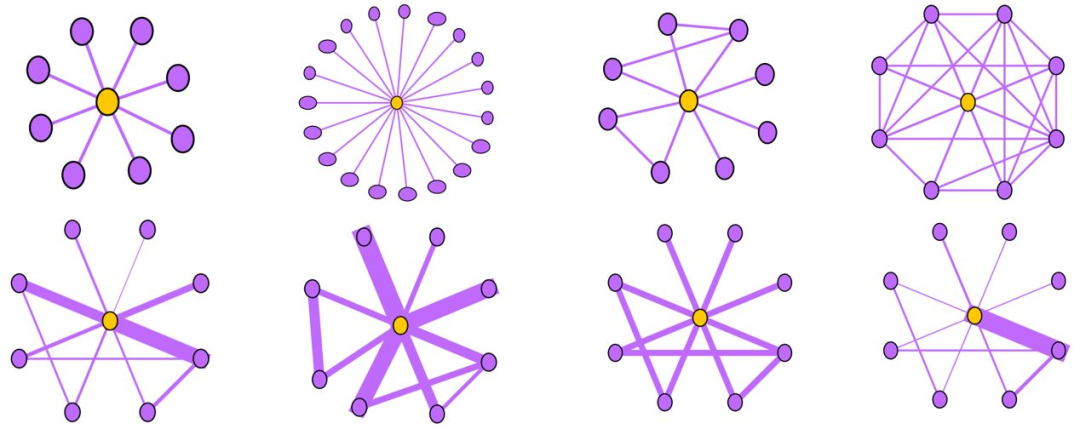
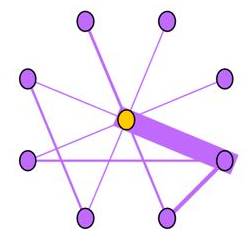
Near-Star：在正常的社交网络中，我们通常认为朋友之间可能会相互认识，因此一阶Ego-net中的邻居之间没有任何关联是非常可疑的，近似星型，邻居之间很少联系（如通话关系网络中的中介、电催人员、营销号码，他们大量的联系别人，然而联系人中之间几乎没啥联系），这种结构的Ego-net被称为star，如下图所示，中心节点与大量节点存在关联，但是邻居之间无联系或者联系很少。

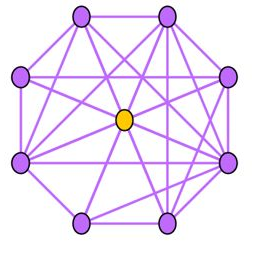
Near-Clique：与上述相反，邻居之间存在大量关联也是非常可疑的，这种结构的Ego-net被称为cliques。正如下图所示，中心节点与大量节点存在关联，邻居之间的联系非常密集，近似环状，邻居之间联系紧密（如某个讨论组、恐怖组织）。

度量方法：边数～邻居数

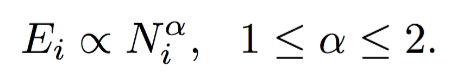
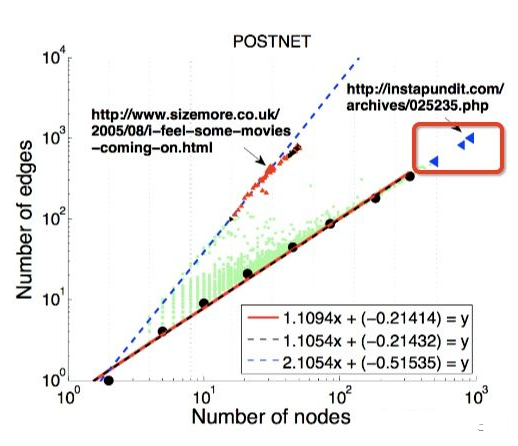
如下图所示，可以看出大多数节点Ego-net中边数 E 与邻居数 N 服从幂律分布（对数坐标后呈线性）、给定某节点i对应的 Ei 、Ni ，求出幂律系数 α ，若：

α 接近1（黑色虚线），节点i的Ego-net呈现Near-Clique 

α 接近2（蓝色虚线），节点i的Ego-net呈现Near-Star

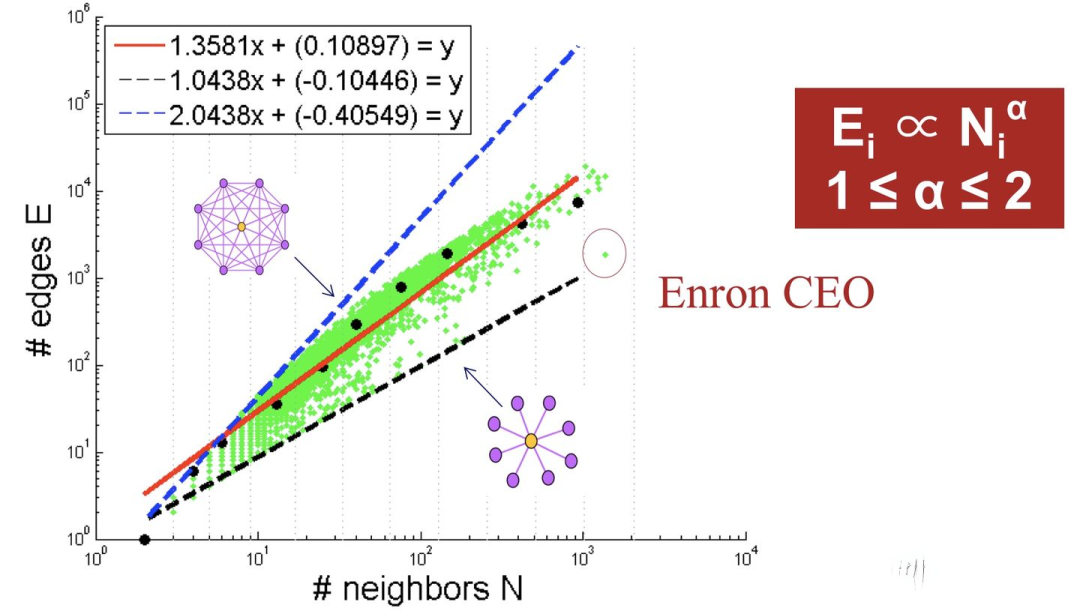红线是拟合中位数，蓝色和黑色虚线是边界线。

大多数Graph都遵循该模式：

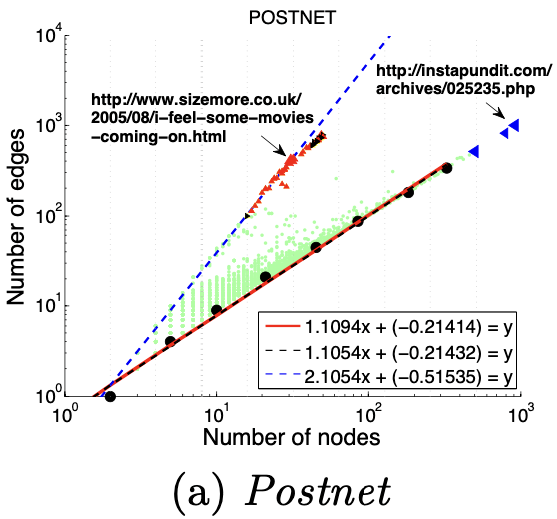
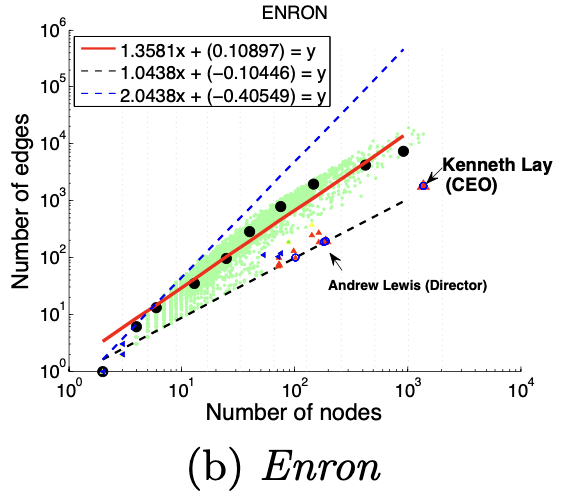
2、HeavyVicinity(权重)

HeavyVicinity指“较重的邻居“，Ego-net中边数一定时，总边权重异常大（如骗贷者通过频繁拨打电话伪造通话记录），中心节点与一小部分节点之间存在权重非常大的关联也是可疑的，如骗贷者通过频繁拨打电话伪造通话记录。正如下图所示，中心节点与少部分节点之间的连接权重非常大。

度量方法：总边权重～边数

大多数节点Ego-net中总边权重～边数也服从幂律分布（对数坐标）， β 越高表示越异常

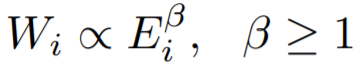
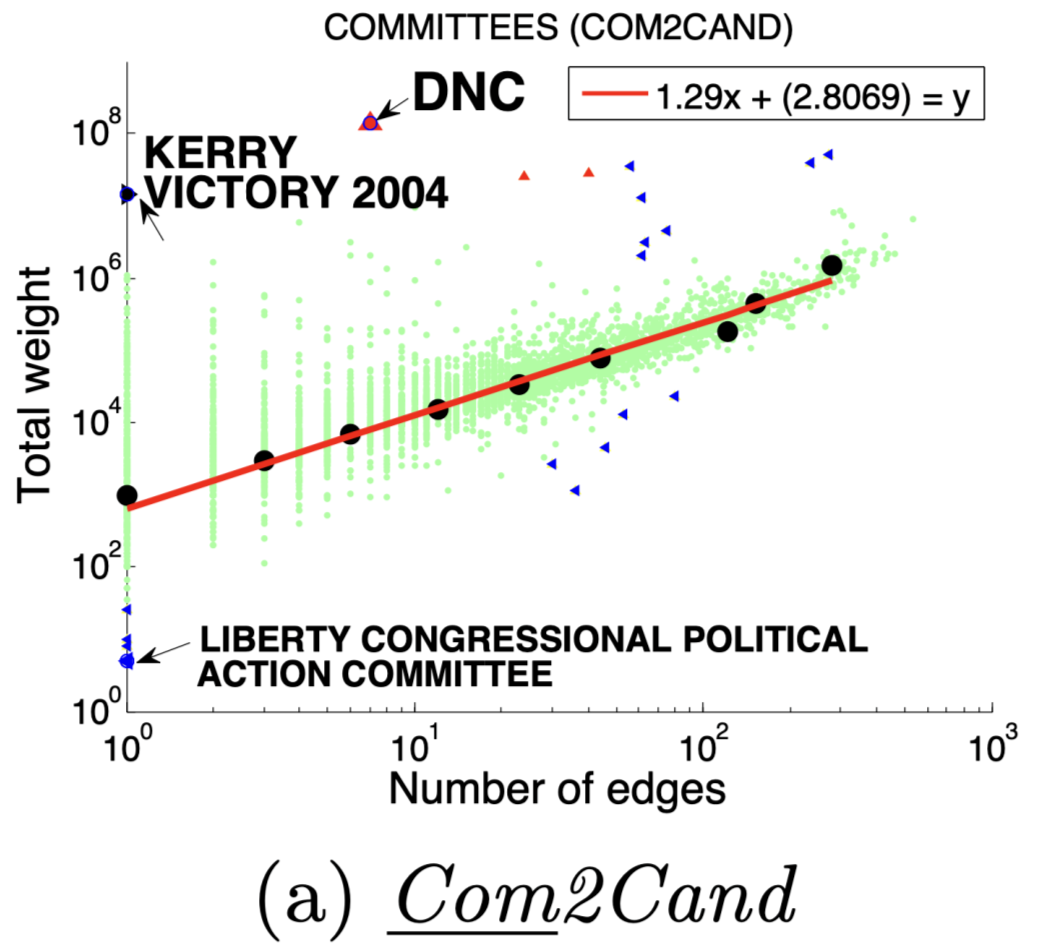
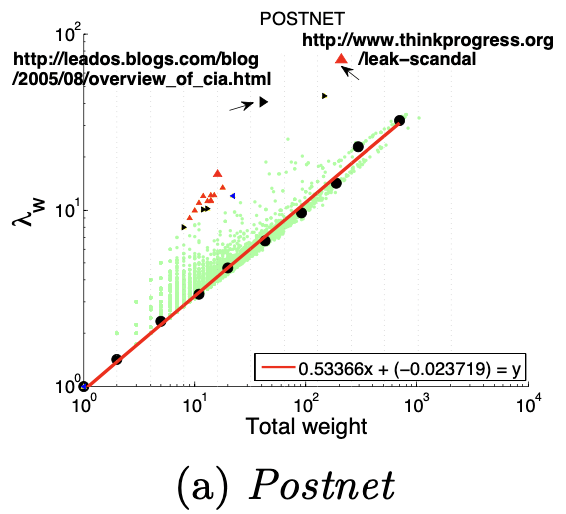
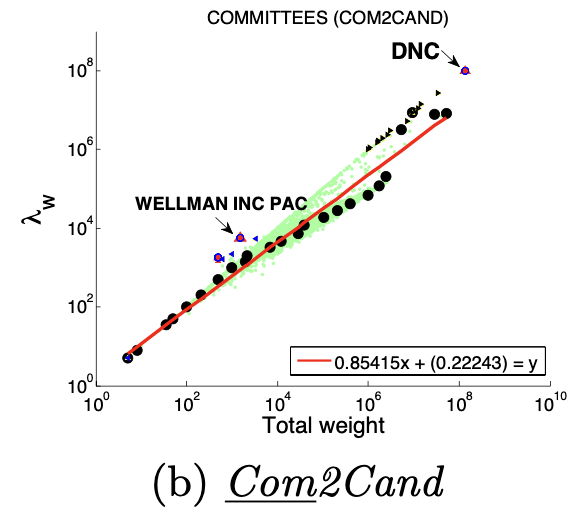
图（a）选举中，民主党（DNC）的大量的资金给为数不多的候选者

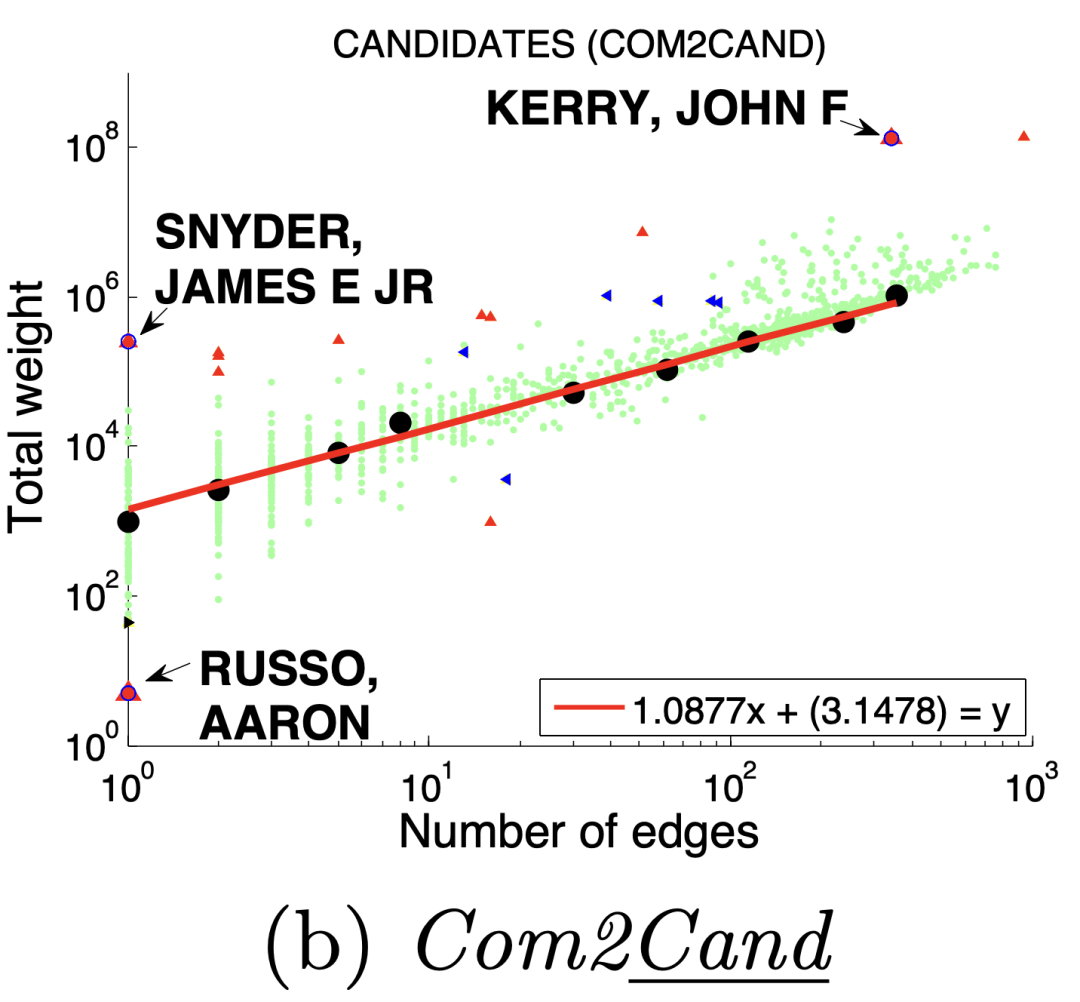
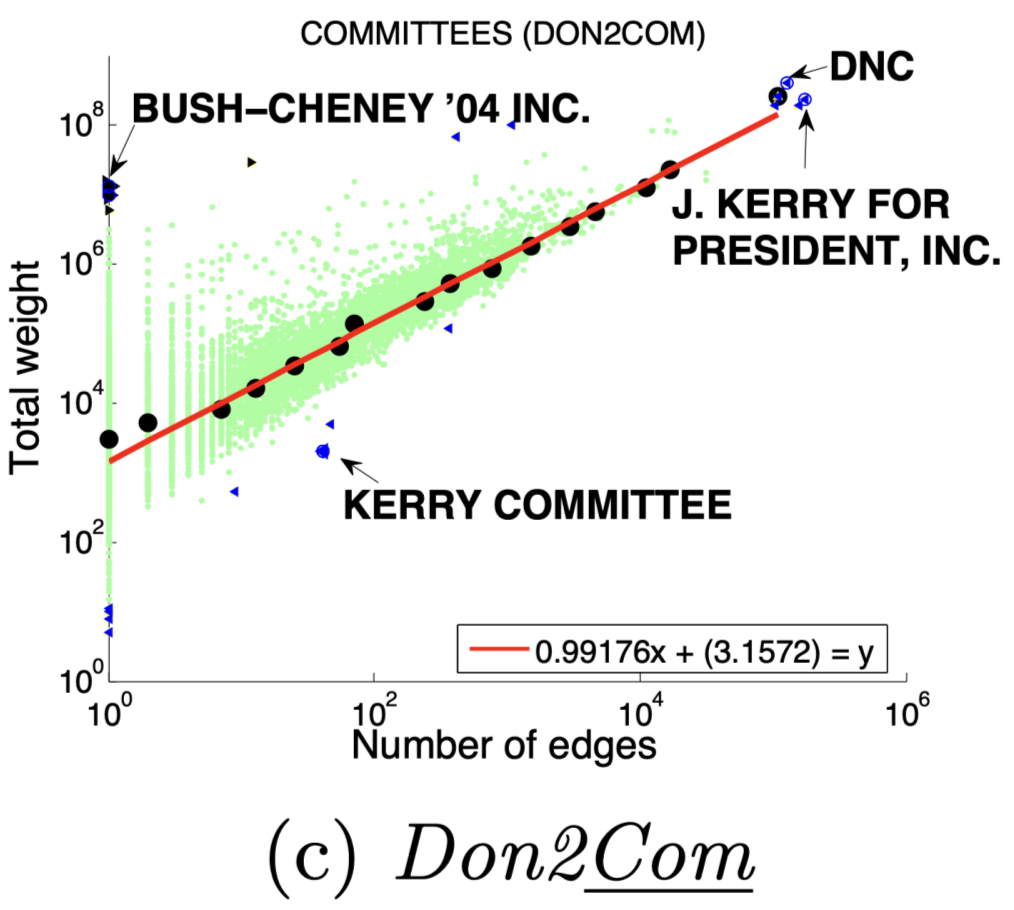
3 、DominantPair（主导边）

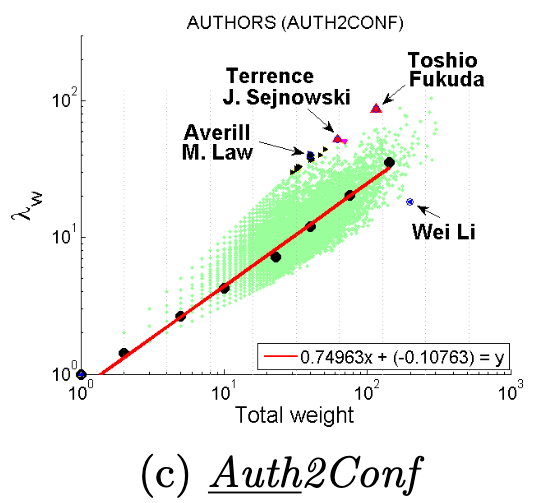
Dominant heavy links指“主导的边”，Ego-Net中存在某条边权重异常大（如学者投稿会议网络中，“Toshio Fukuda” 拥有115篇papers，投稿了17个会议，但其中87篇pager投稿了一个ICRA）：

度量方法：主特征值～总权重

大多数节点Ego-net对应带权邻接矩阵中主特征值(principal eigenvalue，即最大特征值)～总边权重也服从幂律分布，其中系数 λ 表示Ego-net中边权均匀分布， λ 接近1表示存在DominantPair的情况。

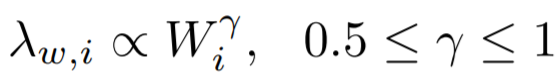
四、OddBall异常检测算法

OddBall由out-line(i)和out-lof(i)两部分组成：

out-line：计算实际点与拟合直线（红线）的偏离程度。

out-lof：但out-line但会存在“缺陷是无法识别离正常点很远，但与拟合直线很近的异常点”的缺陷,故结合传统基于密度的方法LOF（也可以选其他的）。

二者集成方式先求出两个score，然后归一化（除以最大值）后求和：

out-score(i)=out-line(i)+out-lof(i)

1、out-line

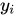• 为实际值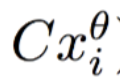， 为在拟合直线（正常点）上的预测值，二者相减为偏离程度／异常程度取

• log是为了平滑

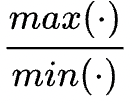•  为惩罚系数：实际值偏离正常的倍数

2、out-lof

outline的缺陷：无法识别红框内的节点，故引入LOF，详情可参考：https://zhuanlan.zhihu.com/p/28178476

五、相关思考

本文中仅考虑了节点的一阶子图，将子图范围扩展到二阶或者是更大的局部子图是否会效果更好？检测模式依赖的特征是否具有鲁棒性？