统计学知识大梳理
↑↑↑点击上方蓝字,回复资料,10个G的惊喜
前言
道德经云:”道生一,一生二,二生三,三生万物“。学习知识亦是如此,一个概念衍生出两个概念,两个概念演化出更小的子概念,接着衍生出整个知识体系。
笔者结合自己对统计学和概率论知识的理解写了这篇文章,有以下几个目标
目标一:构建出可以让人理解的知识架构,让读者对这个知识体系一览无余
目标二:尽l量阐述每个知识在数据分析工作中的使用场景及边界条件
目标三:为读者搭建从“理论”到“实践"的桥梁
概述
你的“对象” 是谁?
此对象非彼“对象”,我们学习“概率和统计学”目的在于应用到对于“对象”的研究中,笔者将我们要研究的“对象”按照维度分为了两大类。
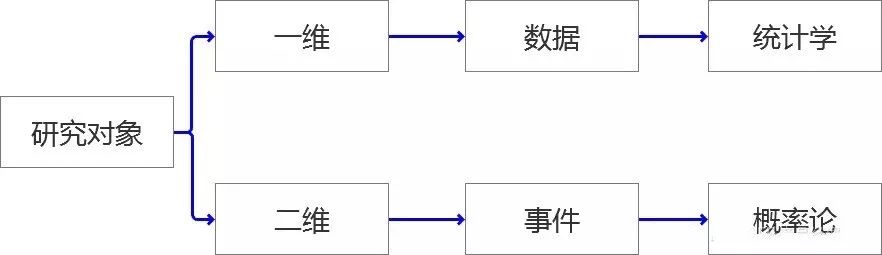
一维:就是当前摆在我们面前的“一组”,“一批”,哪怕是“一坨”数据。这里我们会用到统计学的知识去研究这类对象。
二维:就是研究某个“事件”,笔者认为事件是依托于“时间轴”存在的,过去是否发生,现在是可能会出现几种情况,每种情况未来发生的可能性有多大?这类问题是属于概率论的范畴。
因此,我们在做数据分析的研究前,先弄清我们研究的对象属于哪类范畴,然后在按着这个分支检索自己该用到的知识或方法来解决问题。
分析就像在给 “爱人” 画肖像
从外观的角度描述一个姑娘,一般是面容怎么样?身段怎么样?两个维度去描述。就像画一幅肖像画,我们的研究“对象”在描述性分析中也是通过两个维度去来描述即,“集中趋势---代表值”,“分散和程度”。
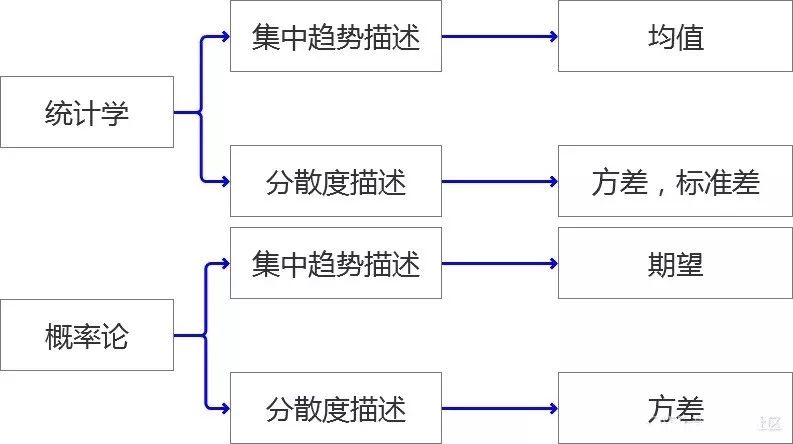
看到这几个概念是不是就很熟悉了?笔者认为一个描述性的分析就是从这两个维度来说清楚你要研究的对象是什么样子?至于从哪些特征开始说呢?就是常用的概念“均值”,“方差”之类的。下面我们进入正题,笔者将详细阐述整个知识架构。
第一部分
对“数据”的描述性分析
数据分析中最常规的情况,比如你手上有一组,一批或者一坨数据,数据分析的过程就是通过“描述”从这些数据中获取的信息,通常可以从两个维度去描述:
1. 集中趋势量度:为这批数据找到它们的“代表”
均值(μ)
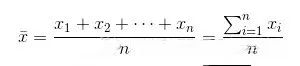
均值的局限性
均值是最常用的平均数之一,但是它的局限性在于“若用均值描述的数据中存在异常值的情况,会产生偏差” ;例如下面一组数据就不太适合用均值来代表
这5个人的年龄均值是:31.2岁

很显然,在这组数据中,大部分人的年龄是10几岁的青少年,但是E的年龄是100岁为异常值,用均值来描述他们的年龄是31.2岁,很显然用均值作为描述这组数据是不合适的,那么我们该如何准确的表征这组数据呢???
中位数
中位数,又称中点数,中值。是按顺序排列的一组数据中居于中间位置的数。
中位数的局限

回到上一个例子,若用中位数来表征这组数据的平均年龄,就变得更加合理,中位数15。
那么我们在看一下下面一组数据,中位数的表现又如何?

中位数:45
这组数据的中位数为:45,但是中位数45并不能代表这组数据。
因为这组数据分为两批,两批的差异很大。那么如何处理这类数据呢?接下来介绍第三位平均数。
众数
众数是样本观测值在频数分布表中频数最多的那一组的组中值。
平均数可以表征一批数据的典型值,但是仅凭平均数还不能给我们提供足够的信息,平均数无法表征一组数据的分散程度。
2. 分散性与变异性的量度
(全距,迷你距,四分位数,标准差,标准分)
全距=max-min
全距也叫“极差”极差。它是一组数据中最大值与最小值之差。可以用于度量数据的分散程度。
全距的局限性
全距虽然求解方便快捷,但是它的局限性在于“若数据中存在异常值的情况,会产生偏差。为了摆脱异常值带来的干扰,比如我们看一下下面的两组数据。只是增加了一个异常值,两组数据的全距产生了巨大的差异。
四分位数
所有观测值从小到大排序后四等分,处于三个分割点位置的数值就是四分位数:Q1,Q2和Q3。
Q1:第一四分位数 (Q1),又称“较小四分位数”,等于该样本中所有数值由小到大排列后第25%的数字。
Q2:第二四分位数 (Q2),又称“中位数”,等于该样本中所有数值由小到大排列后第50%的数字。
Q3:第三四分位数 (Q3),又称“较大四分位数”,等于该样本中所有数值由小到大排列后第75%的数字。
迷你距 也叫“四分位距”
迷你距。它是一组数据中较小四分位数与较大四分位数之差。
即:迷你距= 上四分位数 - 下四分位数
迷你距可以反映中间50%的数据,如果出现了极大或极小的异常值,将会被排除在中心数据50%以外。因此使用迷你距可以剔除数据中异常值。
全距,四分位距,箱形图可以表征一组数据极大和极小值之间的差值跨度,一定程度上反应了数据的分散程度,但是却无法精准的告诉我们,这些数值具体出现的频率,那么我们该如何表征呢?
我们度量每批数据中数值的“变异”程度时,可以通过观察每个数据与均值的距离来确定,各个数值与均值距离越小,变异性越小数据越集中,距离越大数据约分散,变异性越大。方差和标准差就是这么一对儿用于表征数据变异程度的概念。
方差
方差是度量数据分散性的一种方法,是数值与均值的距离的平方数的平均值。
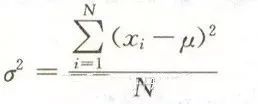
标准差
标准差为方差的开方。
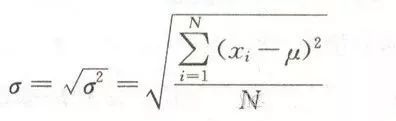
通过方差和标准差我们现在可以表征一组数据的数值的变异程度。那么对于拥有不同均值和不同标准差的多个数据集我们如何比较呢?
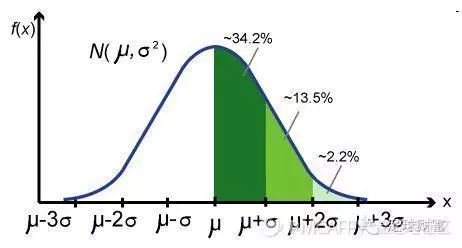
标准分——表征了距离均值的标准差的个数
标准分为我们提供了解决方法,当比较均值和标准差各不相同的数据集时,我们可以把这些数值视为来自同一个标准的数据集,然后进行比较。标准分将把每一个数据集转化为通用的分布形态,进行比较。
标准分还有个重要的作用,它可以把正态分布变为标准正态分布,后文会有介绍。
第一部分小节
1. 描述一批数据,通过集中趋势分析,找出其“代表值” ;通过分散和变异性的描述,查看这批数据的分散程度。
2. 集中趋势参数:均值,中位数,众数
3. 分散性和变异性参数 : 全距,四分位距,方差,标准差,标准分
第二部分
关于“事件”的研究分析
概率论
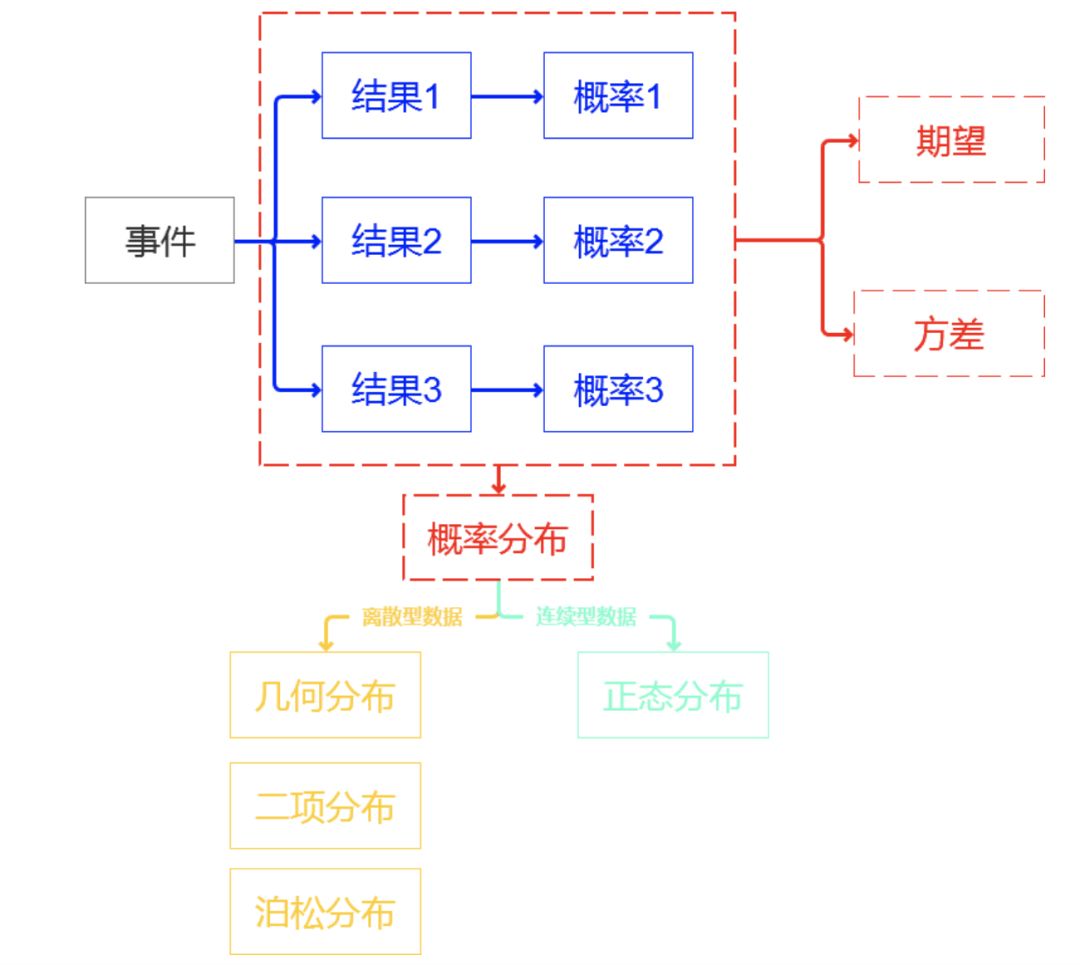
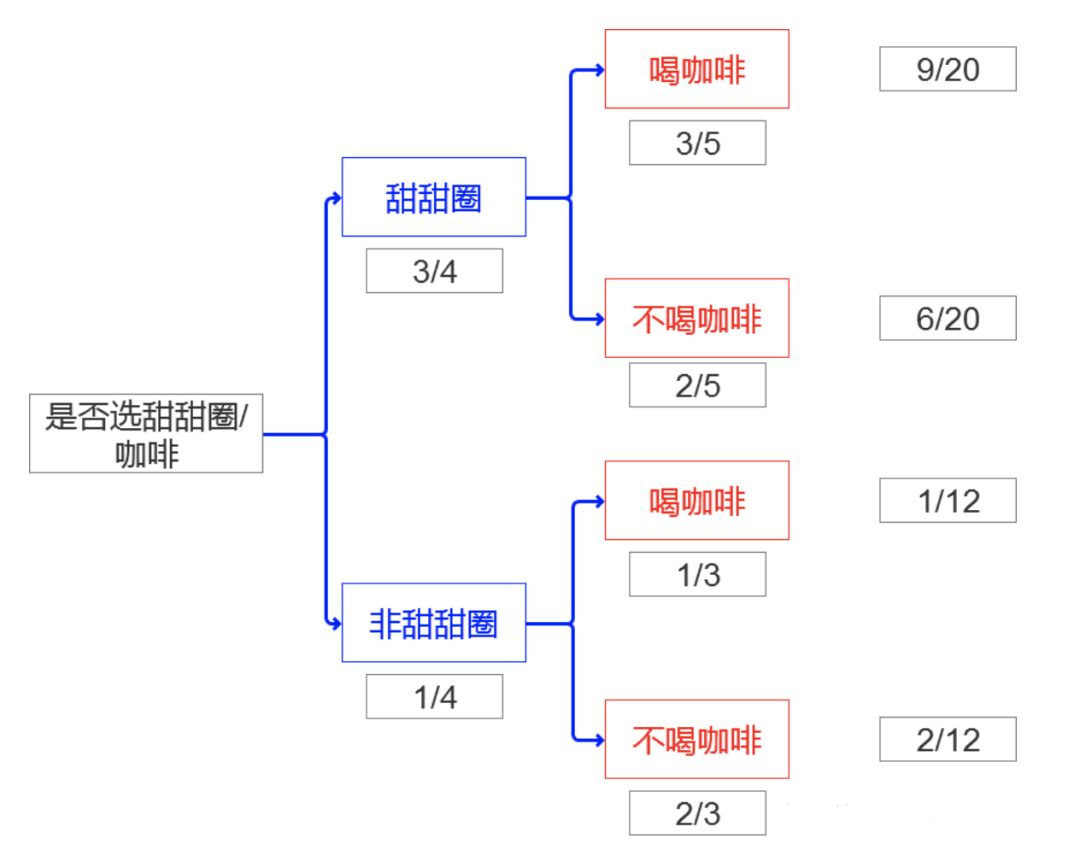
事件:有概率可言的一件事情,一个事情可能会发生很多结果,结果和结果之间要完全穷尽,相互独立。 概率:每一种结果发生的可能性。所有结果的可能性相加等于1,也就是必然!!! 概率分布:我们把事件和事件所对应的概率组织起来,就是这个事件的概率分布。
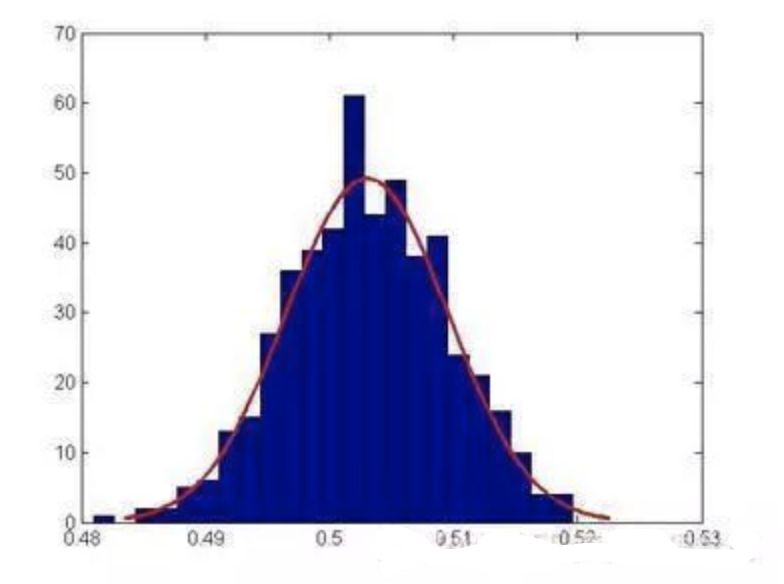

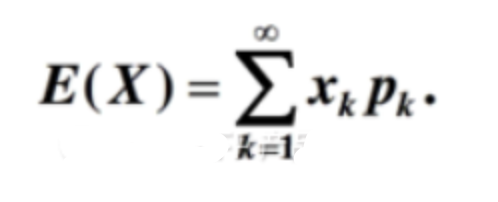
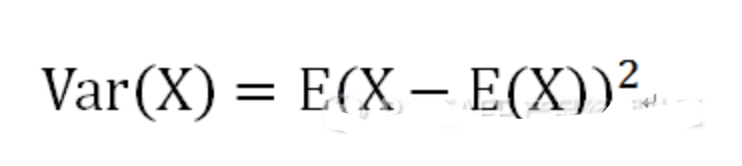
离散数据: 一个粒儿,一个粒儿的数据就是离散型数据。 连续数据: 一个串儿,一个串儿的数据就是连续型数据。

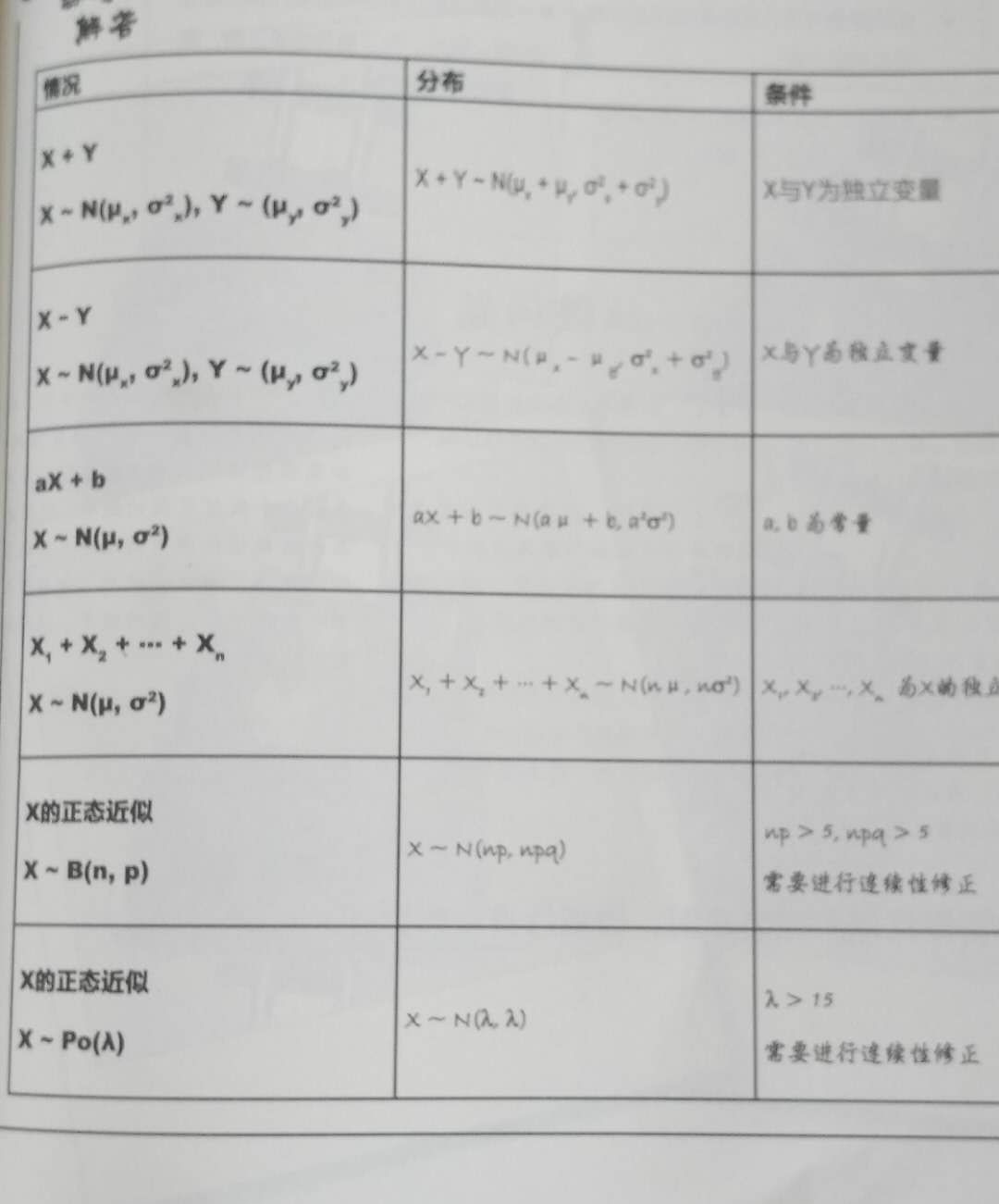
step1 --- 确定分布和范围 ,求出均值和方差 step2 --- 利用标准分将正态分布转化为标准正态分布 (还记得 第一部分的标准分吗?) step3 ---查表找概率
对立事件:如果一个事件,A’包含所有A不包含的可能性,那么我们称A’和A是互为对立事件 穷尽事件:如何A和B为穷尽事件,那么A和B的并集为1 互斥事件:如何A和B为互斥事件,那么A和B没有任何交集 独立事件:如果A件事的结果不会影响B事件结果的概率分布那么A和B互为独立事件。
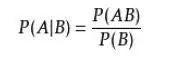
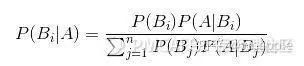
第三部分
关于“小样本”预测“大总体”

总体:你研究的所有事件的集合 样本:总体中选取相对较小的集合,用于做出关于总体本身的结论 偏倚:样本不能代表目标总体,说明该样本存在偏倚 简单随机抽样: 随机抽取单位形成样本。 分成抽样: 总体分成几组或者几层,对每一层执行简单随机抽样 系统抽样:选取一个参数K,每到第K个抽样单位,抽样一次。

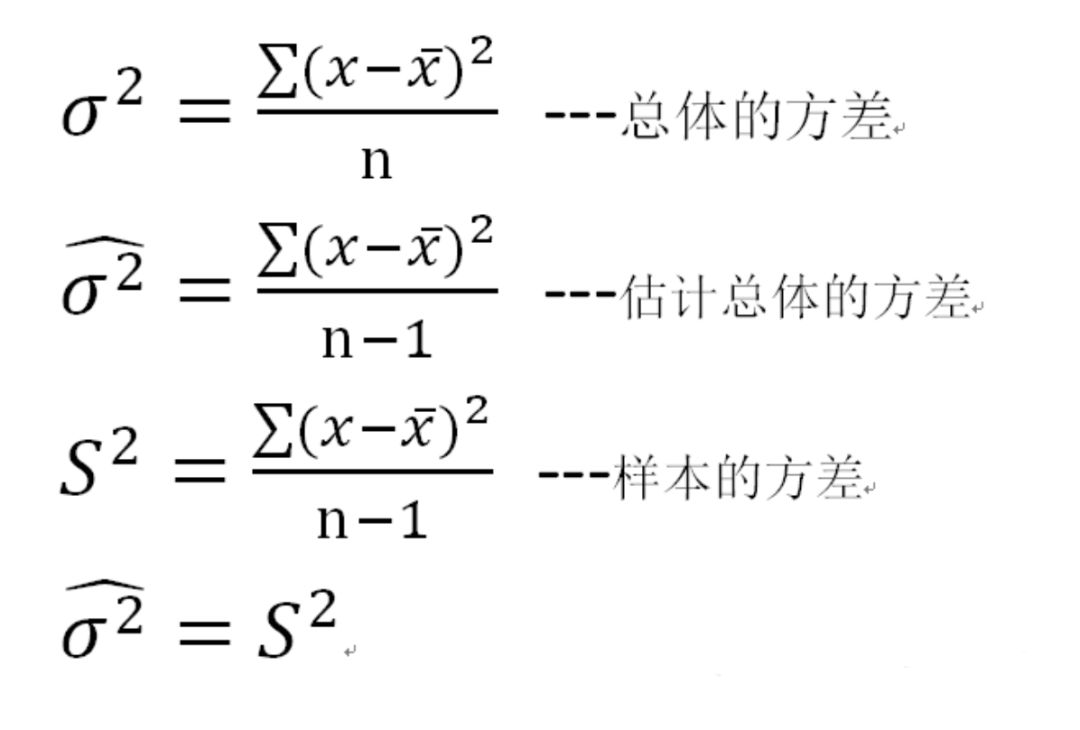

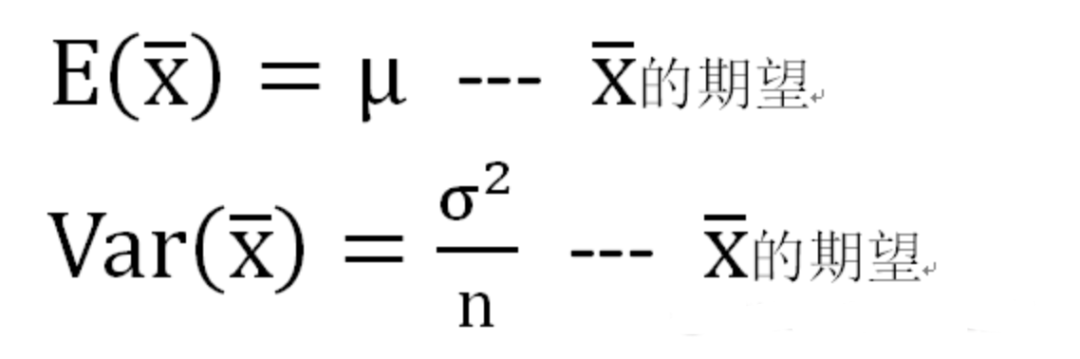
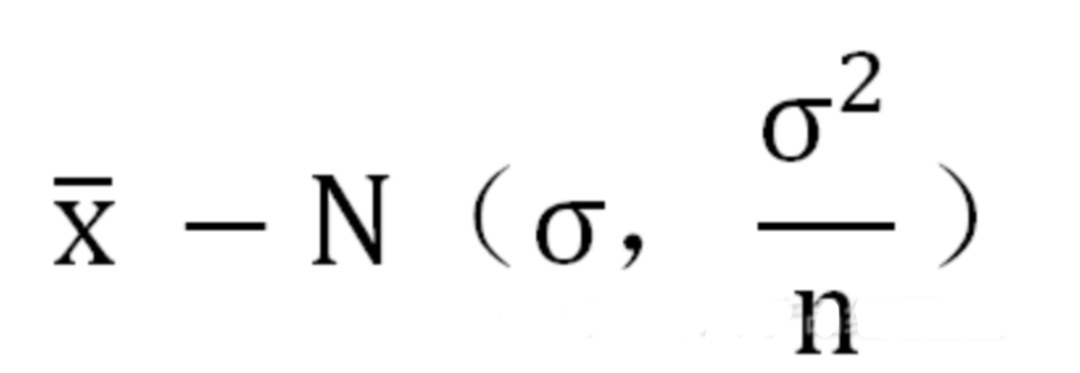

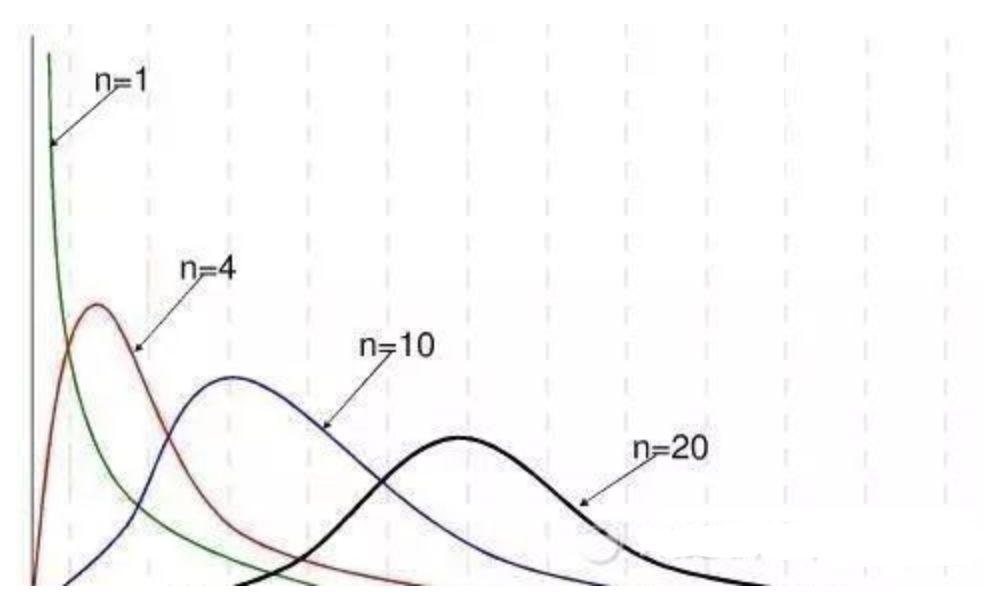
卡方分布的应用场景 用途1:用于检验拟合优度。也就是检验一组给定的数据与指定分布的吻合程度; 用途2:检验两个变量的独立性。通过卡方分布可以检查变量之间是否存在某种关联:

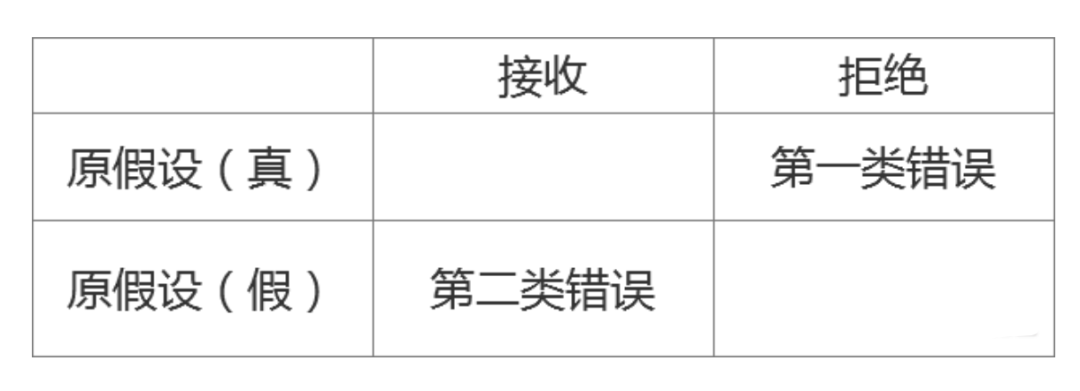
第一类错误: 拒绝了一个正确的假设,错杀了一个好人 第二类错误:接收了一个错误的假设,放过了一个坏人
第四部分
相关与回归(y=ax+b)
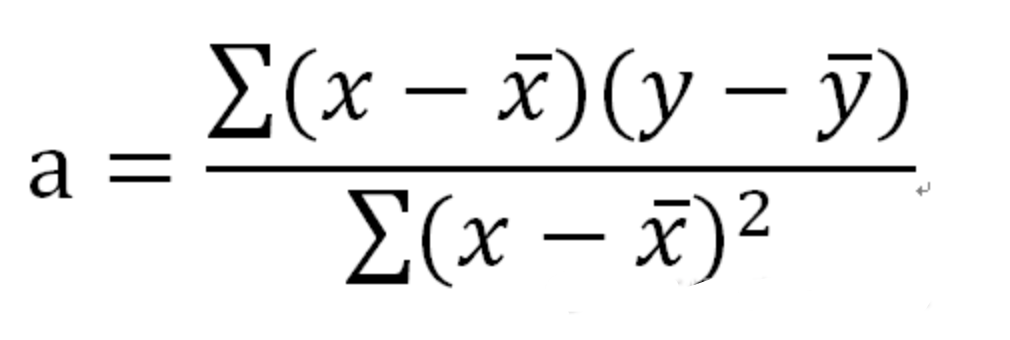
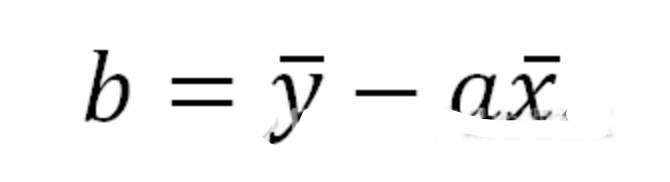
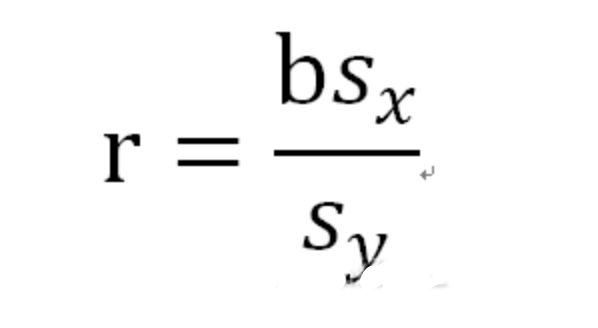
也可以加一下老胡的微信 围观朋友圈~~~
推荐阅读
(点击标题可跳转阅读)
100天搞定机器学习|Day1-62 合集 所以,机器学习和深度学习的区别是什么? 墙裂建议收藏,100道Python练手题目 老铁,三连支持一下,好吗?↓↓↓
