独家 | 每个数据科学家都应该熟悉的 5 个统计学悖论

翻译：潘玏妤

校对：赵茹萱

本文约3200字，建议阅读5分钟 本文 我们将探讨每个数据科学工作者都应该熟悉的5个统计学悖论。

摘要：统计是数据科学的一个重要部分，它为我们分析和理解数据提供了各种工具和技术。然而，有时通过统计得出的结果会违背我们的直觉，甚至自相矛盾，从而引起人们的困惑与误解。在这篇博客里，我们将探讨每个数据科学工作者都应该熟悉的5个统计学悖论。我们也将解释每个悖论是什么，为什么会发生，以及如何避免落入它的常见陷阱。读完本博客，你将对统计分析中可能出现的一些奇怪和预想之外的结果有更好的理解，从而能更好地在项目中处理它们。
目录
1.Accuracy Paradox    准确度悖论 2.False Positive Paradox    假阳性悖论 3.Gambler’s Fallacy    赌徒谬误 4.Simpson’s Paradox    辛普森悖论 5.Berkson’s Paradox    伯克森悖论 6.Conclusion    总结

1.Accuracy Paradox    准确度悖论

准确度悖论是指即使模型不具有预测性，也有可能得到具有高准确度的结果。这种情况常发生在数据集中的类的分布不平衡时。例如，给定一个数据集，其中90%的观察值属于一类，而剩下的10%属于另一类。那么预测所有观察值的多数类（majority class）的模型将有90%的准确度，即使它实际上不具备预测任何东西的能力。
接下来我们通过一个Python实例来解释上述内容：

在本例中，我们创建了一个包含两个类的不平衡数据集。它的一个类中有900个观察值（0），而另一个类中只有100个观察值（1）。然后，我们创建一个模型来预测所有观察值的多数类（0）。尽管实际上没有预测任何东西（只是一个包含1000个0的数组），这个模型达到了90%的准确度。
在医学测试中可以找到一些准确度悖论的真实案例。假设有一种患病概率为十万分之一的罕见病。如果创建了一个在检测疾病方面有99.9%准确度的测试，并将其提供给只有0.1%的患病人群，则该测试将具有99.9%的高准确率。然而，它将导致大量的假阳性（False Positive），也就是说，许多健康人将被错误地诊断为患有该疾病。
精确度和召回率在评估分类任务的表现上比准确度更好。而这两个指标（精确度和召回率）与我们下一节讨论的假阳性悖论有关。
2.False Positive Paradox    假阳性悖论

当模型具有高准确度和高假阳率时，假阳性悖论就会发生。也就是说，当大量样本实际上是阴性时，该模型可能将它们分类为阳性（即假阳。假阳率（False Positive Rate, FPR）：检测出来的假阳性样本数除以所有真实阴性样本数）。这个悖论会导致错误的结论和决策。
Python解释假阳性悖论的简单示例：

例如，想象一个病患占总人口1%的疾病的医学测试。如果该测试有99%的准确率，则它有99%的概率正确识别疾病的存在或不存在。但倘若对1000人进行检测，那么将会有10人被测出阳性，尽管事实上只有1人患病。这意味着阳性测试结果更可能是假阳性而不是真阳性。

下面是另一个针对假阳性悖论的Python代码示例：

在这种情况下，精确度和召回率是评估模型性能的更好方法。精确度评估所有阳性分类中真阳性的比例，而召回率评估所有实际阳性实例中真阳性的比例。这些措施可以帮助避免假阳性悖论，对模型性能进行更准确的评估。
3.Gambler’s Fallacy    赌徒谬误

赌徒谬误是相信过去的事件可以在随机过程中影响未来事件的概率。例如，在轮盘游戏中，一些玩家认为，如果球连续几次旋转都落在黑色上，那么下次它落在红色上的几率会更高，尽管结果依旧是随机的。
我们可以借助Python中的numpy模拟投掷一枚公平的硬币来说明这一点：

在上面的例子中，代码模拟投掷硬币10次并计算连续正面或反面的数量。赌徒谬误认为，如果连续出现了几个正面，那么下一次的结果更有可能是反面，反之亦然。然而，在现实中，硬币的每一次翻转都是独立的，并且有相同的概率产生正面或反面。
赌徒谬误会在股票市场等生活场景中出现。一些投资者可能认为，如果一只股票的价值连续几天持续上涨，之后它就更有可能下跌，尽管市场运动其实仍然是内在不可预测的，并受一系列因素的影响。
4.Simpson’s Paradox    辛普森悖论
辛普森悖论是指在一个具有某种趋势的数据集中，倘若我们把这个数据集分成许多子数据集，那么原趋势会消失或子数据集呈现的趋势与原趋势相反。如果数据被错误处理与分析，这可能会导致错误的结论。
我们通过一个例子来更好地理解这一现象。假设我们想比较一所大学男女申请者的录取率。已知我们有两个院系的数据：院系A和院系B。

在上表中，男女申请者的综合录取率为50%。但是，当我们按院系分析数据时，可以发现，在每个院系中，女性的录取率都高于男性。这似乎违背了我们的直觉，因为男性的整体录取率更高。
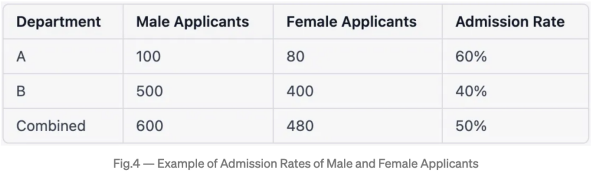
出现这种悖论是因为每个院系的申请人数和录取率都不一样。院系A整体录取率较高，但女性申请者比例较低。院系B整体录取率较低，但女性申请者比例较高。
在Python中，我们可以使用以下代码演示这个示例：

在代码中，我们用上表中的数据创建了一个dataframe，计算录取率并显示数据图表。然后计算整体录取率，得出为19.44%。最后，我们将数据按院系和性别分组，并计算每个分组的录取率。我们看到两个院系的女性录取率都较高，尽管男性的整体录取率较高。这是辛普森悖论的一个例子。
5.Berkson’s Paradox    伯克森悖论

伯克森悖论是指当两个（独立）变量之间出现/存在负相关时，如果观察由原数据分成的子数据集，这两个变量之间可能会出现正相关或无实际相关性的统计学现象。在分析中如果没考虑这两个独立变量的共因或共果，伯克森悖论就会发生。
我们将萼片长度和宽度作为两个感兴趣的变量，使用鸢尾花数据集来解释这个悖论。 首先，可以在pandas中使用corr()方法计算这两个变量之间的相关系数：

如结果所示，在整个数据集中，萼片长度和宽度之间存在负相关。
然而，如果我们按品种分割数据集并分别计算每个品种的相关系数，我们可能会得到不同的结果。比如，如果我们只考虑setosa，我们会得到一个正相关：

这意味着setosa的萼片长度和宽度之间存在正相关，这与总体负相关相反。
这种矛盾的出现是因为setosa的萼片长度和宽度的数值范围比其他品种小。因此，当我们只考虑setosa时，整个数据集内的负相关性被setosa内的正相关性所掩盖。
6.Conclusion    结论

总的来说，理解统计学悖论对数据科学家来说至关重要，因为它们可以帮助避免数据分析中的常见错误和偏见。
1. 准确度悖论告诉我们，仅仅依靠准确度不足以评估分类任务，精确度和召回率能提供更多有价值的信息； 2.假阳性悖论强调了理解假阳性相对于假阴性的重要性； 3.赌徒谬误提醒我们，每个事件都是独立的，过去的结果不会影响未来； 4.辛普森悖论表明：整体数据有可能掩盖细节变量之间的关系，从而导致错误的结论； 5.最后，伯克森悖论显示了从总体中选取非随机样本时，抽样偏差是如何发生的。

原文标题： 5 Paradoxes in Statistics Every Data Scientist Should be Familiar With 原文链接： https://pub.towardsai.net/5-paradoxes-in-statistics-every-data-scientist-should-be-familiar-with-478b74310099
编辑：王菁

译者简介

潘玏妤，流连于剧院和美术馆的CS本科生，沉迷于AI与数据科学相关学术前沿信息的古典音乐爱好者。

翻译组招募信息

工作内容： 需要一颗细致的心，将选取好的外文文章翻译成流畅的中文。如果你是数据科学/统计学/计算机类的留学生，或在海外从事相关工作，或对自己外语水平有信心的朋友欢迎加入翻译小组。

你能得到： 定期的翻译培训提高志愿者的翻译水平，提高对于数据科学前沿的认知，海外的朋友可以和国内技术应用发展保持联系，THU数据派产学研的背景为志愿者带来好的发展机遇。

其他福利： 来自于名企的数据科学工作者，北大清华以及海外等名校学生他们都将成为你在翻译小组的伙伴。

点击文末“ 阅读原文 ”加入数据派团队~

转载须知

如需转载，请在开篇显著位置注明作者和出处（转自：数据派ID：DatapiTHU），并在文章结尾放置数据派醒目二维码。有原创标识文章，请发送【文章名称-待授权公众号名称及ID】至联系邮箱，申请白名单授权并按要求编辑。

发布后请将链接反馈至联系邮箱（见下方）。未经许可的转载以及改编者，我们将依法追究其法律责任。

点击 “阅读原文” 拥抱组织