疯狂的字典
你好,我是 somenzz,Python 的灵活程度让人发指,今天来分享一下关于字典的疯狂操作,计算斐波那契数列,话不多说,先看代码:
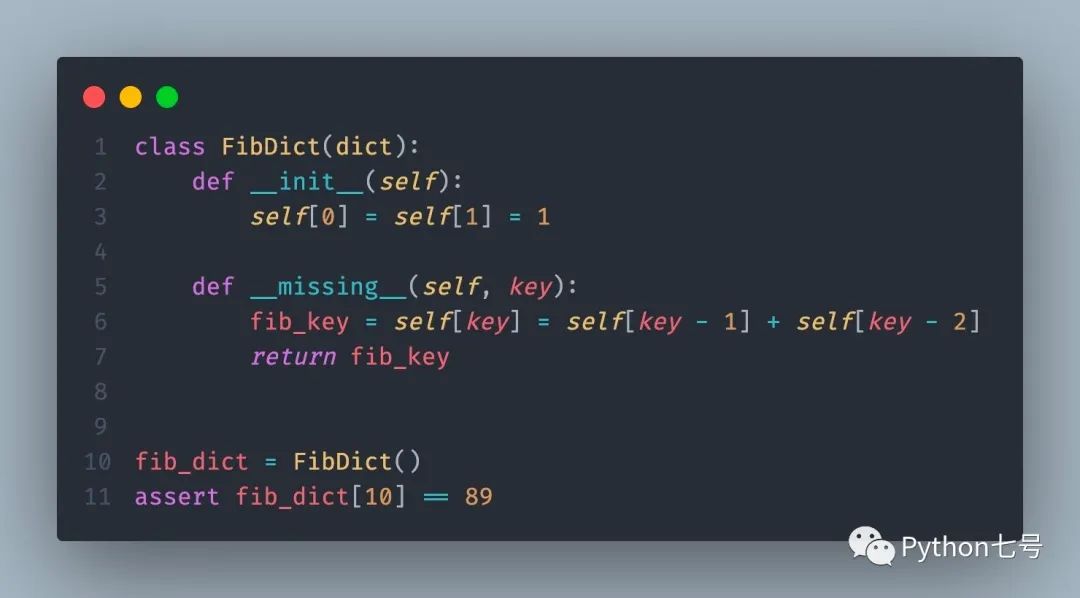
代码定义了一个类 FibDict,继承自 dict,自定义了魔术方法 __missing__ 当 dict 查找 key 失败(missing)的时候,会由 Python 解释器自行调用改方法。换句话说,如果试图从 dict 中获取不存在的 key,就会执行这个方法。
因此计算 fib_dict[10] 就会执行这个方法,计算 fib_dict[9] 和 fib_dict[8],就这样递归,一直到 fib_dict[0] 和 fib_dict[1]。
这是递归,但是字典是一种 hash 表,只要计算过的数据不会重复计算,因此效率非常高。
我们可以验证下计算 fib_dict[200] 的耗时:
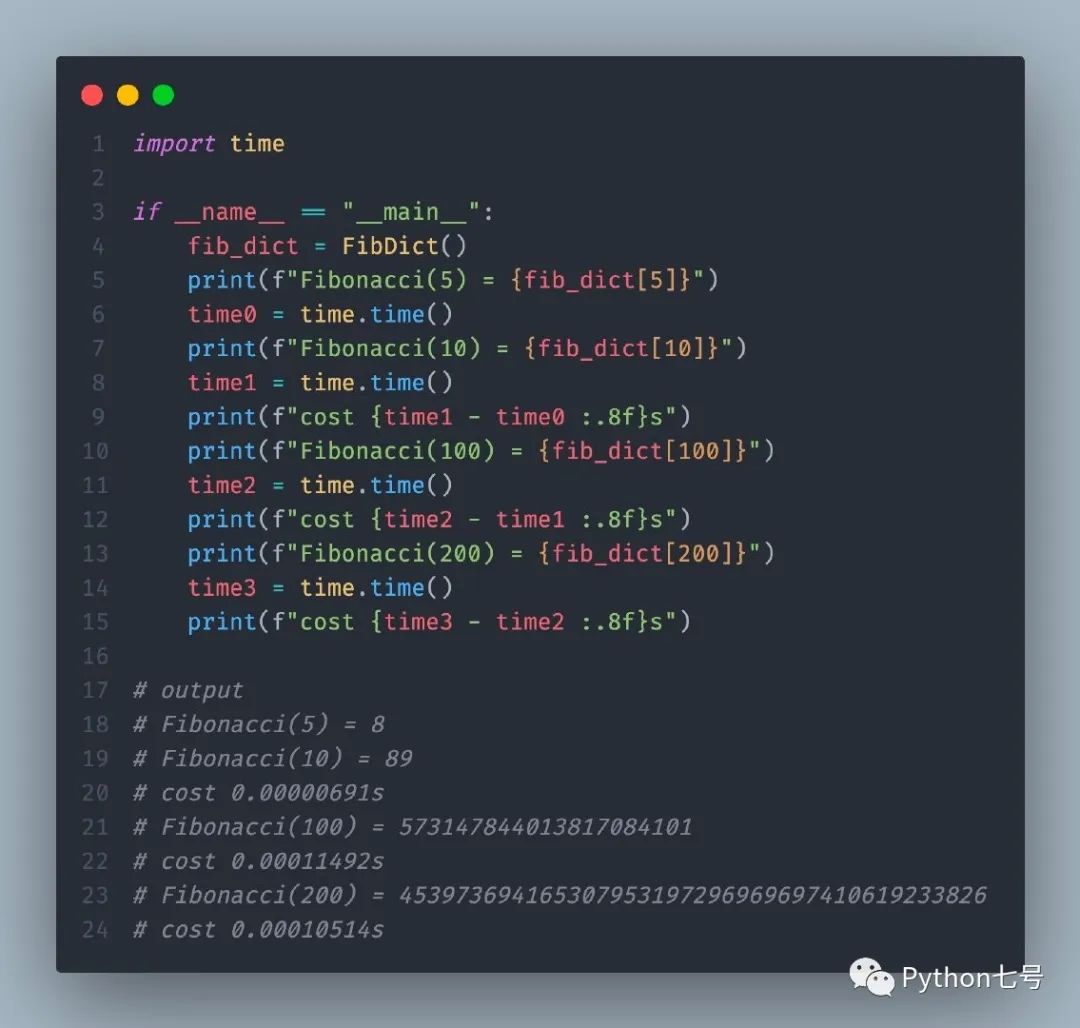
可以看出连 1 毫秒都不到。
不过,递归虽爽,可不要贪杯哦,任何事情都有极限,1000 是递归的默认极限(sys.getrecursionlimit() == 1000),如果你直接计算 fib_dict[501] 就抛出 RecursionError 异常。
你可能有个小小的疑问,为什么递归的深度是 1000,但我调用 501 次就不行了呢?其实原因在于 __missing__ 调用了 __setitem__, __setitem__ 又调用了 __missing__,因此每个缺失的 key 其实调用了两次,所以超过 500 就会报错。
但是,字典是有记忆的,如果你这样调用它,永远不会出现递归的问题: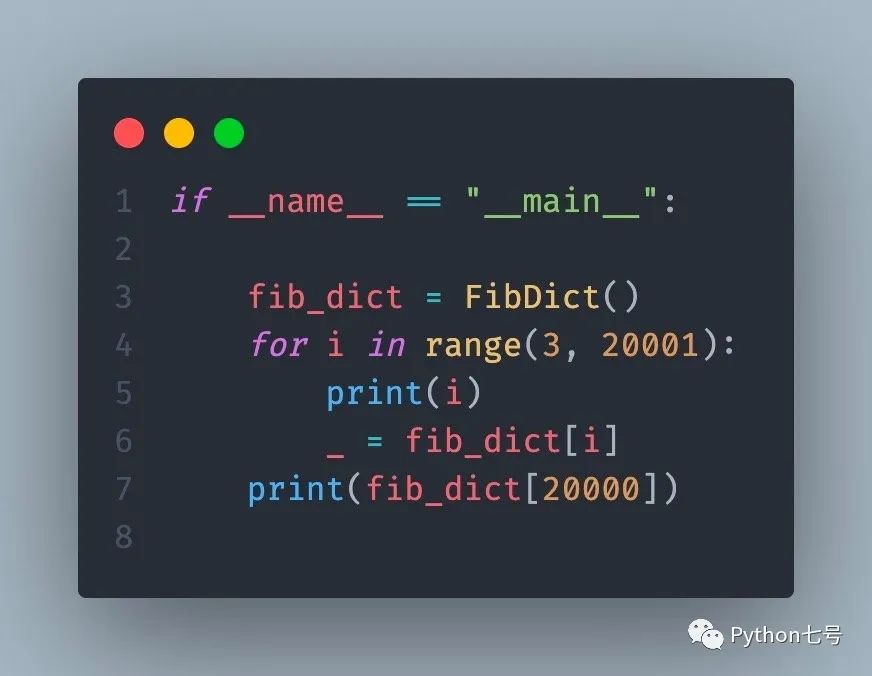
最后的话
本次分享了字典的疯狂操作,有没有让你感觉眼前一亮呢,如果有,欢迎点赞、在看、转发。点击下方的卡片或扫一扫关注我,为你提供 Python 技术支持。
推荐阅读:
评论
