R 与 Python 双语解读统计分析基础
本系列文章的主要目的是结合 R 和 Python 两种语言的代码来理解统计分析中的一些概念和方法。
主要是理解相关数学概念,不偏倚语言。为了让掌握或学习不同语言的读者都能阅读,本号特提供两种语言版本。
基本概要统计函数
分位数与经验累积分布函数 Q-Q Plot 的原理与手动实现
由于 R 语言为统计而生,所以我们把它放在前面,而 Python 放在后面压轴。R 语言有很多包可绘制统计信息,但这里主要采用 R 语言内置函数,偶然使用其他更酷的库如 ggplot2 等。
1单组数据的概要统计
这里主要看一维数组的情况,也就是单组数据。使用 R 可以很容易地计算简单的概要统计量。
先随机生成一组本篇用到的数据。
x <- rnorm(50)
x
-0.151349712210489
-0.363504035088811
-1.95206891892601
-1.59737559541699
-0.9122217288408
...
0.11816106359239
-0.940351665495342
-0.25963513375932
-0.282042226362988
1.10042202157356
注意,这里生成一个向量 x,含有服从标准正态分布的 50 个观测值。在重现该示例时,会得到不同的随机数据。因此为了保证在别的电脑也得到一样结果,这里把上面的数据存在变量 x 中。
x <- c(-0.151349712210489, -0.363504035088811, -1.95206891892601, -1.59737559541699, -0.9122217288408, -1.3196169823593, 1.05591943242618, -0.149550259852758, 0.325945279346956, -0.35441832814958, 0.351069253248304, -3.07331666453512, 0.565090710172871, -0.171040630085222, -1.46740132792868, 0.0899899556534397, 1.83621553334317, 1.81863951706006, 0.615856076199591, 0.972885619719333, -0.42872605888551, 0.106579691550742, 0.719420034087322, 0.729510556220241, 0.235267772156318, 1.73346509318415, 0.56175608734586, 0.392744047011847, -0.342050174554183, 1.07546650178172, -1.50256181287978, 1.07124607851141, -0.684037263843526, -0.622381000650786, -0.870220704569582, -0.240719319942105, -0.596954044040983, 0.00202439237435173, -1.23440595579584, 0.966331292976462, -2.17773920884933, 0.359924478034291, -0.688468404854845, -1.48419338015876, 0.980823987439883, 0.11816106359239, -0.940351665495342, -0.25963513375932, -0.282042226362988, 1.10042202157356)
# 看看前三个数据
x[1:3]
-0.151349712210489
-0.363504035088811
-1.95206891892601
一些基本的统计函数,平均值、标准差、方差以及中位数。
mean(x)
sd(x)
var(x)
median(x)
-0.121631921260524
1.05471673087863
1.11242738239531
-0.150449986031624
还可以使用函数 quantile 来获得经验分位数,如下所示。
quantile(x)
0% -3.07331666453512
25% -0.687360619602015
50% -0.150449986031624
75% 0.603164734692911
100% 1.83621553334317
如你所见,默认情况下,你将获得最小值,最大值以及 0.25、0.50 和 0.75 三个四分位数。之所以如此命名是因为它们对应于平均划分四个部分的分割点。同样,我们有十分位数 0.1、0.2,... ,0.9 以及百分位数。
第一四分位数与第三四分位数之间的差异称为四分位数间距(IQR),有时被用作标准差的可靠替代。也可以同时获得其他分位数;这可以通过添加包含所需百分比的参数来完成。例如,下面的代码就是获得十等分的方法。
pvec <- seq(0,1,0.1)quantile(x, pvec)
0% -3.07331666453512
10% -1.48603022343086
20% -0.917847716171708
30% -0.604582131023924
40% -0.306045405639466
50% -0.150449986031624
60% 0.165003747017962
70% 0.443447659112052
80% 0.776874703571486
90% 1.07166812083844
100% 1.83621553334317
请注意,经验分位数有几种可能的定义。R 中在默认参数的情况下,第 i 个观察值对应
对于上面这类基本统计函数,如果数据中缺少值,情况将变得更加复杂。为了说明,我们使用以下示例。
数据集 juul 来自 Anders Juul 进行的一项调查,该调查涉及一组健康人(主要是小学生)中的血清 IGF-I(类胰岛素生长因子)。数据集包含在 ISwR 软件包中,并且包含许多变量,这里仅使用 igf1(血清 IGF-I)。
当我们尝试计算 igf1 的平均值时会发现一个问题。
data <- read.csv('ISwR/data/juul.txt', header=TRUE, sep=' ')
dim(data)
1339,6
head(data, 3)
| age | menarche | sex | igf1 | tanner | testvol |
|---|---|---|---|---|---|
| NA | NA | NA | 90 | NA | NA |
| NA | NA | NA | 88 | NA | NA |
| NA | NA | NA | 164 | NA | NA |
mean(data$igf1)
NA
除非明确要求,否则 R 不会跳过缺失值。具有未知值的向量的平均值也是未知的。但是,你可以使用 na.rm 参数(设为不可用,相当于删除)将缺失值删除。
mean(data$igf1, na.rm=T)
340.167976424361
有一个例外: length 函数将无法理解 na.rm,因此我们无法使用它来计算 igf1 的非缺失值的数量。但是,可以使用sum(!is.na(data$igf1))。
sum(!is.na(data$igf1))
1018
可以用函数 summary 获得数字变量的摘要信息。
summary(data$igf1)
Min. 1st Qu. Median Mean 3rd Qu. Max. NA's
25.0 202.2 313.5 340.2 462.8 915.0 321
第一个和第三个是指经验四分位数(0.25 和 0.75 分位数)。实际上,可以用这个函数显示整个数据框的统计信息。
summary(data)
age menarche sex igf1
Min. : 0.170 Min. :1.000 Min. :1.000 Min. : 25.0
1st Qu.: 9.053 1st Qu.:1.000 1st Qu.:1.000 1st Qu.:202.2
Median :12.560 Median :1.000 Median :2.000 Median :313.5
Mean :15.095 Mean :1.476 Mean :1.534 Mean :340.2
3rd Qu.:16.855 3rd Qu.:2.000 3rd Qu.:2.000 3rd Qu.:462.8
Max. :83.000 Max. :2.000 Max. :2.000 Max. :915.0
NA's :5 NA's :635 NA's :5 NA's :321
tanner testvol
Min. :1.00 Min. : 1.000
1st Qu.:1.00 1st Qu.: 1.000
Median :2.00 Median : 3.000
Mean :2.64 Mean : 7.896
3rd Qu.:5.00 3rd Qu.:15.000
Max. :5.00 Max. :30.000
NA's :240 NA's :859
数据集具有月经初潮、性别和 tanner,它们被编码为数字变量,但实际上它们是分类变量。可以修改如下,
data$sex <- factor(data$sex, labels=c("M","F"))
data$menarche <- factor(data$menarche, labels=c("No","Yes"))
data$tanner <- factor(data$tanner, labels=c("I","II","III","IV","V"))
summary(data)
age menarche sex igf1 tanner
Min. : 0.170 No :369 M :621 Min. : 25.0 I :515
1st Qu.: 9.053 Yes :335 F :713 1st Qu.:202.2 II :103
Median :12.560 NA's:635 NA's: 5 Median :313.5 III : 72
Mean :15.095 Mean :340.2 IV : 81
3rd Qu.:16.855 3rd Qu.:462.8 V :328
Max. :83.000 Max. :915.0 NA's:240
NA's :5 NA's :321
testvol
Min. : 1.000
1st Qu.: 1.000
Median : 3.000
Mean : 7.896
3rd Qu.:15.000
Max. :30.000
NA's :859
注意因子变量的显示如何变化。在上面,变量 sex、menarche 和 tanner 被转换为具有适当级别名称的因子(在原始数据中,这些变量使用数字表示)。将转换后的变量放回数据框中,以替换原始变量。当然也可以使用 transform 函数,
juul <- transform(data, sex=factor(sex, labels=c("M","F")),
menarche=factor(menarche, labels=c("No","Yes")),
tanner=factor(tanner, labels=c("I","II","III","IV","V")))
summary(juul)
age menarche sex igf1 tanner
Min. : 0.170 No :369 M :621 Min. : 25.0 I :515
1st Qu.: 9.053 Yes :335 F :713 1st Qu.:202.2 II :103
Median :12.560 NA's:635 NA's: 5 Median :313.5 III : 72
Mean :15.095 Mean :340.2 IV : 81
3rd Qu.:16.855 3rd Qu.:462.8 V :328
Max. :83.000 Max. :915.0 NA's:240
NA's :5 NA's :321
testvol
Min. : 1.000
1st Qu.: 1.000
Median : 3.000
Mean : 7.896
3rd Qu.:15.000
Max. :30.000
NA's :859
2直方图
通过绘制直方图,可以对分布的形状有一个合理的印象。也就是说,计数在 x 轴上的指定划分(箱)内的观察数。
hist(x, breaks=10)
通过在 hist 调用中指定参数 breaks = n,可以在直方图中可获得 n 个矩形条。通过将 breaks 指定为向量而不是数字,则可以非均匀地控制间隔的划分。下面数据包含了一个按年龄组划分的事故率示例。这些是 0-4、5-9、10-15、16、17、18-19、20-24、25-59 和 60-79 岁年龄组的计数。可以按以下方式输入数据,
mid.age <- c(2.5, 7.5, 13, 16.5, 17.5, 19, 22.5, 44.5, 70.5)
acc.count <- c(28, 46, 58, 20, 31, 64, 149, 316, 103)
age.acc <- rep(mid.age, acc.count)
brk <- c(0, 5, 10, 16, 17, 18, 20, 25, 60, 80)
hist(age.acc, breaks=brk)
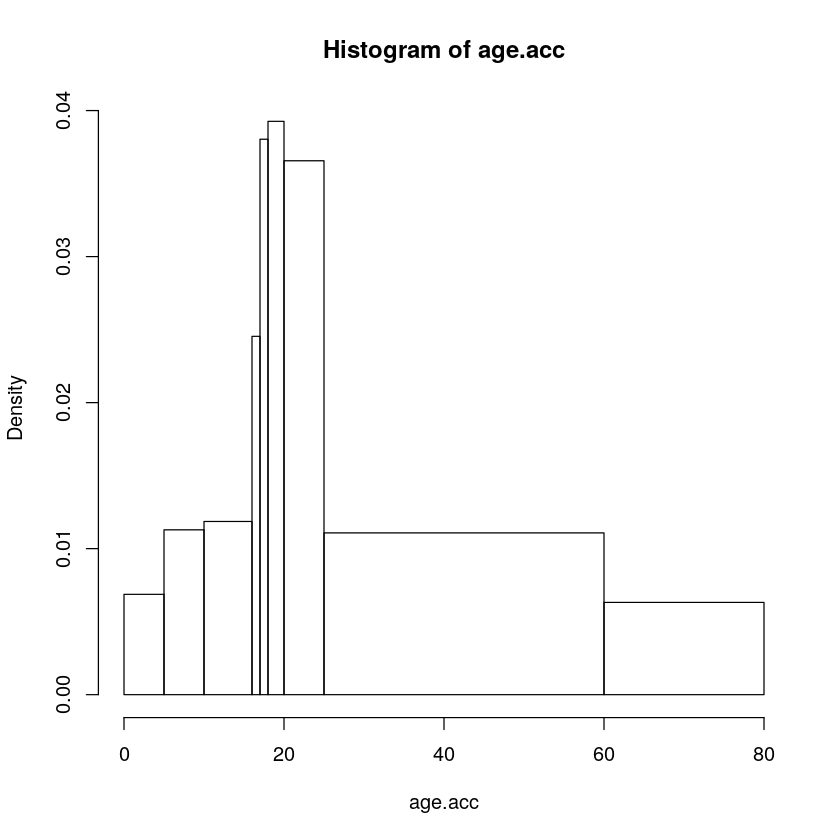
上图展示了不等距分箱的直方图,知道 Python 中该怎么绘制吗?
在这里,前三行从书中的表生成伪数据。对于每个时间间隔,将生成相应的观测值,并将年龄设置为该时间间隔的中点。也就是说,有 28 个 2.5 岁的孩子,46 个 7.5 岁的孩子,等等。然后定义了分割点的向量 brk(请注意,必须包括极端值),并将其用作 hist 的 breaks 参数,得出上图。
请注意,你会自动获得正确的直方图,其中列的面积与数字成正比。y 轴以密度单位(即每 x 单位的数据比例)为单位,因此直方图的总面积为 1。如果由于某种原因,你想要其中列高为每个间隔中的原始数字的那种直方图,则可以使用 freq = T 进行指定。对于等距断点,这是默认设置(因为这样你可以看到每列有多少个观测值),但是可以设置 freq = F 来显示密度。这实际上只是 y 轴上比例的变化,但是它的优点是可以将直方图与相应的理论密度函数叠加在一起。
3经验累积分布
经验累积分布函数定义为小于或等于 x 的数据占总数据的比例。也就是说,如果将数据从小到大排列,x 是第 k 个观测值,则小于或等于 x 的那些数占总数的比例是 k / n(如果 x 是 10 个数据中的第 7 个,则为 7/10)。上文中数据 x 的经验累积分布函数可以绘制如下。
sort(x)n <- length(x)
plot(sort(x),(1:n)/n,type="s",ylim=c(0,1),col='red')
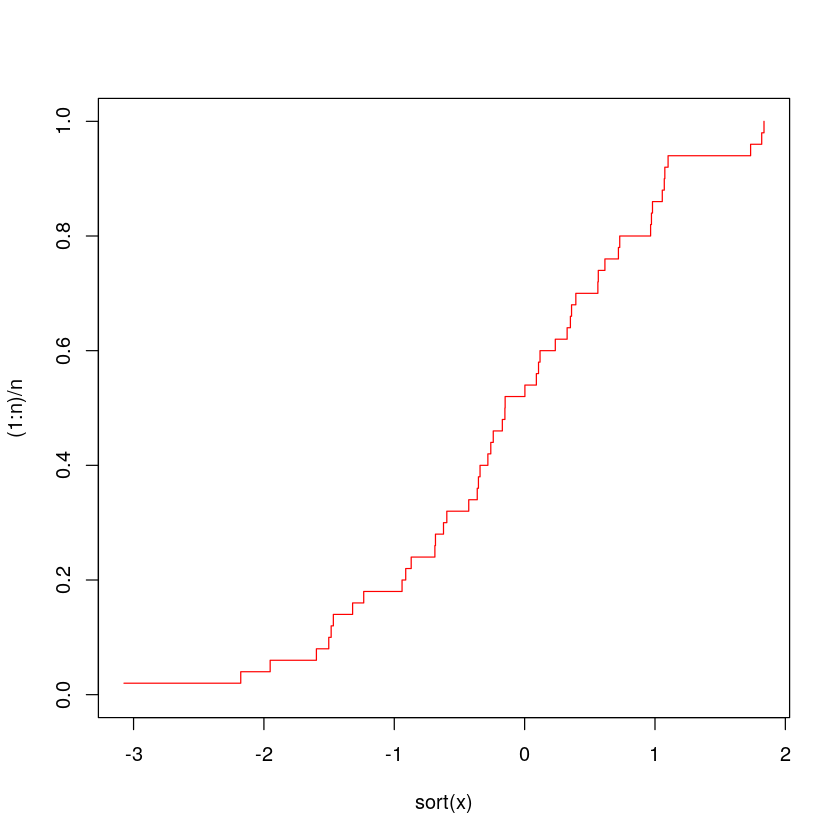
绘图参数 type ='s' 提供了一个阶梯函数,其中
可以通过设置参数 type="l" 可以看相应的折线图。下图中将两条线画在一起,结合一下横纵坐标,体会一番经验累积分布函数的涵义。
plot(sort(x),(1:n)/n,type="l",col='blue',ylim=c(0,1))+
lines(sort(x),(1:n)/n,type="s",col='red',ylim=c(0,1))
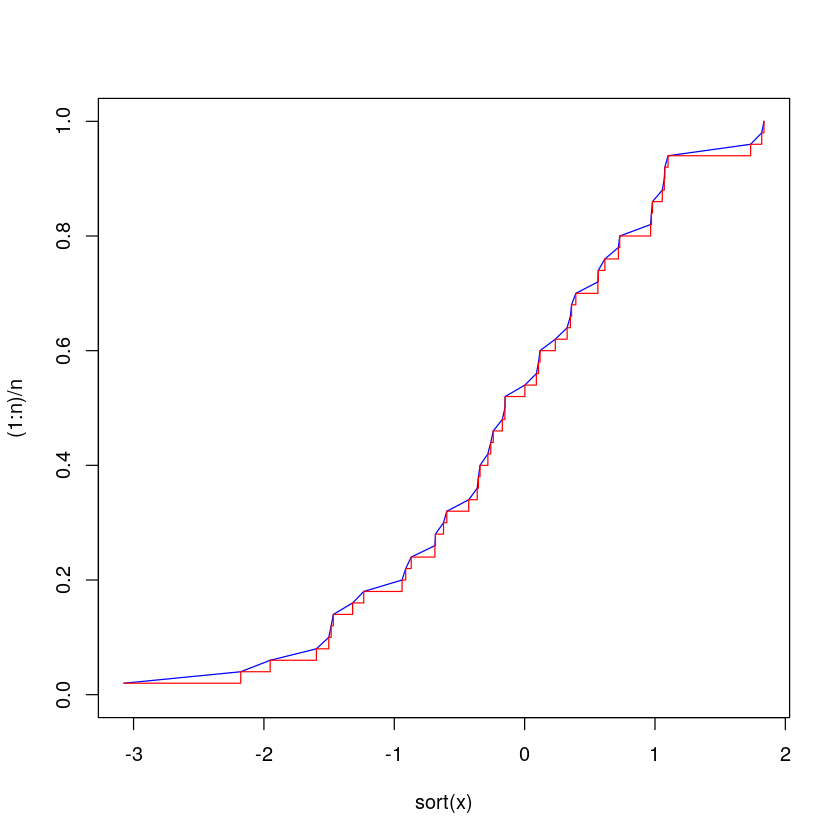
4Q-Q 图
计算经验累积分布函数(c.d.f.)的一个目的是查看是否可以假定数据为正态分布。为了更好地进行评估,你可以在标准正态分布中将第 k 个最小观测值相对于 n 个第 k 个最小观测值的期望值作图。如果数据来自某个正态分布,则你将获得一条直线。
创建这样的图貌似有点复杂。幸运的是,有一个内置的函数 qqnorm,绘制图形如下所示。
qqnorm(x)
lines(c(-2,2), c(-2,2), col='red')
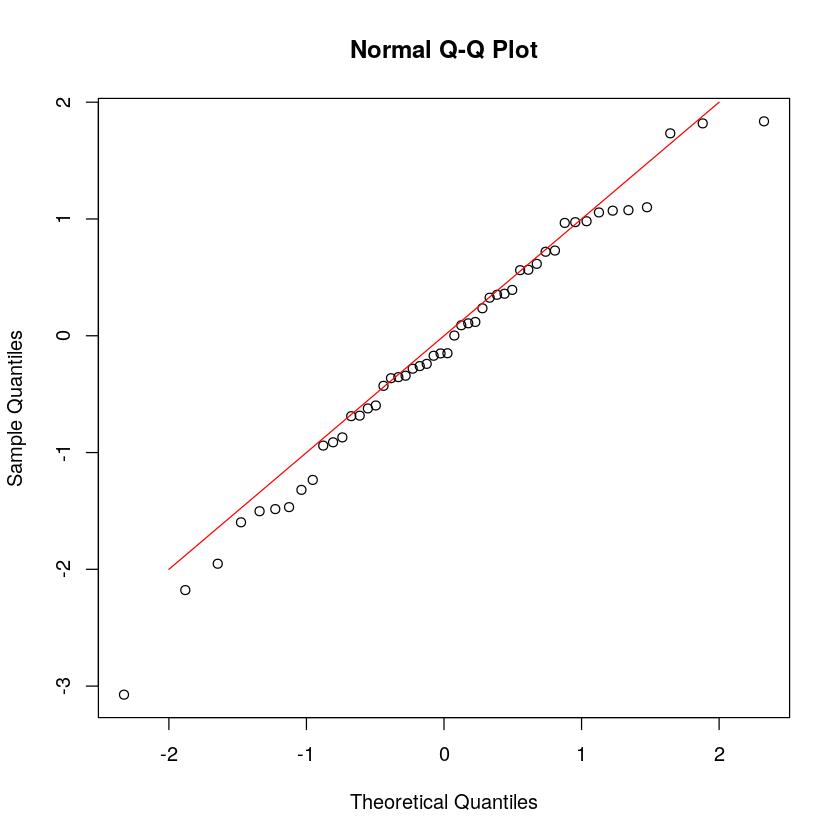
正如图的标题所示,这种图也称为Q-Q 图(分位数-分位数)。请注意,这里是沿 y 轴绘制观测值。
qqnorm(x); qqline(x, col = 2)
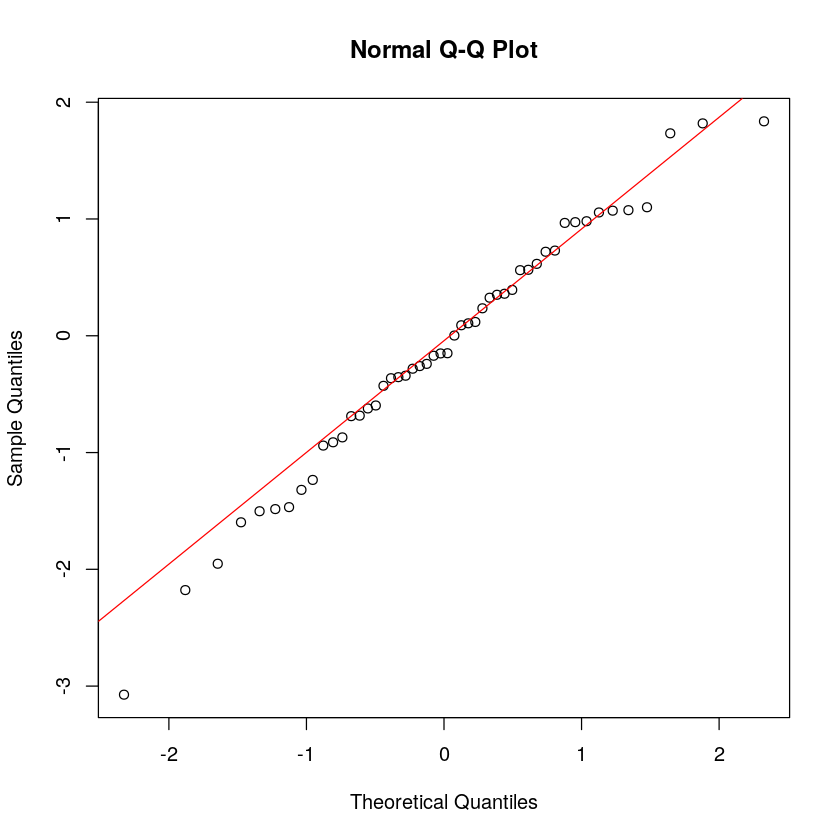
.手动实现 Q-Q Plot
为了更好地理解,我们来手动实现一下如何绘制 Q-Q Plot。
这里我们要用到累积分布函数的反函数 qnorm,即分位数函数,这里的 q 是指分位数(quantile)。使用函数 qnorm 可以回答一个问题: 标准正态分布中的某个分位数对应的 x 是多少?或者说一般正态分布的某个分位数对应的 Z-score (标准化后的 x)是多少?
比如 1 百分位数、5 百分位数、50 百分位数、95 百分位数、99 百分位数、100 百分位数对应的 x 分别为多少?可以敲如下代码,
qnorm(c(0.01, 0.05, 0.5, 0.95, 0.99, 1.0))
n <- length(x)
如果 (1:n)/n 的话,就是 2%,4%,... ,100%,那么累积分布函数的反函数 qnorm(ny) 最后那项将得到五穷大,这对于绘图有一定影响。
r <- (1:n)
ny <- r/(n)
x_norm <- qnorm(ny)
x_norm
x_sort <- sort(x)
plot(x_norm, x_sort, xlab='Theoretical Quantiles', ylab='Sample Quantiles')
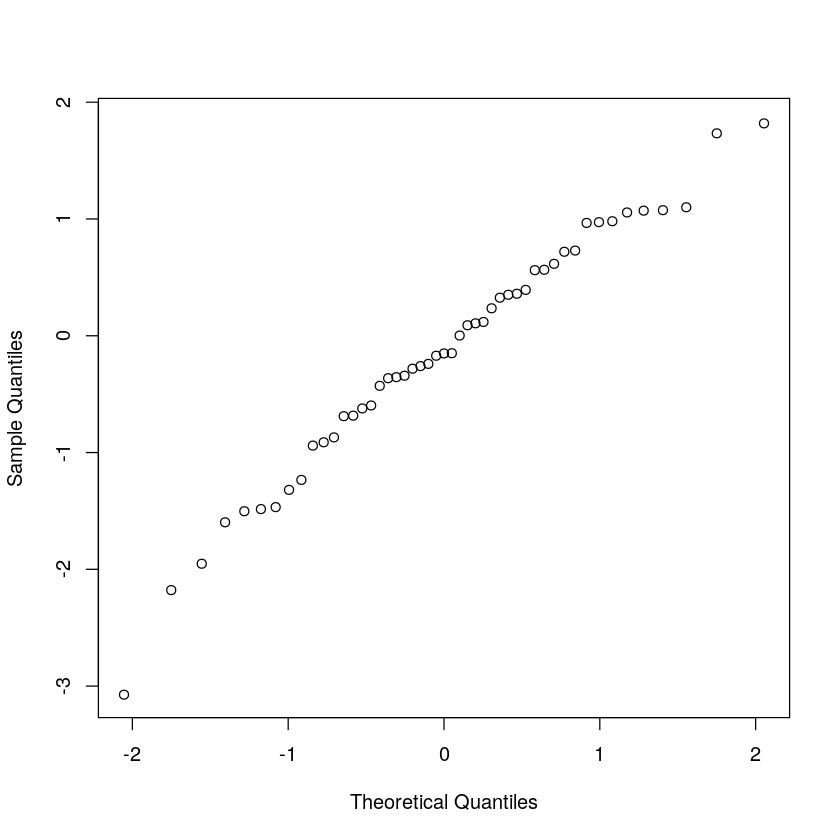
跟 R 语言内置的函数比较,可以看到右上角少了一个点啊,正是 x_norm 里最后那个 Inf。而且观察这些点的横坐标,会发现也有一些不同。我们来对这些横坐标坐个偏移 (1:n)-0.5。这样刚好相当于是 1%,3%,... ,99% 五十个百分位。
r <- (1:n)-0.5
ny <- r/(n)
x_norm <- qnorm(ny)
x_normplot(x_norm, x_sort, xlab='Theoretical Quantiles', ylab='Sample Quantiles')
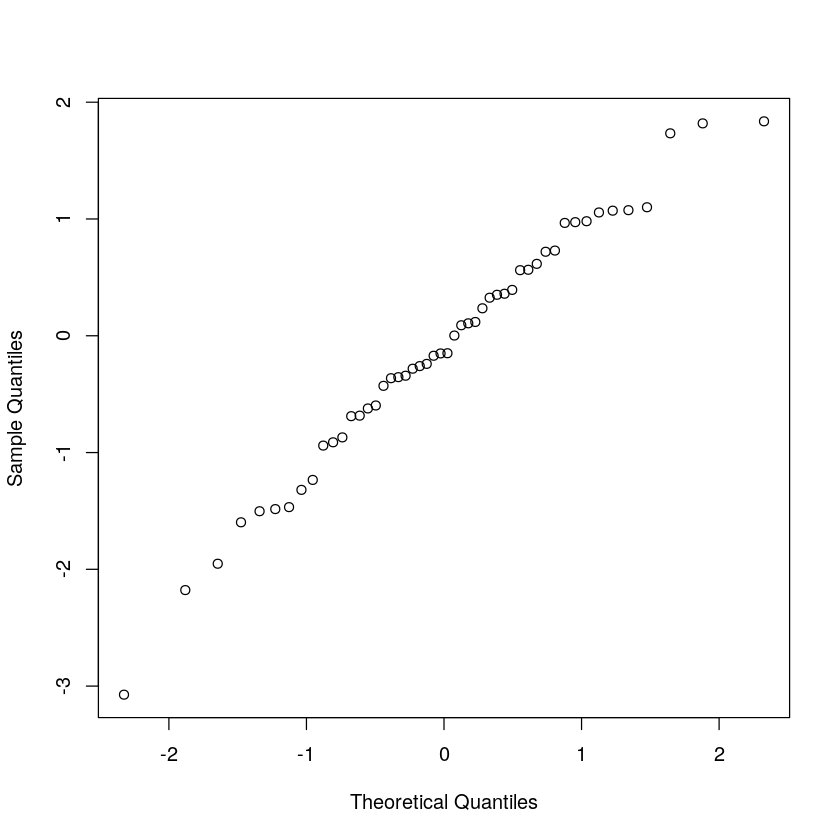
再次观察,发现与内置函数 qqnorm(x) 的结果一致。
看一下 x 和 y 都使用那组正态分布的百分位数据时的样子,
plot(x_norm, x_norm, col='red', xlab='Theoretical Quantiles', ylab='Theoretical Quantiles')
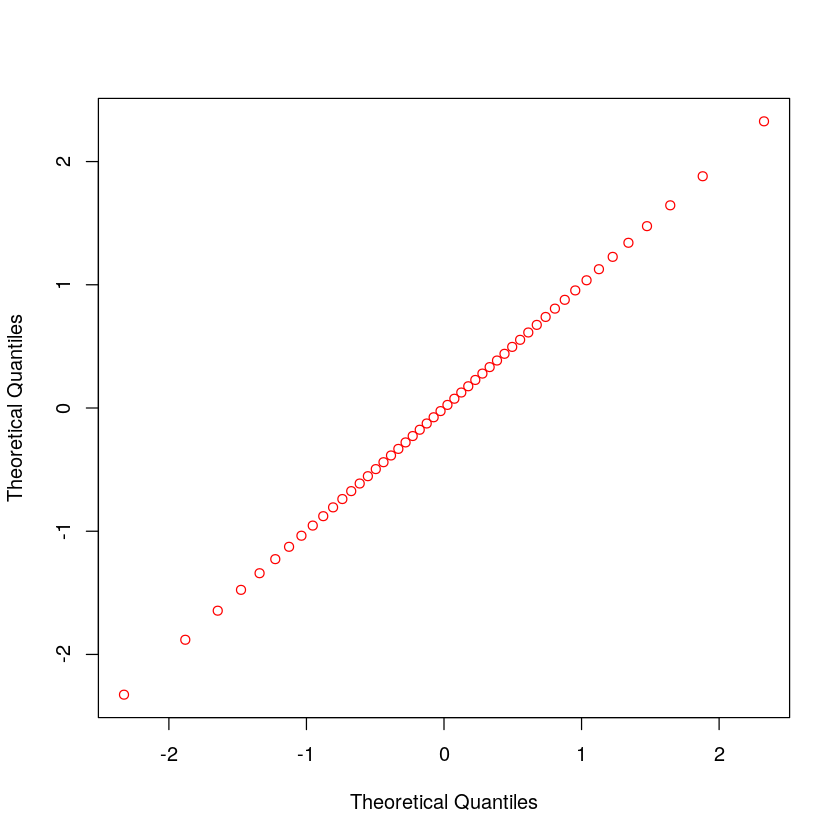
如果我们的数据遵循中间 45 度斜线,则为正态分布或接近正态分布;否则,则偏离正态分布。
让我们看一下不是正态分布时的 Q-Q Plot 的样子。
如果实际数据是来自均匀分布,我们看看此时的 Q-Q plot 会是什么样子的。
seq(x_norm[1], x_norm[50], (x_norm[50]-x_norm[1])/49)plot(x_norm, seq(x_norm[1], x_norm[50], (x_norm[50]-x_norm[1])/49), col= '#66aa66', xlab='Theoretical Quantiles', ylab='Sample Quantiles')
lines(x_norm, x_norm, type='p', col='red')
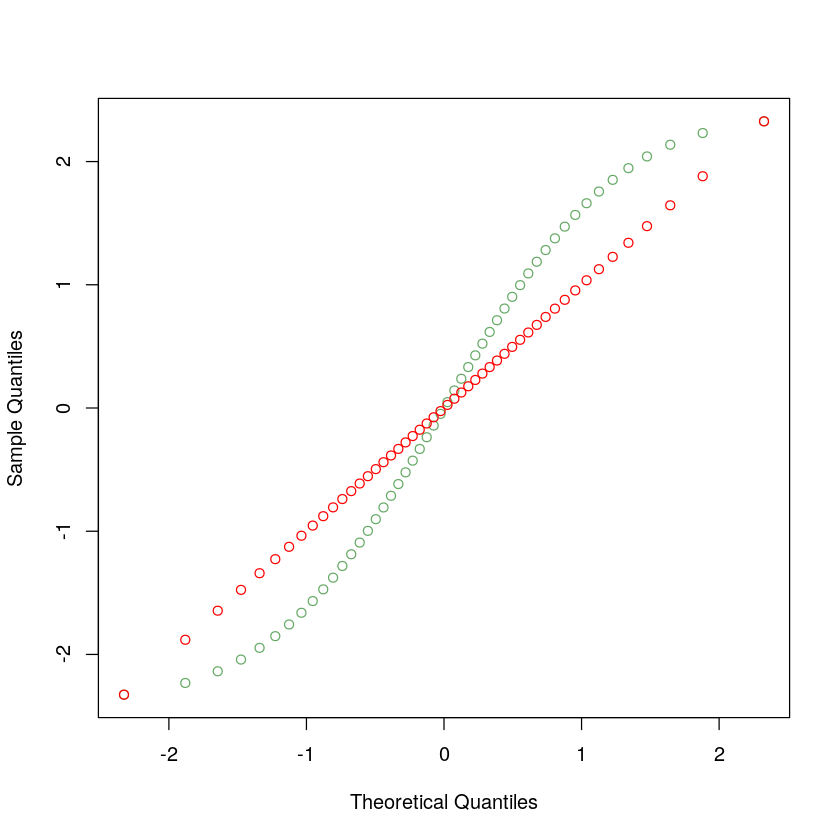
上图中红色圈圈散点图表示两个正态分布间的 Q-Q Plot,而绿色圈圈散点图是均匀分布与正态分布的 Q-Q Plot。
仔细观察这个例子,可以发现,相同百分位区间内的点如果比正态分布密集,那么那部分的点画出来比 45 度斜线平缓,如果比正态分布稀疏,画出来那部分反而更加陡峭。
5Python 版本
import numpy as np
import pandas as pd
from scipy import stats
import matplotlib.pyplot as plt
R 语言为统计而生,有很多内置统计函数,而 Python 不同,需要用第三方包来助力。
x = np.array([-0.151349712210489, -0.363504035088811, -1.95206891892601, -1.59737559541699, -0.9122217288408, -1.3196169823593, 1.05591943242618, -0.149550259852758, 0.325945279346956, -0.35441832814958, 0.351069253248304, -3.07331666453512, 0.565090710172871, -0.171040630085222, -1.46740132792868, 0.0899899556534397, 1.83621553334317, 1.81863951706006, 0.615856076199591, 0.972885619719333, -0.42872605888551, 0.106579691550742, 0.719420034087322, 0.729510556220241, 0.235267772156318, 1.73346509318415, 0.56175608734586, 0.392744047011847, -0.342050174554183, 1.07546650178172, -1.50256181287978, 1.07124607851141, -0.684037263843526, -0.622381000650786, -0.870220704569582, -0.240719319942105, -0.596954044040983, 0.00202439237435173, -1.23440595579584, 0.966331292976462, -2.17773920884933, 0.359924478034291, -0.688468404854845, -1.48419338015876, 0.980823987439883, 0.11816106359239, -0.940351665495342, -0.25963513375932, -0.282042226362988, 1.10042202157356])
pvec = np.linspace(0,1,11)
pvec
array([0. , 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1. ])
qt = np.quantile(x, pvec)
qt[:,None]
array([[-3.07331666],
[-1.48603022],
[-0.91784772],
[-0.60458213],
[-0.30604541],
[-0.15044999],
[ 0.16500375],
[ 0.44344766],
[ 0.7768747 ],
[ 1.07166812],
[ 1.83621553]])
data = pd.read_csv('ISwR/data/juul.txt', sep=' ')
data
| age | menarche | sex | igf1 | tanner | testvol | |
|---|---|---|---|---|---|---|
| 0 | NaN | NaN | NaN | 90.0 | NaN | NaN |
| 1 | NaN | NaN | NaN | 88.0 | NaN | NaN |
| 2 | NaN | NaN | NaN | 164.0 | NaN | NaN |
| 3 | NaN | NaN | NaN | 166.0 | NaN | NaN |
| 4 | NaN | NaN | NaN | 131.0 | NaN | NaN |
| ... | ... | ... | ... | ... | ... | ... |
| 1334 | 60.99 | 2.0 | 2.0 | 226.0 | 5.0 | NaN |
| 1335 | 62.73 | 2.0 | 2.0 | NaN | NaN | NaN |
| 1336 | 65.00 | 2.0 | 2.0 | 106.0 | NaN | NaN |
| 1337 | 67.88 | 2.0 | 2.0 | 217.0 | NaN | NaN |
| 1338 | 75.12 | 2.0 | 2.0 | 135.0 | NaN | NaN |
count = data['igf1'].isna().sum()
count
321
count = data['igf1'].isnull().sum()
count
321
data['igf1'].mean()
340.1679764243615
data['igf1'].describe()
count 1018.000000
mean 340.167976
std 171.035599
min 25.000000
25% 202.250000
50% 313.500000
75% 462.750000
max 915.000000
Name: igf1, dtype: float64
查看整个数据框的统计摘要信息。
data.describe()
| age | menarche | sex | igf1 | tanner | testvol | |
|---|---|---|---|---|---|---|
| count | 1334.000000 | 704.000000 | 1334.000000 | 1018.000000 | 1099.000000 | 480.000000 |
| mean | 15.095352 | 1.475852 | 1.534483 | 340.167976 | 2.639672 | 7.895833 |
| std | 11.252877 | 0.499772 | 0.498997 | 171.035599 | 1.763140 | 8.212571 |
| min | 0.170000 | 1.000000 | 1.000000 | 25.000000 | 1.000000 | 1.000000 |
| 25% | 9.052500 | 1.000000 | 1.000000 | 202.250000 | 1.000000 | 1.000000 |
| 50% | 12.560000 | 1.000000 | 2.000000 | 313.500000 | 2.000000 | 3.000000 |
| 75% | 16.855000 | 2.000000 | 2.000000 | 462.750000 | 5.000000 | 15.000000 |
| max | 83.000000 | 2.000000 | 2.000000 | 915.000000 | 5.000000 | 30.000000 |
6直方图
plt.figure(figsize=(9, 5))
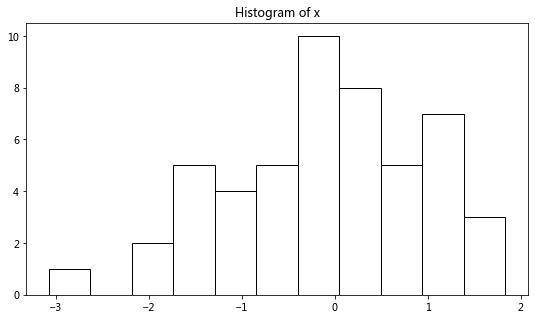
plt.hist(x, bins=11, color='w', edgecolor='k')
plt.title('Histogram of x');
mid_age = np.array([2.5, 7.5, 13, 16.5, 17.5, 19, 22.5, 44.5, 70.5])
acc_count = np.array([28, 46, 58, 20, 31, 64, 149, 316, 103])
age_acc = np.repeat(mid_age, acc_count)
age_acc.shape
(815,)
plt.figure(figsize=(9, 5))
brk = np.array([0, 5, 10, 16, 17, 18, 20, 25, 60, 80])
plt.hist(age_acc, bins=brk, color='w', edgecolor='k', density=True)
(array([0.00687117, 0.01128834, 0.01186094, 0.02453988, 0.03803681,
0.0392638 , 0.03656442, 0.011078 , 0.00631902]),
array([ 0, 5, 10, 16, 17, 18, 20, 25, 60, 80]),
)
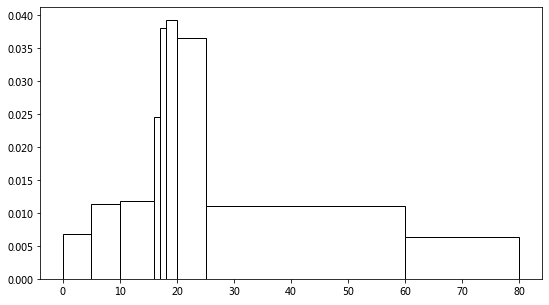
.经验累积分布函数与 Q-Q Plot
x = np.array([-0.151349712210489, -0.363504035088811, -1.95206891892601, -1.59737559541699, -0.9122217288408, -1.3196169823593, 1.05591943242618, -0.149550259852758, 0.325945279346956, -0.35441832814958, 0.351069253248304, -3.07331666453512, 0.565090710172871, -0.171040630085222, -1.46740132792868, 0.0899899556534397, 1.83621553334317, 1.81863951706006, 0.615856076199591, 0.972885619719333, -0.42872605888551, 0.106579691550742, 0.719420034087322, 0.729510556220241, 0.235267772156318, 1.73346509318415, 0.56175608734586, 0.392744047011847, -0.342050174554183, 1.07546650178172, -1.50256181287978, 1.07124607851141, -0.684037263843526, -0.622381000650786, -0.870220704569582, -0.240719319942105, -0.596954044040983, 0.00202439237435173, -1.23440595579584, 0.966331292976462, -2.17773920884933, 0.359924478034291, -0.688468404854845, -1.48419338015876, 0.980823987439883, 0.11816106359239, -0.940351665495342, -0.25963513375932, -0.282042226362988, 1.10042202157356])
x_sort = np.sort(x)
ys = (np.arange(x.shape[0])+0.5)/x.shape[0]
ys
array([0.01, 0.03, 0.05, 0.07, 0.09, 0.11, 0.13, 0.15, 0.17, 0.19, 0.21,
0.23, 0.25, 0.27, 0.29, 0.31, 0.33, 0.35, 0.37, 0.39, 0.41, 0.43,
0.45, 0.47, 0.49, 0.51, 0.53, 0.55, 0.57, 0.59, 0.61, 0.63, 0.65,
0.67, 0.69, 0.71, 0.73, 0.75, 0.77, 0.79, 0.81, 0.83, 0.85, 0.87,
0.89, 0.91, 0.93, 0.95, 0.97, 0.99])
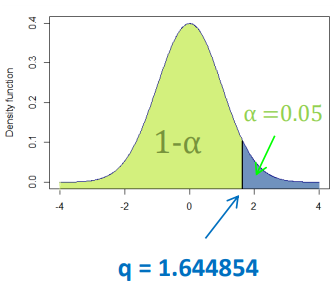
我们可以使用 stats.norm.ppf 函数来计算正态分布的百分位数。如 95 百分位数可以如下计算,
norm.ppf(0.95, loc=0, scale=1)
1.6448536269514722
参见下图,密度函数的蓝色部分面积为 0.05。
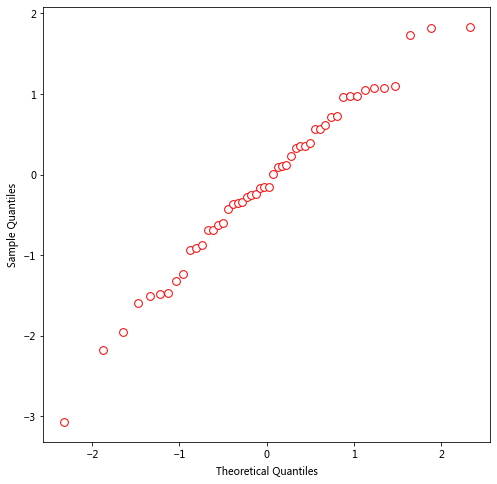
x_norm = stats.norm.ppf(ys)
plt.figure(figsize=(8, 8))
plt.scatter(x_norm, x_sort, s=60, color='w', edgecolors='red');
plt.xlabel('Theoretical Quantiles')
plt.ylabel('Sample Quantiles')
⟳参考资料⟲
