「类别型」特征分析方法总结-轻识

本文系统梳理了9种类别型特征的编码方法。如有不足，还望指正。

一、背景

当我们预处理数据时，碰到类别型变量，需要将它们编码转换后才能输入进模型当中。按照不同的划分标准，类别型变量有：

● 按照类别是否有序：有序和无序的类别特征。

● 按照类别数量：高基类和低基类的类别特征。

针对不同的类别特征和任务，可选的类别特征编码方法也不一样。本文主要介绍常见且好用的类别编码方法，希望对大家有所帮助。

二、方法

1. 标签编码（Label Encoder）

标签编码就是简单地赋予不同类别，不同的数字标签。属于硬编码，优点是简单直白，网上很多说适用于有序类别型特征，不过如果是分类任务且类别不多的情况下，LGBM只要指定categorical_feature也能有较好的表现。但不建议用在高基类特征上，而且标签编码后的自然数对于回归任务来说是线性不可分的。

from sklearn.preprocessing import LabelEncoderle = LabelEncoder()x = ['male', 'female', 'male']x_trans = le.fit_transform(x)
>>>x_transarray([1, 0, 1], dtype=int64)

2. 哈希编码（Hash Encoder）

哈希编码是使用二进制对标签编码做哈希映射。好处在于哈希编码器不需要维持类别字典，若后续出现训练集未出现的类别，哈希编码也能适用。但按位分开哈希编码，模型学习相对比较困难。

# !pip install category_encodersimport category_encoders as cex = pd.DataFrame({'gender':[2, 1, 1]})ce_encoder = ce.HashingEncoder(cols = ['gender']).fit(x)x_trans = ce_encoder.transform(x)
>>x_transcol_0  col_1  col_2  col_3  col_4  col_5  col_6  col_70      0      0      0      0      1      0      0      01      0      0      0      1      0      0      0      02      0      0      0      1      0      0      0      0

3. 独热编码（One-hot Encoder）

独热编码能很好解决标签编码对于回归任务中线性不可分的问题，它采用N位状态寄存器来对N个状态进行编码，简单来说就是利用0和1表示类别状态，它转换后的变量叫哑变量（dummy variables）。同样地，它处理不好高基数特征，基类越大会带来过很多列的稀疏特征，消耗内存和训练时间。

x = pd.DataFrame({'gender':['male', 'female', 'male']})x_dummies = pd.get_dummies(x['gender'])
>>>x_dummiesfemale  male0       0     11       1     02       0     1

4. 计数编码（Count Encoder）

计数编码也叫频次编码。就是用分类特征下不同类别的样本数去编码类别。清晰地反映了类别在数据集中的出现次数，缺点是忽略类别的物理意义，比如说两个类别出现频次相当，但是在业务意义上，模型的重要性也许不一样。

import category_encoders as cedf = pd.DataFrame({'cat_feat':['A', 'A', 'B', 'A', 'B', 'A']})count_encoder = ce.count.CountEncoder(cols = ['cat_feat']).fit(df)df_trans = count_encoder.transform(df)
>>df_transcat_feat0  41  42  23  44  25  4

5. 直方图编码（Bin Encoder）

直方图编码属于目标编码的一种，适用于分类任务。它先将类别属性分类，然后在对应属性下，统计不同类别标签的样本占比进行编码。直方图编码能清晰看出特征下不同类别对不同预测标签的贡献度[1]，缺点在于：使用了标签数据，若训练集和测试集的类别特征分布不一致，那么编码结果容易引发过拟合。此外，直方图编码出的特征数量是分类标签的类别数量，若标签类别很多，可能会给训练带来空间和时间上的负担。直方图编码样例如下图所示：

图1：直方图编码

import pandas as pd
class hist_encoder:    '''直方图编码器    @author: alvin ai    params:        df         (pd.DataFrame): 待编码的dataframe数据        encode_feat_name    (str): 编码的类别特征名，当前代码只支持单个特征编码，若要批量编码，请自行实现        label_name          (str): 类别标签    '''    def __init__(self, df, encode_feat_name, label_name):        self.df = df.copy()        self.encode_feat_name = encode_feat_name        self.label_name = label_name
    def fit(self):        '''用训练集获取编码字典'''        # 分子：类别特征下给定类别，在不同分类标签下各类别的数量        self.df['numerator'] = 1        numerator_df = self.df.groupby([self.encode_feat_name, self.label_name])['numerator'].count().reset_index()
        # 分母：分类标签下各类别的数量        self.df['denumerator'] = 1        denumerator_df = self.df.groupby(self.encode_feat_name)['denumerator'].count().reset_index()
        # 类别特征类别、分类标签类别：直方图编码映射字典        encoder_df = pd.merge(numerator_df, denumerator_df, on = self.encode_feat_name)        encoder_df['encode'] = encoder_df['numerator'] / encoder_df['denumerator'] 
        self.encoder_df = encoder_df[[self.encode_feat_name, self.label_name, 'encode']]
    def transform(self, test_df):        '''对测试集编码'''        # 依次编码出: hist特征1， hist特征2， ...        test_trans_df = test_df.copy()        for label_cat in test_trans_df[self.label_name].unique():            hist_feat = []            for cat_feat_val in test_trans_df[self.encode_feat_name].values:                try:                    encode_val = encoder_df[(encoder_df[self.label_name] == label_cat) & (encoder_df[self.encode_feat_name] == cat_feat_val)]['encode'].item()                    hist_feat.append(encode_val)                except:                    hist_feat.append(0)            encode_fname = self.encode_feat_name + '_en{}'.format(str(label_cat)) # 针对类别特征-类别label_cat的直方图编码特征名            test_trans_df[encode_fname] = hist_feat # 将编码的特征加入到原始数据中            return test_trans_df
# 初始化数据df = pd.DataFrame({'cat_feat':['A', 'A', 'B', 'A', 'B', 'A'], 'label':[0, 1, 0, 2, 1, 2]})encode_feat_name = 'cat_feat'label_name = 'label'
# 直方图编码he = hist_encoder(df, encode_feat_name, label_name)he.fit()df_trans = he.transform(df)
>>dfcat_feat  label0  A  01  A  12  B  03  A  24  B  15  A  2
>>df_transcat_feat  label  cat_feat_en0  cat_feat_en1  cat_feat_en20  A  0  0.25  0.25  0.51  A  1  0.25  0.25  0.52  B  0  0.50  0.50  0.03  A  2  0.25  0.25  0.54  B  1  0.50  0.50  0.05  A  2  0.25  0.25  0.5

6. WOE编码

WOE（Weight of Evidence，证据权重）编码适用于二分类任务，WOE表明自变量相对于因变量的预测能力。由于它是从信用评分世界演变而来的，它通常被描述为区分好客户和坏客户的衡量标准。“坏客户”是指拖欠贷款的客户。和“优质客户”指的是谁偿还贷款的客户。[8]

$WOE=\sum_{i}^{\#group} ln(\frac{p_{y_i}}{p_{n_i}})=\sum_{i}^{\#group}ln(\frac{\frac{\#y_i}{\#y_T}}{\frac{\#n_i}{\#n_T}})$ 其中，参数解释如下：

● $\#group$ ：分组的数量。

● $p_{y_i}$ ：组内违约用户数占比（即组内label=1的样本数占比）。

● $p_{n_i}$ ：组内正常用户数占比（即组内label=0的样本数占比）。

● $\frac{\#y_i}{\#y_T}$ ：组内违规用户数/所有违规用户数。

● $\frac{\#n_i}{\#n_T}$ ：组内正常用户数/所有正常用户数。

透过公式，我们可以把WOE理解成：每个分组内坏客户分布相对于优质客户分布之间的差异性。

据知乎主@马东什么[3]指出，WOE存在几个问题：

(1) 分母可能为0.

(2) 没有考虑不同类别数量的大小带来的影响，可能某类数量多，但最后计算出的WOE跟某样本数量少的类别的WOE一样。

(3) 只针对二分类问题。

(4) 训练集和测试集可能存在WOE编码差异（通病）。

对于问题1，源码[4]加入regularization（默认值为1）。

# Create a new column with regularized WOE.# Regularization helps to avoid division by zero.# Pre-calculate WOEs because logarithms are slow.nominator = (stats['sum'] + self.regularization) / (self._sum + 2*self.regularization)denominator = ((stats['count'] - stats['sum']) + self.regularization) / (self._count - self._sum + 2*self.regularization)woe = np.log(nominator / denominator)

对于问题2，可以考虑使用IV（Information Value），可以看作对WOE的加权，公式如下： $IV=\sum_{i}^{\#group}( p_{y_i}-p_{n_i})*ln(\frac{p_{y_i}}{p_{n_i}}))$ WOE和IV的区别和联系[2]是：

(1) WOE describes the relationship between a predictive variable and a binary target variable.

(2) IV measures the strength of that relationship.

扩展：IV常会被用来评估变量的预测能力，用于筛选变量：

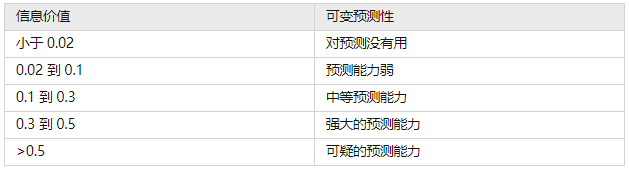
图2：不同IV值的预测性

对于问题3，可以考虑借鉴直方图编码的思路，将多分类标签，独热后依次进行WOE编码。[3]，而对于问题4，暂时无解。

from category_encoders import WOEEncoderimport pandas as pd
df = pd.DataFrame({'cat_feat':['A', 'A', 'B', 'A', 'B', 'A'], 'label':[0, 1, 0, 1, 1, 1]})enc = WOEEncoder(cols=['cat_feat']).fit(df, df['label'])df_trans = enc.transform(df)
>>df_transcat_feat  label0  0.287682  01  0.287682  12  -0.405465  03  0.287682  14  -0.405465  15  0.287682  1

7. 目标编码（Target Encoder）

2001年Micci等人提出的目标编码[5]，是一种有监督编码方法，适用于分类和回归任务中，高基类无序类别特征。

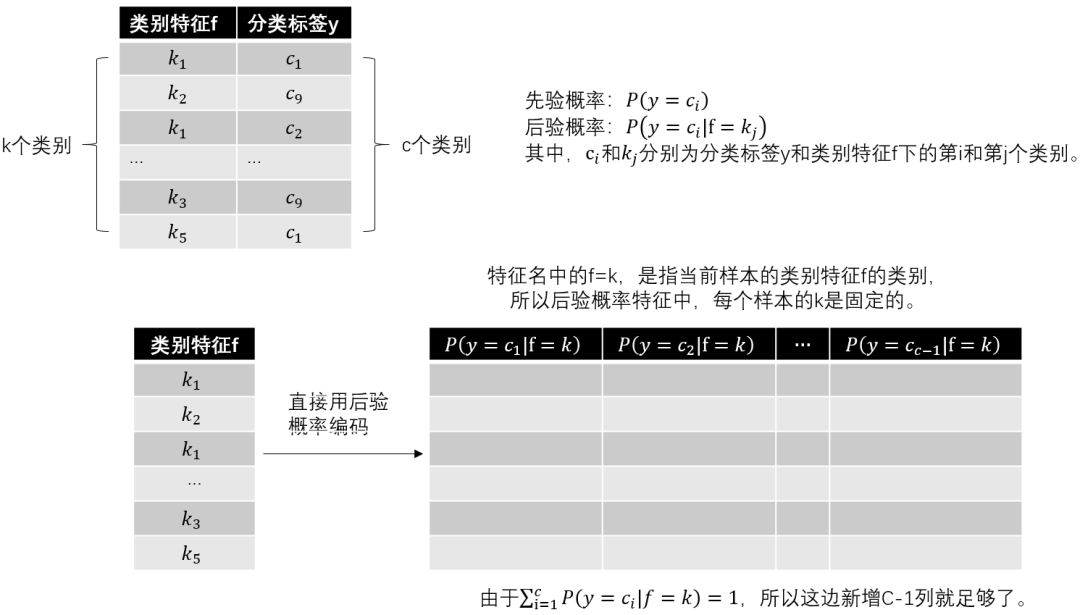
编码略显复杂，这里以分类任务为例，假设我们有类别型特征 $f$ ，分类标签 $y$ 。其中 $f$ 下有 $k$ 个类别， $y$ 有 $c$ 个类别。基于数据，我们可以计算出先验概率 $P(y=c_{i})$ 和后验概率 $P(y=c_{i}|f=k_{j})$ ， $c_i$ 和 $k_j$ 分别为分类标签 $y$ 和类别特征 $f$ 下的第 $i$ 和第 $j$ 个类别。这样我们能通过后验概率直接编码，如下图所示：

图3：后验概率编码

使用后验概率编码后新增的c-1列之间是线性相关的，会带来多重共线性问题。为此，目标编码结合了前验概率和后验概率去估算新的概率编码： $\hat{P}=\lambda * P(y=c_i)+(1-\lambda) *P(y=c_{i}|f=k)$ 对于回归问题，只需要将前面的概率换成均值即可，公式如下： $\hat{P}=\lambda * \frac{\sum y_{c_i}}{N} +(1-\lambda) * \frac{\sum y_{c_i}}{n_{f=k}}$ 从上面公式可知，如果测试集出现新的特征类别，那后验概率为0，只有先验概率，此时 $\lambda=1$ 。权重 $\lambda$ 的计算方式如下： $\lambda(n)=\frac{1}{1+e^{\frac{-(n-k)}{f}}}$

源码[6]如下：

# 默认参数：min_samples_leaf=1, smoothing=1.0smoove = 1 / (1 + np.exp(-(stats['count'] - self.min_samples_leaf) / self.smoothing))smoothing = prior * (1 - smoove) + stats['mean'] * smoovesmoothing[stats['count'] == 1] = prior

其中，默认值： $k=2$ 和 $f=1$ 。当 $n=k$ 时， $\lambda=0.5$ ，当 $n>k$ 时， $\lambda<0.5$ 。具体参数解释如下：

● $k$ ：min_samples_leaf，决定在cell内样本数至少为多少，我们才能完全相信它的估计。

● $n$ ：特征类别在训练集中的出现次数。因此当类别特征中某个类别出现次数越多，后验概率可信度越高，权重 $(1-\lambda)$ 会越大。

● $f$ ：控制了函数 $\lambda(n)$ 在拐点附近的斜率， $f$ 越大，坡度越缓。当 $k=1$ 时，不同 $f$ 值下的 $\lambda(n)$ 如下图所示。

图4：当k=1时，不同f值下的\lambda(n)

目标编码的好处是结合了先验概率和后验概率去编码，但由于概率是直接使用标签数据计算得到的，所以会引发过拟合问题。

from category_encoders import TargetEncoderimport pandas as pd
df = pd.DataFrame({'cat_feat':['A', 'A', 'B', 'A', 'B', 'A'], 'label':[0, 1, 0, 1, 1, 1]})enc = TargetEncoder(cols=['cat_feat']).fit(df, df['label'])df_trans = enc.transform(df)
>>df_transcat_feat  label0  0.746048      01  0.746048      12  0.544824      03  0.746048      14  0.544824      15  0.746048      1

8. 平均编码（Mean Encoder）

平均编码是基于目标编码的改进版。它的2点改动如下：

(1) 权重公式：其实没有本质上的区别，可自行修改函数内的参数。

'''param prior_weight_func:a function that takes in the number of observations,and outputs prior weight when a dict is passed,the default exponential decay function will be used:  k: the number of observations needed for the posterior to be weighted equally as the prior  f: larger f --> smaller slope'''self.prior_weight_func = eval('lambda x: 1 / (1 + np.exp((x - k) / f))', dict(prior_weight_func, np=np))

(2) 由于目标编码使用了标签，为了缓解编码带来模型过拟合问题，平均编码加入了K-fold编码思路，若分为5折，则用1-4折先fit后，再transform第5折，依次类推，将类别特征分5次编码出来。坏处是耗时。

# :param n_splits: the number of splits used in mean encoding. 默认n_splits=5for variable, target in product(self.categorical_features, self.target_values):    nf_name = '{}_pred_{}'.format(variable, target)     X_new.loc[:, nf_name] = np.nan    for large_ind, small_ind in skf.split(y, y):        nf_large, nf_small, prior, col_avg_y = MeanEncoder.mean_encode_subroutine(X_new.iloc[large_ind],y.iloc[large_ind],X_new.iloc[small_ind],variable, target, self.prior_weight_func)        X_new.iloc[small_ind, -1] = nf_small        self.learned_stats[nf_name].append((prior, col_avg_y))

代码过长，这里不予展示，详情请见[7]：

# 代码过长，这里不予展示，详情请见[7]class MeanEncoder...
df = pd.DataFrame({'cat_feat':['A', 'A', 'B', 'A', 'B', 'A', 'A', 'A', 'B', 'A', 'B', 'A', 'A', 'A', 'B', 'A', 'B', 'A'], 'label':[0, 1, 0, 2, 1, 2, 0, 1, 0, 2, 1, 2, 0, 1, 0, 2, 1, 2]})me = MeanEncoder(categorical_features = ['cat_feat'])x_trans = me.fit_transform(df, df['label'])
>>x_transcat_feat  label  cat_feat_pred_0  cat_feat_pred_1  cat_feat_pred_20  A  0  0.222280  0.222345  0.5553751  A  1  0.222280  0.222345  0.5553752  B  0  0.394580  0.588482  0.0169383  A  2  0.222280  0.222345  0.5553754  B  1  0.588482  0.394580  0.0169385  A  2  0.222345  0.222280  0.5553756  A  0  0.222345  0.222280  0.555375...

9. 模型编码（Model Encoder）

之前我写过文章【务实基础】CatBoost，里面有提到模型自带的类别特征编码。目前GBDT模型中，只有LGBM和CatBoost自带类别编码。LGBM的类别编码采用的是GS编码（Gradient Statistics），将类别特征转为累积值 $\frac{sum(gradient) }{sum(hessian)}$ (一阶偏导数之和/二阶偏导数之和)再进行直方图特征排序。使用起来也很简单，定义lgb数据集时，指定categorical_feature。

train_data = lgb.Dataset(data, label=label, feature_name=['c1', 'c2', 'c3'], categorical_feature=['c3'])

据官方文档介绍，GS编码比独热编码快大概8倍速度。而且文档里也建议，当类别变量为高基类时，哪怕是简单忽略类别含义或把它嵌入到低维数值空间里，只要将特征转为数值型，一般会表现的比较好。就个人使用来讲，我一般会对无序类别型变量进行模型编码，有序类别型变量直接按顺序标签编码即可。

虽然LGBM用GS编码类别特征看起来挺厉害的，但是存在两个问题：

● 计算时间长：因为每轮都要为每个类别值进行GS计算。

● 内存消耗大：对于每次分裂，都存储给定类别特征下，它不同样本划分到不同叶节点的索引信息。

所以CatBoost使用Ordered TS编码，既利用了TS省空间和速度的优势，也使用Ordered的方式缓解预测偏移问题。详情可见我历史文章。

图5：Ordered TS示意图

三、总结

我这里总结了以上类别编码方法的区别：

图6：类别特征编码总结

总结来说，关于类别特征，有以下心得：

(1) 统计类编码常常不适用于小样本，因为统计意义不明显。

(2) 当训练集和测试集分布不一致时，统计类编码往往会有预测偏移问题，所以一般会考虑结合交叉验证。

(3) 编码后特征数变多的编码方法，不适用于高基类的特征，会带来稀疏性和训练成本。

(4) 没有完美的编码方法，但感觉标签编码、平均编码、WOE编码和模型编码比较常用。

参考资料

[1] 特征工程之Histogram编码, 博文: https://blog.csdn.net/Chengliangyao/article/details/82623775

[2] 风控模型—WOE与IV指标的深入理解应用 - 求是汪在路上, 知乎: https://zhuanlan.zhihu.com/p/80134853

[3] 特征编码方法总结—part1 - 马东什么, 知乎: https://zhuanlan.zhihu.com/p/67475635

[4] woe.py, 源码: https://github.com/scikit-learn-contrib/category_encoders/blob/master/category_encoders/woe.py

[5] Micci-Barreca, D. (2001). A preprocessing scheme for high-cardinality categorical attributes in classification and prediction problems. *ACM SIGKDD Explorations Newsletter*, *3*(1), 27-32.

[6] target_encoder - category_encoders, 源码: http://contrib.scikit-learn.org/category_encoders/_modules/category_encoders/target_encoder.html#TargetEncoder

[7] 平均数编码：针对某个分类特征类别基数特别大的编码方式, 博文: https://www.cnblogs.com/wzdLY/p/9639519.html

[8] 证据权重 (WOE) 和信息价值 (IV) - python风控模型, 知乎: https://zhuanlan.zhihu.com/p/389734858