20分钟入门杨辉三角

freedom 摄影作品

今天准备做杨辉三角的题，老婆凑过来要跟我学写代码，看我盯着题目冥思苦想，就问我啥是杨辉三角? 那啥是杨辉三角？来，上题目！

题目描述

给定一个非负整数 numRows，生成「杨辉三角」的前 numRows 行。

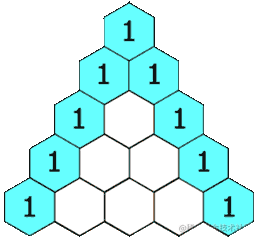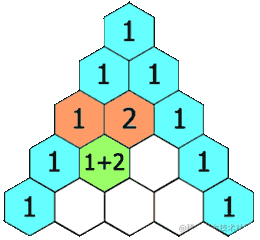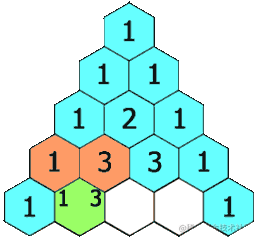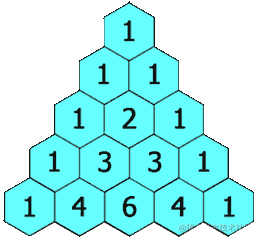
在「杨辉三角」中，每个数是它左上方和右上方的数的和。

示例 1:

输入: numRows = 5 输出: [[1],[1,1],[1,2,1],[1,3,3,1],[1,4,6,4,1]] 示例 2:

输入: numRows = 1 输出: [[1]]

提示:

1 <= numRows <= 30

题解

上面的动图生动形象地解释了杨辉三角的概念，这个三角形，顶部从1开始，下面每一行的每个数，都是它左上方和右上方的数的和。理解了概念之后，我们再从程序的角度来理解。如果把每一行的数据存入数组中，通过仔细观察，你会发现，这里面的每个数x(除了顶部的那个1)都等于这个数的上一行的两数之和。而这两个数的索引值，一个与x的索引相同，一个是x索引位的前一位索引。

是的，如果你熟悉动态规划，接下来动态方程就要出来了：dp[i][j] = dp[i-1][j] + dp[i-1][j-1]，杨辉三角也是一个比较典型的动态规划题目。接下来就是把思路如何实现的问题了。其实做动态规划题目，我有一个体会就是，先完成比较典型的问题，不要考虑边界，边界放到最后考虑，因为你很难一次性把所有细节考虑清楚。

首先，入参是行数，那就遍历这个行数，每次遍历得到当前行的所有数据。

// 定义返回结果
var res = [];
for(var i =0; i < numRows; i++){
    // 定义每行结果
    var dp = [];
    // todo
    // 获得每行的结果
    ...
    res.push(dp)
}
return res

上面把代码的大概逻辑写好了，相当于是一个模板。现在的关键问题就是如何得到每行的数据。

接下来，我现在需要在每行得到一个数组，这个数组作为元素添加到最终结果中。参考上面的dp动态方程dp[i][j] = dp[i-1][j] + dp[i-1][j-1]，遍历到当前第i行时，dp的元素就有i+1个(注意数学与程序索引的切换)，所以这里要遍历i+1次，根据这个动态方程来确定每个元素的值。

// 定义返回结果
var res = [];
for(var i =0; i < numRows; i++){
    // 定义每行结果
    var dp = [];
    // 获得每行的结果
    for(var j = 0;j<=i;j++){
       dp.push( res[i-1][j] +  res[i-1][j-1])
    }
    res.push(dp)
}
return res

这里面，还没有考虑到边界问题，即i=0及j=0的情况。这个问题很好解决，超边界之外的值，都取0就可以了。还有一个边界情况就是，第0行，直接得到结果添加进去就好了。所以最终完整代码如下：

/**
 * @param {number} numRows
 * @return {number[][]}
 */
var generate = function(numRows) {
    var res = []
    for(var i = 0; i< numRows; i++){
        var dp = []
        if(i=== 0) {
            dp = [1]
            res.push(dp)
        } else {
            for(var j = 0;j<=i;j++){
                dp.push((j === res[i-1].length ? 0: res[i-1][j]) + (j-1 <0? 0 : res[i-1][j-1]))
            }
            res.push(dp)
        }
    }
    return res
};

我看了官方题解，其实思路一样的，我第一次接触杨辉三角就能解出来，算不错了，写下心路历程，继续进步！

复杂度分析

• 时间复杂度：O(numRows²)，比较好理解，最外层循环numRows次，里面累计是(1+n)*n/2，所以复杂度可以理解为n²
• 空间复杂度：O(1)，常量级的空间占用

题目链接：https://leetcode-cn.com/problems/pascals-triangle