本福特定律和统计中的造假检测
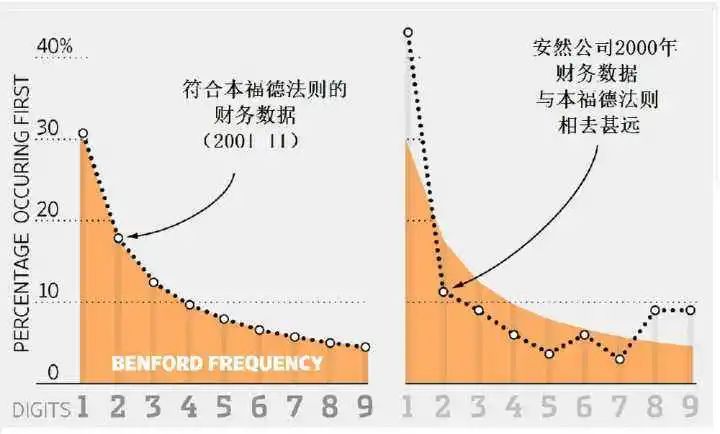
英文原文:https://www.statisticalconsultants.co.nz/blog/benfords-law-and-accounting-fraud-detection.html
一、基本概念
15435 首位是 156 首位是 59001 首位是 9199 首位是 19 首位是 9
二、数位分布概率 第1位数字
出现概率
1
0.301
2
0.176
3
0.125
4
0.097
5
0.079
6
0.067
7
0.058
8
0.051
9
0.046
第1位数字 | 出现概率 |
1 | 0.301 |
2 | 0.176 |
3 | 0.125 |
4 | 0.097 |
5 | 0.079 |
6 | 0.067 |
7 | 0.058 |
8 | 0.051 |
9 | 0.046 |
三、本福特分布图
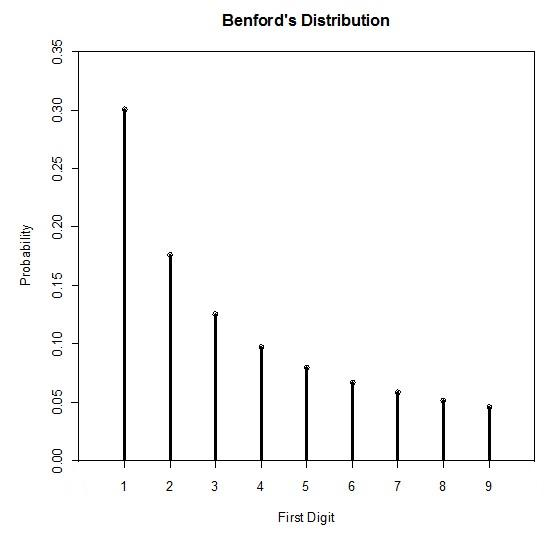
四、本福特分布公式
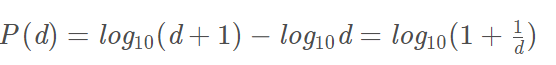
六、本福特定律适用于哪类数据?
具有通过来自多个分布的数字的数学组合形成的值的数据。 具有多种数字的数据,例如 具有数百,数千,数万等数值的数据。 数据集相当大。 数据是右倾斜的,即平均值大于中值,并且分布具有长的右尾而不是对称的。 数据没有预定义的最大值或最小值(最小值为零)。
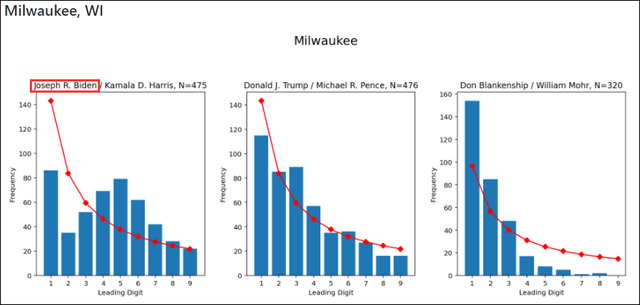
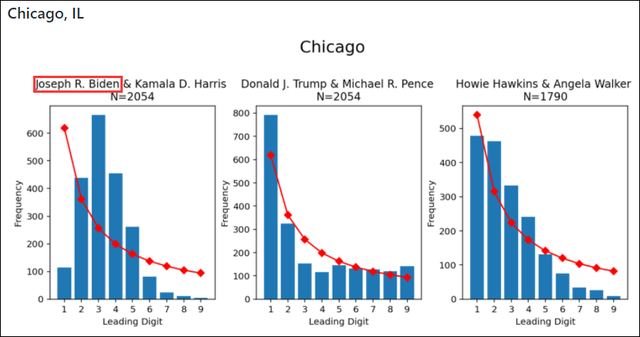
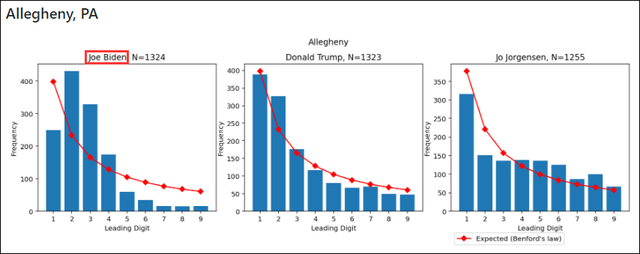
七、会计欺诈检测与取证分析
1)大型企业的应付账款数据
2)本福特的分析应用于组织的费用数据
八、广义本福特的分布表
数位 | 第1位 | 第2位 | 第3位 | 第4位 | 第5位 |
0 | NA | 0.11968 | 0.10178 | 0.10018 | 0.10002 |
1 | 0.30103 | 0.11389 | 0.10138 | 0.10014 | 0.10001 |
2 | 0.17609 | 0.10882 | 0.10097 | 0.1001 | 0.10001 |
3 | 0.12494 | 0.10433 | 0.10057 | 0.10006 | 0.10001 |
4 | 0.09691 | 0.10031 | 0.10018 | 0.10002 | 0.1 |
5 | 0.07918 | 0.09668 | 0.09979 | 0.09998 | 0.1 |
6 | 0.06695 | 0.09337 | 0.0994 | 0.09994 | 0.09999 |
7 | 0.05799 | 0.09035 | 0.09902 | 0.0999 | 0.09999 |
8 | 0.05115 | 0.08757 | 0.09864 | 0.09986 | 0.09999 |
9 | 0.04576 | 0.085 | 0.09827 | 0.09982 | 0.09998 |
九、一般分布公式
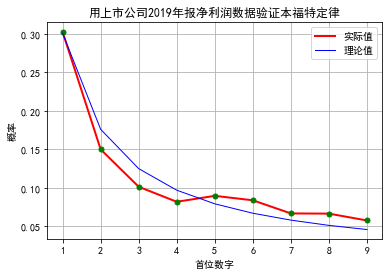
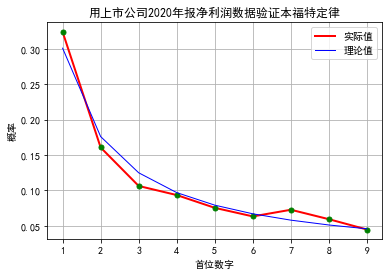
十、上市公司年报净利润数据验证本福特定律
# 验证本福特定律import tushare as ts # 股票数据获取的一个包import mathimport matplotlib.pyplot as pltimport pandas as pdfrom functools import reducefrom pylab import *# 这一句让pyplot支持中文显示mpl.rcParams['font.sans-serif'] = ['SimHei']# 获取首位的函数def firstDigital(x):x= round(x)while x >= 10:x //= 10return x# 首位概率累加def addDigit(lst, digit):lst[digit-1]+=1return lst# 理论值:每位概率理论值用于对比th_freq=[math.log((x+1)/x, 10) for x in range(1,10)]#分别获得2019,2020年报数据df= ts.get_report_data(2019, 4)# 只取净利润>0的数据,首先进行次数统计freq= reduce(addDigit, map(firstDigital, filter(lambda x:x>0, df['net_profits'])), [0]*9)# 再计算实际概率pr_freq= [x/sum(freq) for x in freq]print(th_freq)print(pr_freq)# 作图plt.title('用上市公司2019年报净利润数据验证本福特定律')plt.xlabel("首位数字")plt.ylabel("概率")plt.xticks(range(9), range(1,10))plt.plot(pr_freq,"r-",linewidth=2, label= '实际值')plt.plot(pr_freq, "go", markersize=5)plt.plot(th_freq,"b-",linewidth=1, label= '理论值')plt.grid(True)plt.legend()plt.show()

长按关注公众号 长按加作者好友
评论
