一次搞定九大排序策略
共 37542字,需浏览 76分钟
·
2021-08-13 16:13
点击上方 三分钟学前端,关注公众号
回复交流,加入前端编程面试算法每日一题群
14.1 冒泡排序
原理:
从左到右,相邻元素进行比较,如果前一个元素值大于后一个元素值(正序),则交换,这样一轮下来,将最大的数在最右边冒泡出来。这样一轮一轮下来,最后实现从小到大排序。
动图演示:
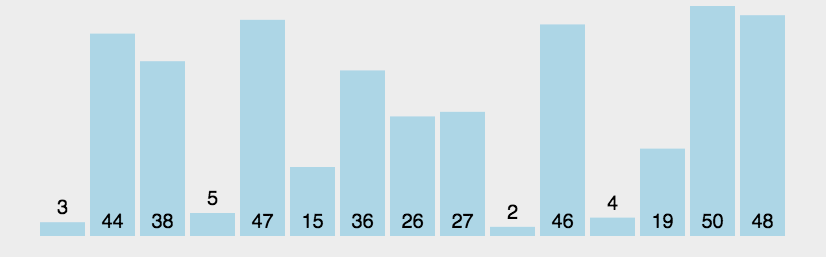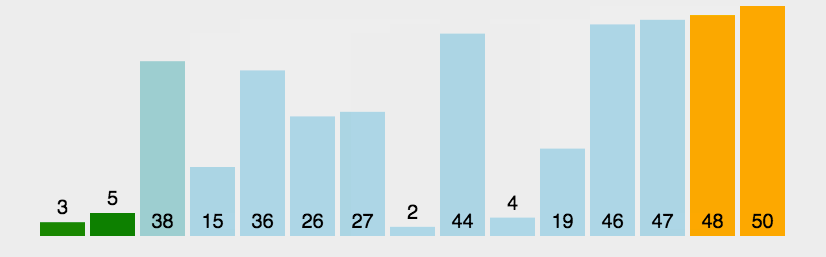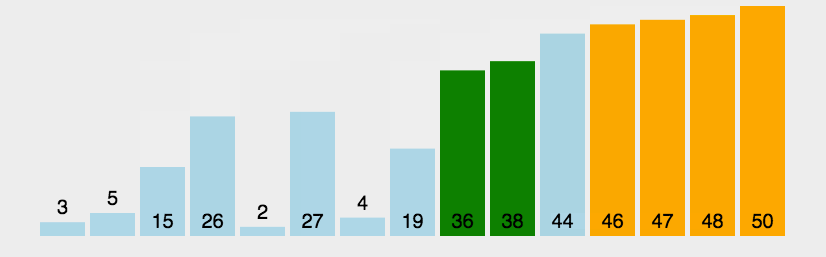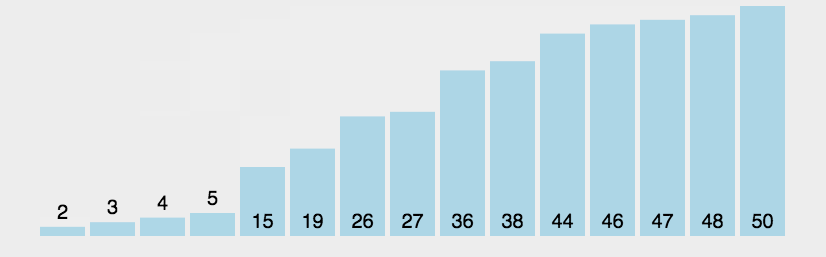
代码实现:
function bubbleSort(arr) {
for (let i = 0; i < arr.length; i++) {
for (let j = 0; j < arr.length - i - 1; j++) {
if (arr[j] > arr[j + 1]) {
const temp = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = temp;
}
}
}
}
// 改进冒泡排序
function bubbleSort1(arr) {
for (let i = 0; i < arr.length; i++) {
// 提前退出冒泡循环的标识位
let flag = false;
for (let j = 0; j < arr.length - i - 1; j++) {
if (arr[j] > arr[j + 1]) {
const temp = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = temp;
flag = true;
// 表示发生了数据交换
}
}
// 没有数据交换
if(!flag) break
}
}
// 测试
let arr = [1, 3, 2, 5, 4]
bubbleSort(arr)
console.log(arr) // [1, 2, 3, 4, 5]
let arr1 = [1, 3, 2, 5, 4]
bubbleSort1(arr1)
console.log(arr1) // [1, 2, 3, 4, 5]
复杂度分析:
时间复杂度:最好时间复杂度 O(n),平均时间复杂度 O(n^2^) 空间复杂度:O(1)
14.2 选择排序
原理
从未排序的序列中找到最大(或最小的)放在已排序序列的末尾(为空则放在起始位置),重复该操作,知道所有数据都已放入已排序序列中。
动态演示
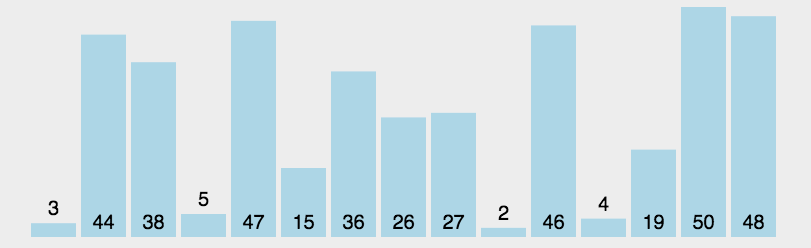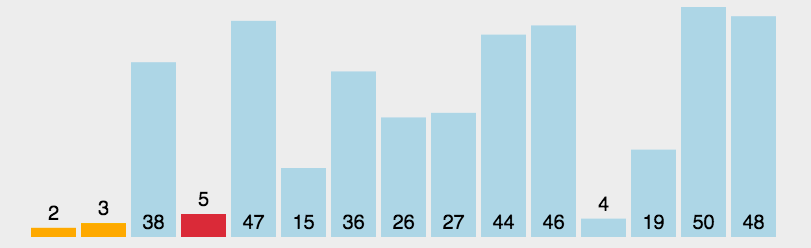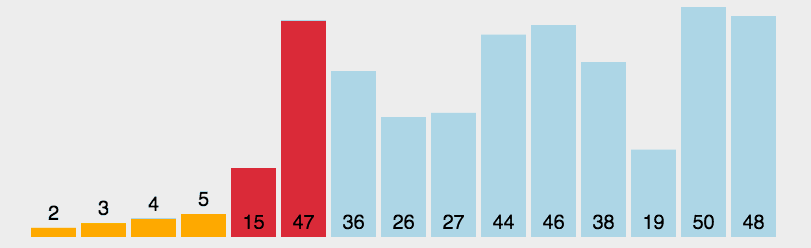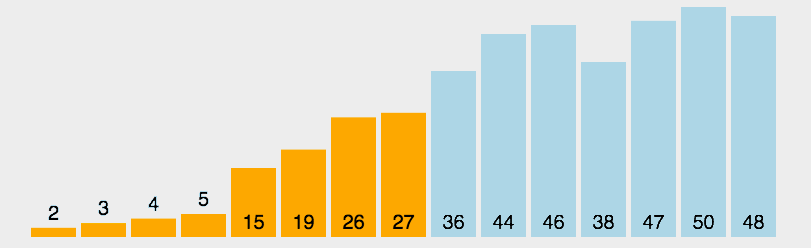
代码实现
function selectionSort(arr) {
let length = arr.length,
indexMin
for(let i = 0; i < length - 1; i++) {
indexMin = i
for(let j = i; j < length; j++) {
if(arr[indexMin] > arr[j]) {
indexMin = j
}
}
if(i !== indexMin) {
let temp = arr[i]
arr[i] = arr[indexMin]
arr[indexMin] = temp
}
}
}
// 测试
let arr = [1, 3, 2, 5, 4]
selectionSort(arr)
console.log(arr) // [1, 2, 3, 4, 5]
复杂度分析
**时间复杂度:**O(n^2^)
**空间复杂度:**O(1)
14.3 归并排序
原理
它采用了分治策略,将数组分成2个较小的数组,然后每个数组再分成两个更小的数组,直至每个数组里只包含一个元素,然后将小数组不断的合并成较大的数组,直至只剩下一个数组,就是排序完成后的数组序列。
实现步骤:
将原始序列平分成两个小数组 判断小数组长度是否为1,不为1则继续分裂 原始数组被分称了长度为1的多个小数组,然后合并相邻小数组(有序合并) 不断合并小数组,直到合并称一个数组,则为排序后的数组序列
动图演示
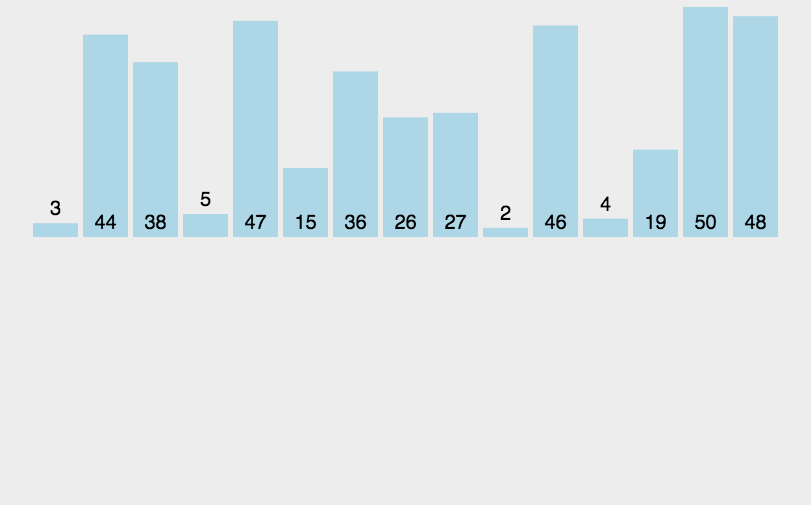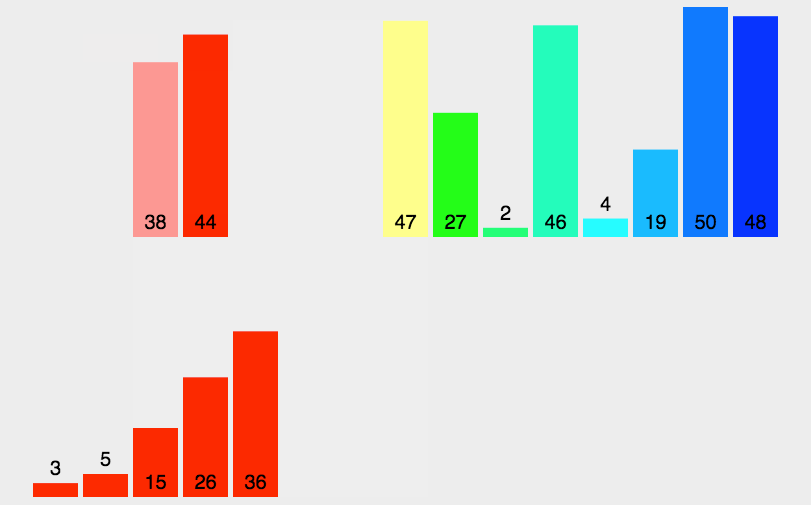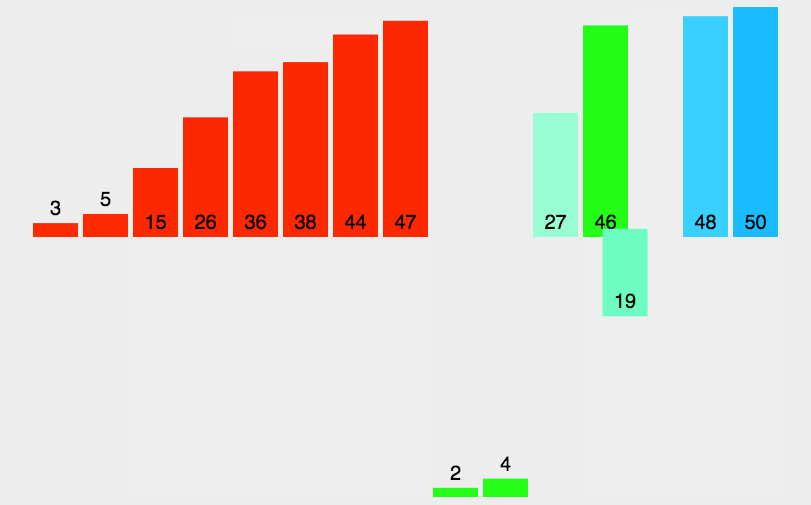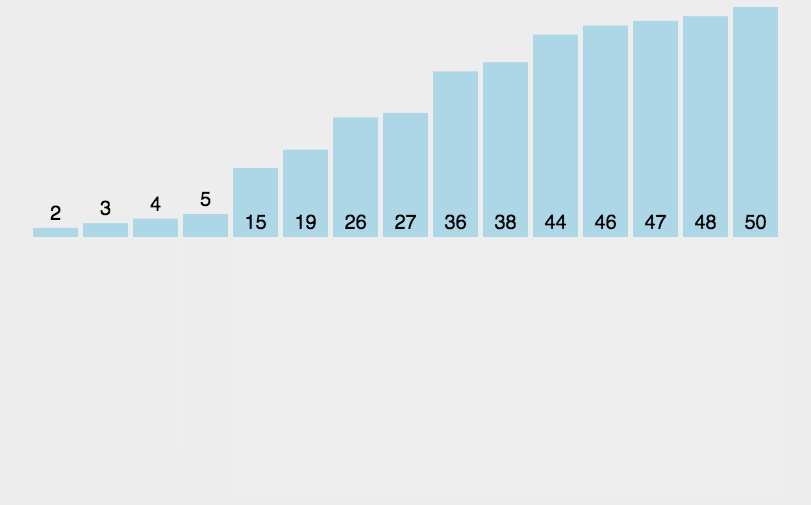
代码实现
function mergeSort(arr) {
let array = mergeSortRec(arr)
return array
}
// 若分裂后的两个数组长度不为 1,则继续分裂
// 直到分裂后的数组长度都为 1,
// 然后合并小数组
function mergeSortRec(arr) {
let length = arr.length
if(length === 1) {
return arr
}
let mid = Math.floor(length / 2),
left = arr.slice(0, mid),
right = arr.slice(mid, length)
return merge(mergeSortRec(left), mergeSortRec(right))
}
// 顺序合并两个小数组left、right 到 result
function merge(left, right) {
let result = [],
ileft = 0,
iright = 0
while(ileft < left.length && iright < right.length) {
if(left[ileft] < right[iright]){
result.push(left[ileft ++])
} else {
result.push(right[iright ++])
}
}
while(ileft < left.length) {
result.push(left[ileft ++])
}
while(iright < right.length) {
result.push(right[iright ++])
}
return result
}
// 测试
let arr = [1, 3, 2, 5, 4]
console.log(mergeSort(arr)) // [1, 2, 3, 4, 5]
复杂度分析
**时间复杂度:**O(nlog~2~n)
**空间复杂度:**O(n)
14.4 快速排序
原理
和归并排序一致,它也使用了分治策略的思想,它也将数组分成一个个小数组,但与归并不同的是,它实际上并没有将它们分隔开。
快排使用了分治策略的思想,所谓分治,顾名思义,就是分而治之,将一个复杂的问题,分成两个或多个相似的子问题,在把子问题分成更小的子问题,直到更小的子问题可以简单求解,求解子问题,则原问题的解则为子问题解的合并。
快排的过程简单的说只有三步:
首先从序列中选取一个数作为基准数 将比这个数大的数全部放到它的右边,把小于或者等于它的数全部放到它的左边 (一次快排 partition)然后分别对基准的左右两边重复以上的操作,直到数组完全排序
具体按以下步骤实现:
1,创建两个指针分别指向数组的最左端以及最右端 2,在数组中任意取出一个元素作为基准 3,左指针开始向右移动,遇到比基准大的停止 4,右指针开始向左移动,遇到比基准小的元素停止,交换左右指针所指向的元素 5,重复3,4,直到左指针超过右指针,此时,比基准小的值就都会放在基准的左边,比基准大的值会出现在基准的右边 6,然后分别对基准的左右两边重复以上的操作,直到数组完全排序
注意这里的基准该如何选择喃?最简单的一种做法是每次都是选择最左边的元素作为基准:
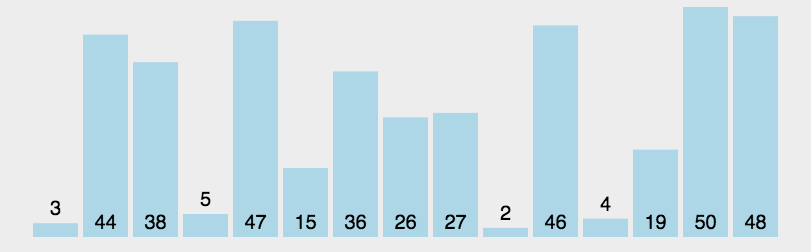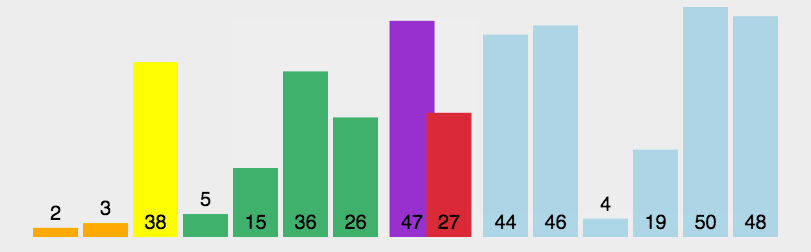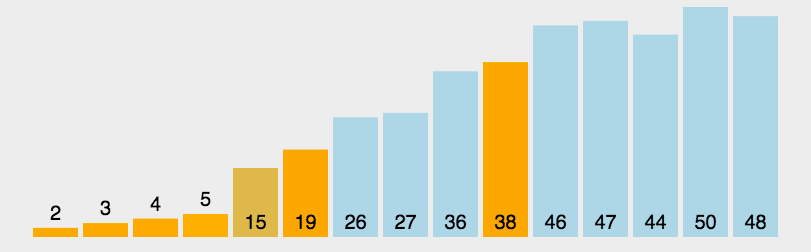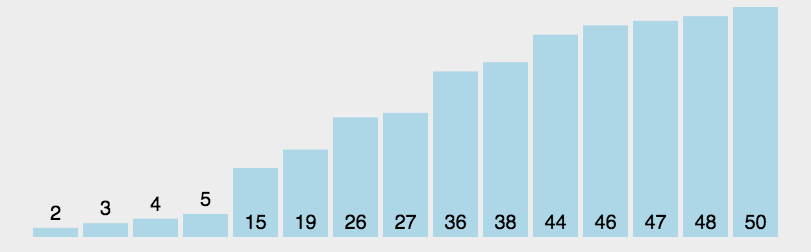
但这对几乎已经有序的序列来说,并不是最好的选择,它将会导致算法的最坏表现。还有一种做法,就是选择中间的数或通过 Math.random() 来随机选取一个数作为基准,下面的代码实现就是以随机数作为基准。
代码实现
let quickSort = (arr) => {
quick(arr, 0 , arr.length - 1)
}
let quick = (arr, left, right) => {
let index
if(left < right) {
// 划分数组
index = partition(arr, left, right)
if(left < index - 1) {
quick(arr, left, index - 1)
}
if(index < right) {
quick(arr, index, right)
}
}
}
// 一次快排
let partition = (arr, left, right) => {
// 取中间项为基准
var datum = arr[Math.floor(Math.random() * (right - left + 1)) + left],
i = left,
j = right
// 开始调整
while(i <= j) {
// 左指针右移
while(arr[i] < datum) {
i++
}
// 右指针左移
while(arr[j] > datum) {
j--
}
// 交换
if(i <= j) {
swap(arr, i, j)
i += 1
j -= 1
}
}
return i
}
// 交换
let swap = (arr, i , j) => {
let temp = arr[i]
arr[i] = arr[j]
arr[j] = temp
}
// 测试
let arr = [1, 3, 2, 5, 4]
quickSort(arr)
console.log(arr) // [1, 2, 3, 4, 5]
// 第 2 个最大值
console.log(arr[arr.length - 2]) // 4
快排是从小到大排序,所以第 k 个最大值在 n-k 位置上
复杂度分析
时间复杂度:O(nlog~2~n) 空间复杂度:O(nlog~2~n)
14.5 希尔排序
1959年Shell发明,第一个突破 O(n^2^) 的排序算法,是简单插入排序的改进版。它与插入排序的不同之处在于,它会优先比较距离较远的元素。
插入排序
插入排序的工作原理是通过构建有序序列,对于未排序数据,在已排序序列中从后向前扫描,找到相应位置并插入
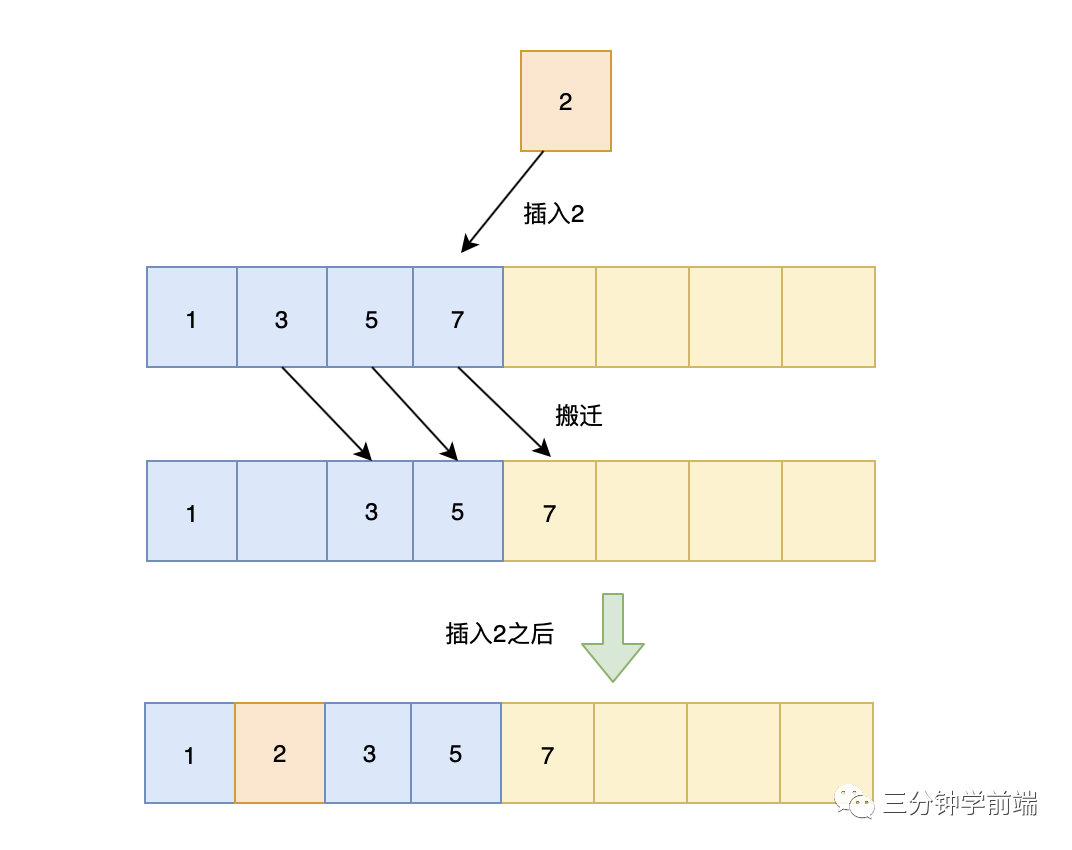
代码实现:
function insertionSort(arr) {
let n = arr.length;
let preIndex, current;
for (let i = 1; i < n; i++) {
preIndex = i - 1;
current = arr[i];
while (preIndex >= 0 && arr[preIndex] > current) {
arr[preIndex + 1] = arr[preIndex];
preIndex--;
}
arr[preIndex + 1] = current;
}
return arr;
}
插入算法的核心思想是取未排序区间中的元素,在已排序区间中找到合适的插入位置将其插入,并保证已排序区间数据一直有序。重复这个过程,直到未排序区间中元素为空,算法结束。
复杂度分析:
时间复杂度:O(n^2^) 空间复杂度:O(1)
希尔排序
回顾一下上面的插入排序:
第一趟插入排序后,我们得到的有效序列长度为 2第二趟插入排序后,我们得到的有效序列长度为 3... 直到这个序列有序
所以,如果序列足够乱的话,时间复杂度为 O(n^2^)
希尔排序又是如何优化的喃?
希尔排序又叫缩小增量排序,就是把数列进行分组(组内不停使用插入排序),直至从宏观上看起来有序,最后插入排序起来就容易了(无须多次移位或交换)。
其中组的数量称为 增量 ,显然的是,增量是不断递减的(直到增量为1)
那我们有是如何进行分组喃?
**往往的:**如果一个数列有 8 个元素,我们第一趟的增量是 4 ,第二趟的增量是 2 ,第三趟的增量是 1 。如果一个数列有 18 个元素,我们第一趟的增量是 9 ,第二趟的增量是 4 ,第三趟的增量是2 ,第四趟的增量是 1
很明显我们可以用一个序列来表示增量:n/2、(n/2)/2、...、1,每次增量都/2
例如:
let arr = [4, 1, 5, 8, 7, 3]
排序前:
将该数组看成三组( Math.floor(arr.length/2)),分别是:[4, 1],[5, 8],[7, 3]
第一趟排序:
对三组数据分别进行插入排序,因此我们三个数组得到的结果为: [1, 4],[5, 8],[3, 7]
此时数组是这样子的:[1, 4, 5, 8, 3, 7]
第二趟排序:
增量减少了,上面增量是 3,此时增量应该为1了,因此把[1, 4, 5, 8, 3, 7]看成一个数组(从宏观上是有序的了),对其进行插入排序,直至有序
代码实现:
function shellSort(arr) {
let n = arr.length;
for (let gap = Math.floor(n / 2); gap > 0; gap = Math.floor(gap / 2)) {
for (let i = gap; i < n; i++) {
let j = i;
let current = arr[i];
while (j - gap >= 0 && current < arr[j - gap]) {
arr[j] = arr[j - gap];
j = j - gap;
}
arr[j] = current;
}
}
return arr;
}
复杂度分析:
时间复杂度:O(nlogn) 空间复杂度:O(1)
14.6 计数排序
原理
计数排序不是基于比较的排序算法,其核心在于将输入的数据值转化为键存储在额外开辟的数组空间中。
作为一种线性时间复杂度的排序,计数排序要求输入的数据必须是有确定范围的整数。它是一种典型的拿空间换时间的排序算法
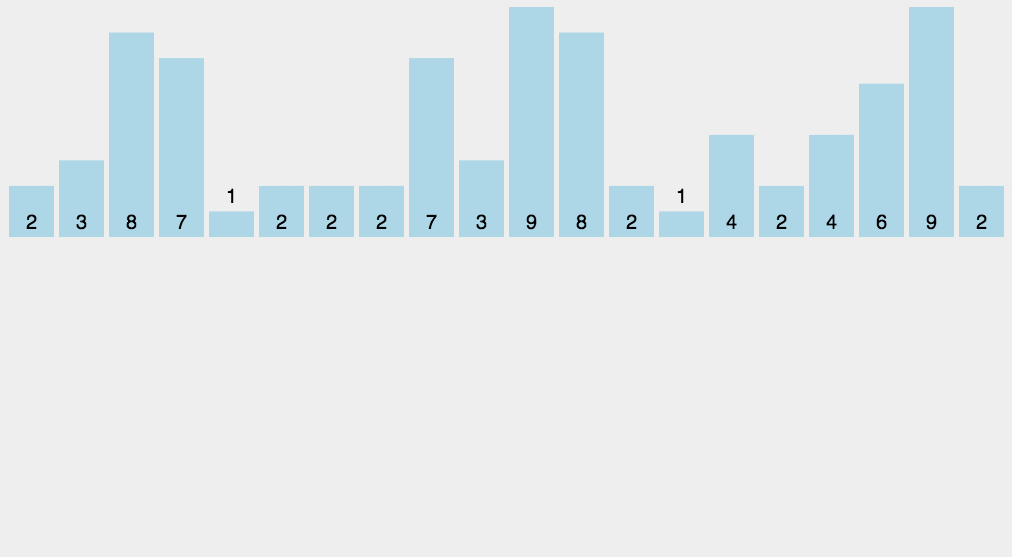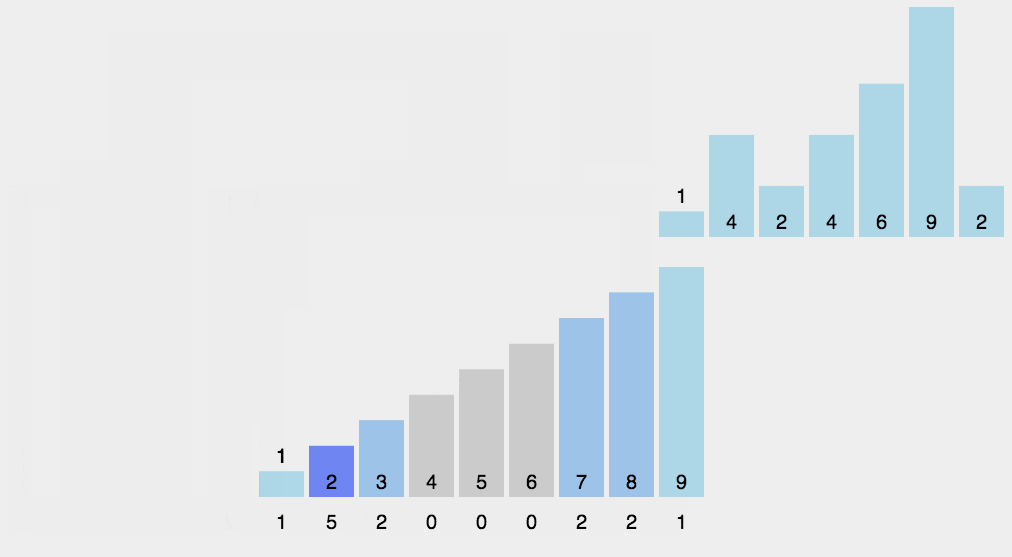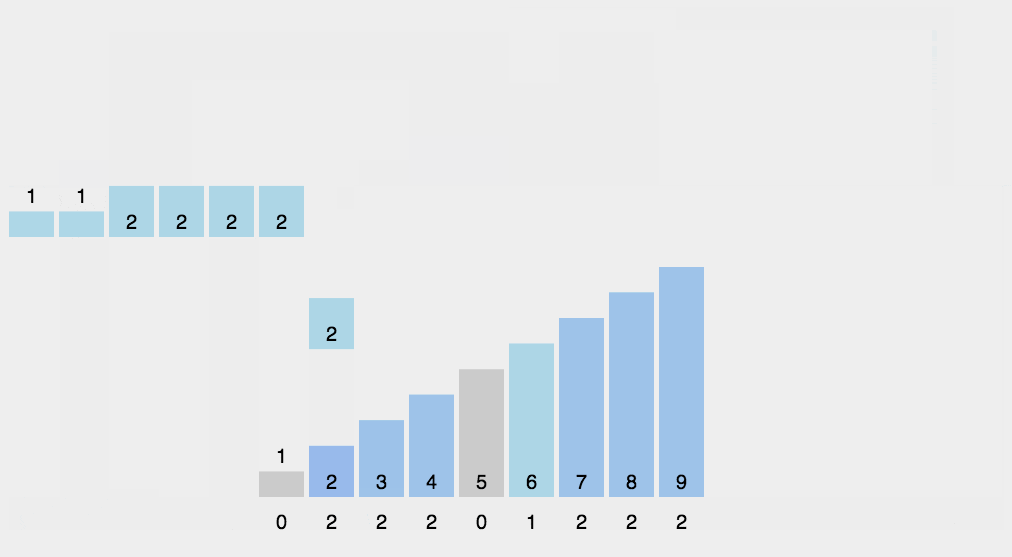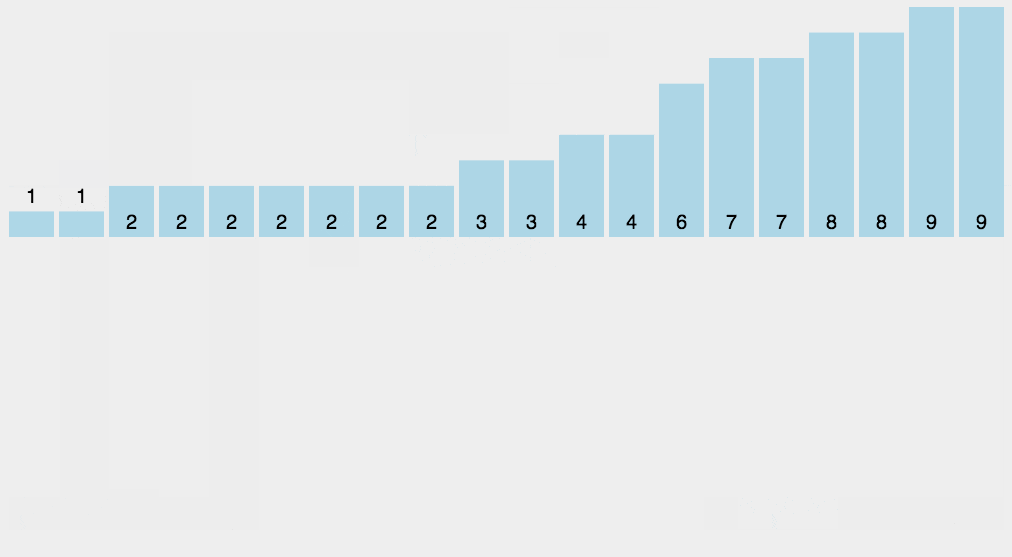
代码实现
function countingSort(arr, maxValue) => {
// 开辟的新的数组,用于将输入的数据值转化为键存储
var bucket = new Array(maxValue + 1),
sortedIndex = 0,
arrLen = arr.length,
bucketLen = maxValue + 1
// 存储
for (var i = 0; i < arrLen; i++) {
if (!bucket[arr[i]]) {
bucket[arr[i]] = 0
}
bucket[arr[i]]++
}
// 将数据从bucket按顺序写入arr中
for (var j = 0; j < bucketLen; j++) {
while(bucket[j]-- > 0) {
arr[sortedIndex++] = j
}
}
return arr
}
复杂度分析
时间复杂度:O(n+k) 空间复杂度:O(n+k)
14.7 桶排序
原理
桶排序是计数排序的升级版。它也是利用函数的映射关系。
桶排序 (Bucket sort)的工作的原理:假设输入数据服从均匀分布,将数据分到有限数量的桶里,每个桶再分别排序(有可能再使用别的排序算法或是以递归方式继续使用桶排序进行排)。
完整步骤:
首先使用 arr 来存储频率 然后创建一个数组(有数量的桶),将频率作为数组下标,对于出现频率不同的数字集合,存入对应的数组下标(桶内)即可。
// 桶排序
let bucketSort = (arr) => {
let bucket = [], res = []
arr.forEach((value, key) => {
// 利用映射关系(出现频率作为下标)将数据分配到各个桶中
if(!bucket[value]) {
bucket[value] = [key]
} else {
bucket[value].push(key)
}
})
// 遍历获取出现频率
for(let i = 0;i <= bucket.length - 1;i++){
if(bucket[i]) {
res.push(...bucket[i])
}
}
return res
}
复杂度分析:
时间复杂度:O(n) 空间复杂度:O(n)
14.8 基数排序
原理
基数排序是一种非比较型整数排序算法,其原理是将整数按位数切割成不同的数字,然后按每个位数分别比较。由于整数也可以表达字符串(比如名字或日期)和特定格式的浮点数,所以基数排序也不是只能使用于整数。
完整步骤:
取得数组中的最大数,并取得位数; arr为原始数组,从最低位开始取每个位组成radix数组; 对radix进行计数排序(利用计数排序适用于小范围数的特点);
动图演示

代码实现
//LSD Radix Sort
var counter = [];
function radixSort(arr, maxDigit) {
var mod = 10;
var dev = 1;
for (var i = 0; i < maxDigit; i++, dev *= 10, mod *= 10) {
for(var j = 0; j < arr.length; j++) {
var bucket = parseInt((arr[j] % mod) / dev);
if(counter[bucket]==null) {
counter[bucket] = [];
}
counter[bucket].push(arr[j]);
}
var pos = 0;
for(var j = 0; j < counter.length; j++) {
var value = null;
if(counter[j]!=null) {
while ((value = counter[j].shift()) != null) {
arr[pos++] = value;
}
}
}
}
return arr;
}
复杂度分析
时间复杂度:基数排序基于分别排序,分别收集,所以是稳定的。但基数排序的性能比桶排序要略差,每一次关键字的桶分配都需要O(n)的时间复杂度,而且分配之后得到新的关键字序列又需要O(n)的时间复杂度。假如待排数据可以分为d个关键字,则基数排序的时间复杂度将是O(d*2n) ,当然d要远远小于n,因此基本上还是线性级别的 空间复杂度:O(n+k),其中k为桶的数量。一般来说n>>k,因此额外空间需要大概n个左右
基数排序 vs 计数排序 vs 桶排序
这三种排序算法都利用了桶的概念,但对桶的使用方法上有明显差异:
基数排序:根据键值的每位数字来分配桶; 计数排序:每个桶只存储单一键值; 桶排序:每个桶存储一定范围的数值;
14.9 堆排序
原理
堆是一棵完全二叉树,它可以使用数组存储,并且大顶堆的最大值存储在根节点(i=1),所以我们可以每次取大顶堆的根结点与堆的最后一个节点交换,此时最大值放入了有效序列的最后一位,并且有效序列减1,有效堆依然保持完全二叉树的结构,然后堆化,成为新的大顶堆,重复此操作,知道有效堆的长度为 0,排序完成。
完整步骤为:
将原序列(n个)转化成一个大顶堆 设置堆的有效序列长度为 n 将堆顶元素(第一个有效序列)与最后一个子元素(最后一个有效序列)交换,并有效序列长度减1 堆化有效序列,使有效序列重新称为一个大顶堆 重复以上2步,直到有效序列的长度为 1,排序完成
动图演示

代码实现
function heapSort(items) {
// 构建大顶堆
buildHeap(items, items.length-1)
// 设置堆的初始有效序列长度为 items.length - 1
let heapSize = items.length - 1
for (var i = items.length - 1; i > 1; i--) {
// 交换堆顶元素与最后一个有效子元素
swap(items, 1, i);
// 有效序列长度减 1
heapSize --;
// 堆化有效序列(有效序列长度为 currentHeapSize,抛除了最后一个元素)
heapify(items, heapSize, 1);
}
return items;
}
// 原地建堆
// items: 原始序列
// heapSize: 有效序列长度
function buildHeap(items, heapSize) {
// 从最后一个非叶子节点开始,自上而下式堆化
for (let i = Math.floor(heapSize/2); i >= 1; --i) {
heapify(items, heapSize, i);
}
}
function heapify(items, heapSize, i) {
// 自上而下式堆化
while (true) {
var maxIndex = i;
if(2*i <= heapSize && items[i] < items[i*2] ) {
maxIndex = i*2;
}
if(2*i+1 <= heapSize && items[maxIndex] < items[i*2+1] ) {
maxIndex = i*2+1;
}
if (maxIndex === i) break;
swap(items, i, maxIndex); // 交换
i = maxIndex;
}
}
function swap(items, i, j) {
let temp = items[i]
items[i] = items[j]
items[j] = temp
}
// 测试
var items = [,1, 9, 2, 8, 3, 7, 4, 6, 5]
heapSort(items)
// [empty, 1, 2, 3, 4, 5, 6, 7, 8, 9]
测试成功
复杂度分析
**时间复杂度:**建堆过程的时间复杂度是 O(n),排序过程的时间复杂度是O(nlogn),整体时间复杂度是O(nlogn)空间复杂度: O(1)
14.10 加深
14.10.1 介绍一下快排原理以及时间复杂度,并实现一个快排
快排使用了分治策略的思想,所谓分治,顾名思义,就是分而治之,将一个复杂的问题,分成两个或多个相似的子问题,在把子问题分成更小的子问题,直到更小的子问题可以简单求解,求解子问题,则原问题的解则为子问题解的合并。
快排的过程简单的说只有三步:
首先从序列中选取一个数作为基准数 将比这个数大的数全部放到它的右边,把小于或者等于它的数全部放到它的左边 (一次快排 partition)然后分别对基准的左右两边重复以上的操作,直到数组完全排序
具体按以下步骤实现:
1,创建两个指针分别指向数组的最左端以及最右端 2,在数组中任意取出一个元素作为基准 3,左指针开始向右移动,遇到比基准大的停止 4,右指针开始向左移动,遇到比基准小的元素停止,交换左右指针所指向的元素 5,重复3,4,直到左指针超过右指针,此时,比基准小的值就都会放在基准的左边,比基准大的值会出现在基准的右边 6,然后分别对基准的左右两边重复以上的操作,直到数组完全排序
注意这里的基准该如何选择喃?最简单的一种做法是每次都是选择最左边的元素作为基准:

但这对几乎已经有序的序列来说,并不是最好的选择,它将会导致算法的最坏表现。还有一种做法,就是选择中间的数或通过 Math.random() 来随机选取一个数作为基准,下面的代码实现就是以随机数作为基准。
代码实现
let quickSort = (arr) => {
quick(arr, 0 , arr.length - 1)
}
let quick = (arr, left, right) => {
let index
if(left < right) {
// 划分数组
index = partition(arr, left, right)
if(left < index - 1) {
quick(arr, left, index - 1)
}
if(index < right) {
quick(arr, index, right)
}
}
}
// 一次快排
let partition = (arr, left, right) => {
// 取中间项为基准
var datum = arr[Math.floor(Math.random() * (right - left + 1)) + left],
i = left,
j = right
// 开始调整
while(i <= j) {
// 左指针右移
while(arr[i] < datum) {
i++
}
// 右指针左移
while(arr[j] > datum) {
j--
}
// 交换
if(i <= j) {
swap(arr, i, j)
i += 1
j -= 1
}
}
return i
}
// 交换
let swap = (arr, i , j) => {
let temp = arr[i]
arr[i] = arr[j]
arr[j] = temp
}
// 测试
let arr = [1, 3, 2, 5, 4]
quickSort(arr)
console.log(arr) // [1, 2, 3, 4, 5]
// 第 2 个最大值
console.log(arr[arr.length - 2]) // 4
快排是从小到大排序,所以第 k 个最大值在 n-k 位置上
复杂度分析
时间复杂度:O(nlogn) 空间复杂度:O(nlogn)
更多解答
14.10.2 打乱数组(洗牌算法)
打乱一个没有重复元素的数组。
示例:
// 以数字集合 1, 2 和 3 初始化数组。
int[] nums = {1,2,3};
Solution solution = new Solution(nums);
// 打乱数组 [1,2,3] 并返回结果。任何 [1,2,3]的排列返回的概率应该相同。
solution.shuffle();
// 重设数组到它的初始状态[1,2,3]。
solution.reset();
// 随机返回数组[1,2,3]打乱后的结果。
solution.shuffle();
解答:Fisher-Yates 洗牌算法
let Solution = function(nums) {
this.nums = nums
};
Solution.prototype.reset = function() {
return this.nums
};
Solution.prototype.shuffle = function() {
let res = [...this.nums]
let n = res.length
for(let i = n-1; i >= 0; i--) {
let randIndex = Math.floor(Math.random() * (i + 1))
swap(res, randIndex, i)
}
return res
};
let swap = function(arr, i, j) {
const temp = arr[i]
arr[i] = arr[j]
arr[j] = temp
}
复杂度分析:
时间复杂度:O(n) 空间复杂度:O(n),需要实现 reset功能,原始数组必须得保存一份
更多解答
14.10.3 阿里五面:说下希尔排序的过程?希尔排序的时间复杂度和空间复杂度又是多少?
1959年Shell发明,第一个突破 O(n^2^) 的排序算法,是简单插入排序的改进版。它与插入排序的不同之处在于,它会优先比较距离较远的元素。
插入排序
插入排序的工作原理是通过构建有序序列,对于未排序数据,在已排序序列中从后向前扫描,找到相应位置并插入

代码实现:
function insertionSort(arr) {
let n = arr.length;
let preIndex, current;
for (let i = 1; i < n; i++) {
preIndex = i - 1;
current = arr[i];
while (preIndex >= 0 && arr[preIndex] > current) {
arr[preIndex + 1] = arr[preIndex];
preIndex--;
}
arr[preIndex + 1] = current;
}
return arr;
}
插入算法的核心思想是取未排序区间中的元素,在已排序区间中找到合适的插入位置将其插入,并保证已排序区间数据一直有序。重复这个过程,直到未排序区间中元素为空,算法结束。
复杂度分析:
时间复杂度:O(n^2^) 空间复杂度:O(1)
希尔排序
回顾一下上面的插入排序:
第一趟插入排序后,我们得到的有效序列长度为 2第二趟插入排序后,我们得到的有效序列长度为 3... 直到这个序列有序
所以,如果序列足够乱的话,时间复杂度为 O(n^2^)
希尔排序又是如何优化的喃?
希尔排序又叫缩小增量排序,就是把数列进行分组(组内不停使用插入排序),直至从宏观上看起来有序,最后插入排序起来就容易了(无须多次移位或交换)。
其中组的数量称为 增量 ,显然的是,增量是不断递减的(直到增量为1)
那我们有是如何进行分组喃?
往往的: 如果一个数列有 8 个元素,我们第一趟的增量是 4 ,第二趟的增量是 2 ,第三趟的增量是 1 。如果一个数列有 18 个元素,我们第一趟的增量是 9 ,第二趟的增量是 4 ,第三趟的增量是2 ,第四趟的增量是 1
很明显我们可以用一个序列来表示增量:n/2、(n/2)/2、...、1,每次增量都/2
例如:
let arr = [4, 1, 5, 8, 7, 3]
排序前:
将该数组看成三组( Math.floor(arr.length/2)),分别是:[4, 1],[5, 8],[7, 3]
第一趟排序:
对三组数据分别进行插入排序,因此我们三个数组得到的结果为: [1, 4],[5, 8],[3, 7]
此时数组是这样子的:[1, 4, 5, 8, 3, 7]
第二趟排序:
增量减少了,上面增量是 3,此时增量应该为1了,因此把[1, 4, 5, 8, 3, 7]看成一个数组(从宏观上是有序的了),对其进行插入排序,直至有序
代码实现:
function shellSort(arr) {
let n = arr.length;
for (let gap = Math.floor(n / 2); gap > 0; gap = Math.floor(gap / 2)) {
for (let i = gap; i < n; i++) {
let j = i;
let current = arr[i];
while (j - gap >= 0 && current < arr[j - gap]) {
arr[j] = arr[j - gap];
j = j - gap;
}
arr[j] = current;
}
}
return arr;
}
复杂度分析:
时间复杂度:O(nlogn) 空间复杂度:O(1)
更多解答
14.10.4 排序链表
在 O(n log n) 时间复杂度和常数级空间复杂度下,对链表进行排序。
示例 1:
输入: 4->2->1->3
输出: 1->2->3->4
示例 2:
输入: -1->5->3->4->0
输出: -1->0->3->4->5
解答:采用归并排序
归并排序采用了分治策略,将数组分成2个较小的数组,然后每个数组再分成两个更小的数组,直至每个数组里只包含一个元素,然后将小数组不断的合并成较大的数组,直至只剩下一个数组,就是排序完成后的数组序列。
对应于链表喃?
4->2->1->3
第一步:分割
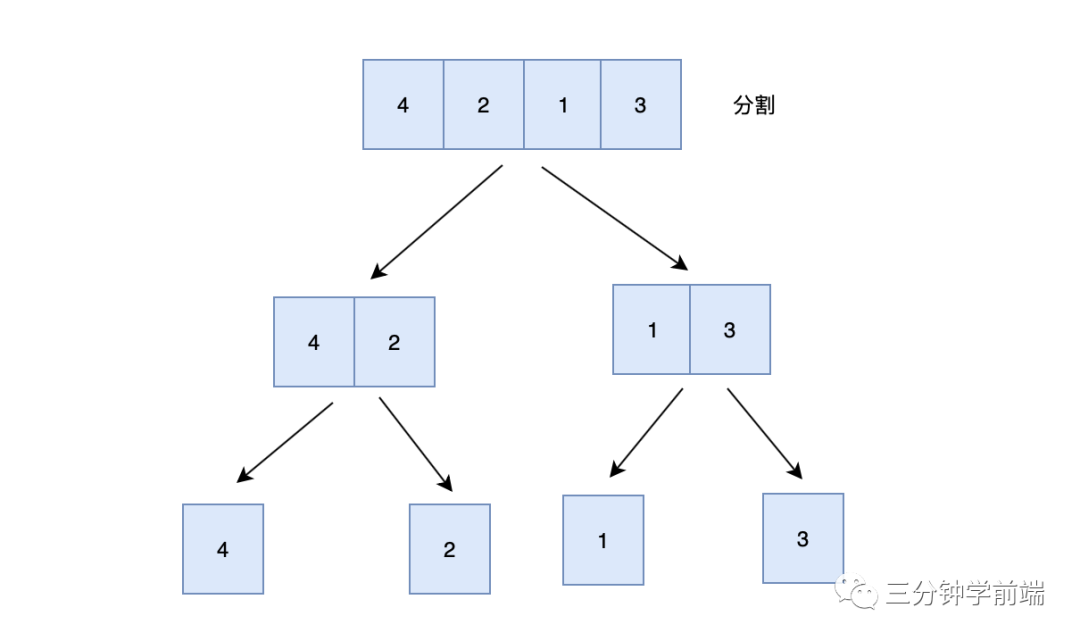
使用快慢指针(双指针法),获取链表的中间节点 根据中间节点,分割成两个小链表 递归执行上一步,直到小链表中只有一个节点
第二步:归并(合并有序链表)
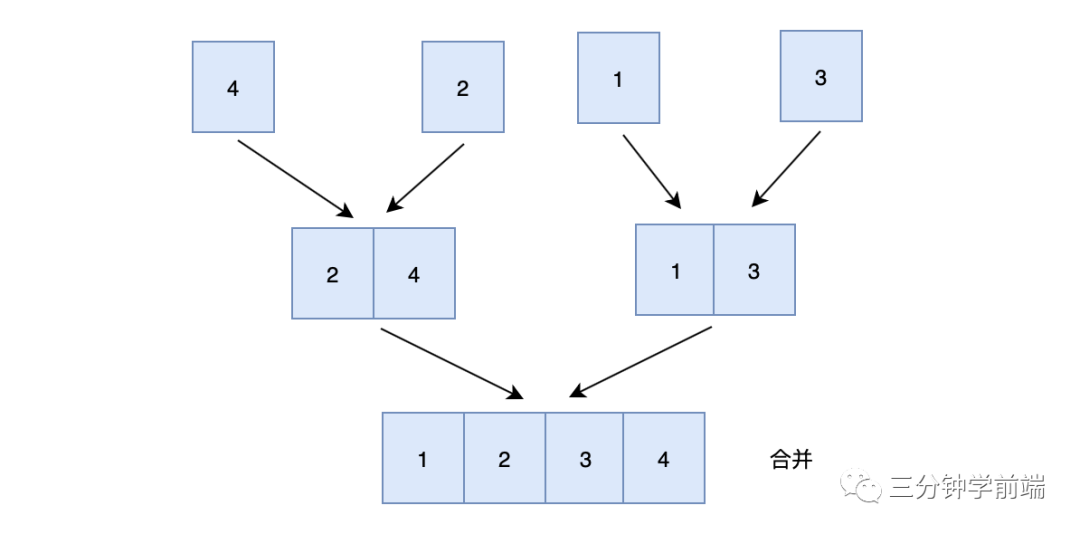
代码实现
let sortList = function(head) {
return mergeSortRec(head)
}
// 归并排序
// 若分裂后的两个链表长度不为 1,则继续分裂
// 直到分裂后的链表长度都为 1,
// 然后合并小链表
let mergeSortRec = function (head) {
if(!head || !head.next) {
return head
}
// 获取中间节点
let middle = middleNode(head)
// 分裂成两个链表
let temp = middle.next
middle.next = null
let left = head, right = temp
// 继续分裂(递归分裂)
left = mergeSortRec(left)
right = mergeSortRec(right)
// 合并两个有序链表
return mergeTwoLists(left, right)
}
// 获取中间节点
// - 如果链表长度为奇数,则返回中间节点
// - 如果链表长度为偶数,则有两个中间节点,这里返回第一个
let middleNode = function(head) {
let fast = head, slow = head
while(fast && fast.next && fast.next.next) {
slow = slow.next
fast = fast.next.next
}
return slow
}
// 合并两个有序链表
let mergeTwoLists = function(l1, l2) {
let preHead = new ListNode(-1);
let cur = preHead;
while(l1 && l2){
if(l1.val < l2.val){
cur.next = l1;
l1 = l1.next;
}else{
cur.next = l2;
l2 = l2.next;
}
cur = cur.next;
}
cur.next = l1 || l2;
return preHead.next;
}
引入递归算法的复杂度分析:
递归算法的时间复杂度:递归的总次数 * 每次递归的数量 递归算法的空间复杂度:递归的深度 * 每次递归创建变量的个数
复杂度分析
时间复杂度:递归的总次数为 T(logn) ,每次递归的数量为 T(n) ,时间复杂度为 O(nlogn) 空间复杂度:递归的深度为 T(logn) ,每次递归创建变量的个数为 T(c) (c为常数),空间复杂度为 O(logn)
关于复杂度分析,请看这篇:前端进阶算法1:如何分析、统计算法的执行效率和资源消耗?
优化递归
使用迭代代替递归,优化时间复杂度:O(logn) —> O(1)
更多解答
14.10.5 扑克牌问题
魔术师手中有一堆扑克牌,观众不知道它的顺序,接下来魔术师:
从牌顶拿出一张牌, 放到桌子上 再从牌顶拿一张牌, 放在手上牌的底部
如此往复(不断重复以上两步),直到魔术师手上的牌全部都放到了桌子上。
此时,桌子上的牌顺序为:(牌顶) 1,2,3,4,5,6,7,8,9,10,11,12,13 (牌底)。
问:原来魔术师手上牌的顺序,用函数实现。
解答:反向推导
假设,原来魔术师手上牌的顺序数组为 origin ,最后放在桌子上的顺序数组为 result
正向的操作为: origin 取出第一个插入 result 前面, origin 再取出第一个换到自己的末尾,如此重复;
反向操作为: origin 最后一个放到自己的第一个前面, result 拿出第一个插入 origin 前面,如此重复;
const calc = (arr) => {
const origin = [];
for (let i = 0; i < arr.length; i++) {
if (origin.length) {
const item = origin.pop();
origin.unshift(item);
}
origin.unshift(result[i])
}
return origin;
}
// 测试
const result = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13]
// 原有顺序
calc(result)
// [13, 2, 12, 6, 11, 3, 10, 5, 9, 1, 8, 4, 7]
更多解答
14.10.6 有效三角形的个数
给定一个包含非负整数的数组,你的任务是统计其中可以组成三角形三条边的三元组个数。
示例 1:
输入: [2,2,3,4]
输出: 3
解释:
有效的组合是:
2,3,4 (使用第一个 2)
2,3,4 (使用第二个 2)
2,2,3
注意:
数组长度不超过1000。 数组里整数的范围为 [0, 1000]。
本题可结合:
字节&leetcode1:两数之和 腾讯&leetcode15:三数之和
一起练习
解法:排序+双指针
我们知道三角形的任意两边之和大于第三边,任意两边之差小于第三边,如果这三条边长从小到大为 a 、 b 、 c ,当且仅当 a + b > c 这三条边能组成三角形
解题思路: 先数组排序,排序完后,固定最长的边,利用双指针法判断其余边
以 nums[nums.length - 1] 作为最长的边 nums[k] ( k = nums.length - 1 )
以 nums[i] 作为最短边,以 nums[nums.length - 2] 作为第二个数 nums[j] ( j = nums.length - 2 ) ,
判断 nums[i] + nums[j] 是否大于 nums[k] ,
nums[i] + nums[j] > nums[k],则:nums[i+1] + nums[j] > nums[k]
nums[i+2] + nums[j] > nums[k]
...
nums[j-1] + nums[j] > nums[k]则可构成三角形的三元组个数加
j-i,并且j往前移动一位(j--), 继续进入下一轮判断nums[i] + nums[j] <= nums[k],则l往后移动一位(nums是增序排列),继续判断
代码实现:
let triangleNumber = function(nums) {
if(!nums || nums.length < 3) return 0
let count = 0
// 排序
nums.sort((a, b) => a - b)
for(let k = nums.length - 1; k > 1; k--){
let i = 0, j = k - 1
while(i < j){
if(nums[i] + nums[j] > nums[k]){
count += j - i
j--
} else {
i++
}
}
}
return count
}
复杂度分析:
时间复杂度:O(n^2^) 空间复杂度:O(n)
注意:
关于 Array.prototype.sort() ,ES 规范并没有指定具体的算法,在 V8 引擎中, 7.0 版本之前,数组长度小于10时, Array.prototype.sort() 使用的是插入排序,否则用快速排序。
在 V8 引擎 7.0 版本之后就舍弃了快速排序,因为它不是稳定的排序算法,在最坏情况下,时间复杂度会降级到 O(n2)。
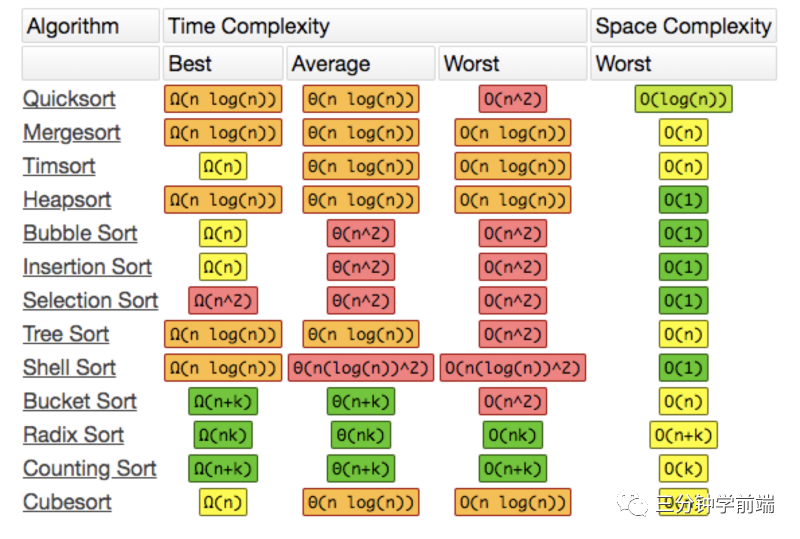
而是采用了一种混合排序的算法:TimSort 。
这种功能算法最初用于Python语言中,严格地说它不属于以上10种排序算法中的任何一种,属于一种混合排序算法:
在数据量小的子数组中使用插入排序,然后再使用归并排序将有序的子数组进行合并排序,时间复杂度为 O(nlogn) 。
 更多解答
更多解答
最后
号内回复:
120 套模版