光学系统的核心--分辨率
点击下方卡片,关注“新机器视觉”公众号
重磅干货,第一时间送达
转载自机器视觉课堂
前言
在机器视觉领域,可以把各个部件划分为光源,镜头,相机,采集卡,算法,运动平台等。各个部件都是系统的有机组合,均有各自的重要性。在实际应用中,成像镜头涉及的光学理论较多,在选型过程比较繁琐。不少拥有多年机器视觉行业经验的工程师依然会对成像镜头在光学系统中的作用感到困惑。
本文尝试从分辨率角度分析镜头在光学系统中的作用解释镜头的重要性。
系统分辨率与像素精度 机器视觉系统最重要的参数是系统分辨率。工程师运用各种理论与技巧,目标就是要提高系统精度。因为一个设备的系统分辨越高,价值越大。一般来说,工程师习惯使用像素精度来表示系统分辨率。
像素精度的概念很简单,即单个像素代表的物理尺寸。
例如相机的像素为10*10,被测物为100mm*100mm,即每个像素代表的物理尺寸为:100mm/10=10mm/像素。
按照这个逻辑,提高系统精度的方法就是提高单位面积的像素比例。
如被测物还是100mm*100mm,相机像素提升为100*100,即每个像素代表的物理尺寸为:100mm/100=1mm/像素。
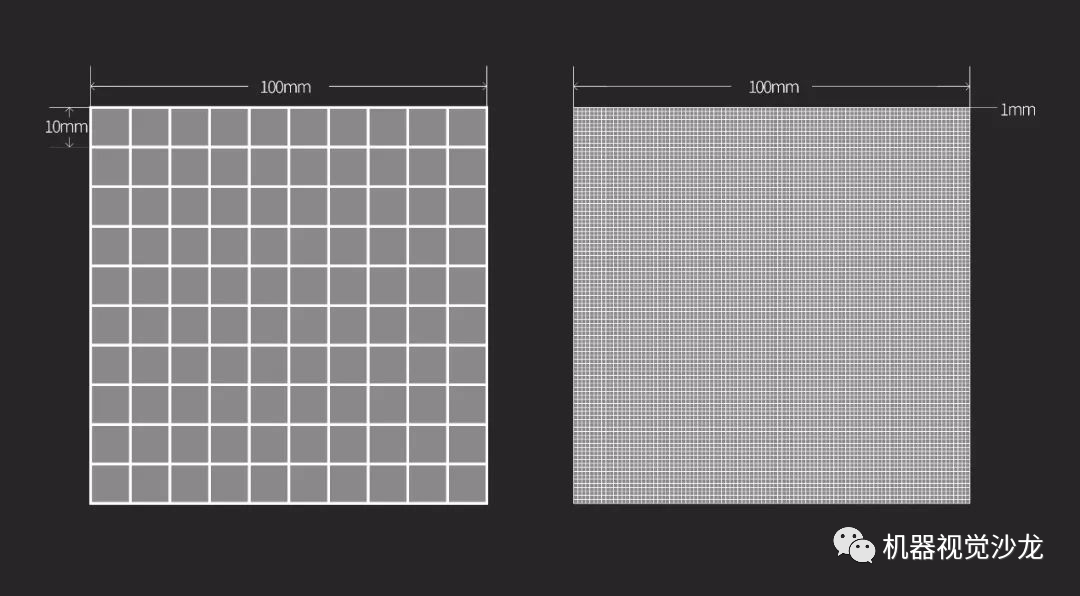
图1:同一个FOV下像素精度的变化
如果按照这个逻辑,单位面积无限增加像素比例,光学系统的精度可以无限提高?
答案显然是不可能的,那这个限制在哪呢?
系统分辨率的“木桶理论” 可以用“木桶理论”来考虑这个问题。光学系统的分辨率(光学分辨率)和相机的图像分辨率是整个成像系统分辨率这个“木桶”上的两块“木板”;成像系统的分辨率等于这两块“木板”中比较短的那块。
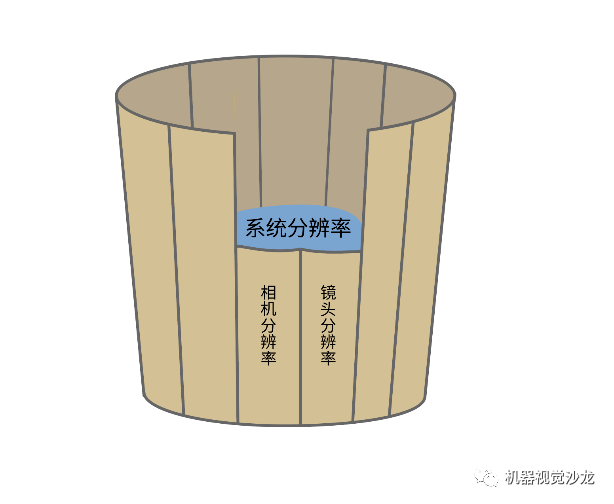
图2:镜头和相机的“木桶理论”
由上述的“木桶理论”可知,存在四种情况:
相机分辨率大于镜头分辨率,提升镜头分辨率,系统分辨率提升;
相机分辨率大于镜头分辨率,提升相机分辨率,系统分辨率不变;
镜头分辨率大于相机分辨率,提升相机分辨率,系统分辨率提升;
镜头分辨率大于相机分辨率,提升镜头分辨率,系统分辨率不变。
平时我们讨论的相机与镜头之间的关系,其实是相机,镜头,系统三者之间的关系。想要理解这三者之间的关系,必须了解分辨率的概念。
相机像元数,相机“像素”与相机分辨率 “像元”“像素”“分辨率”这几个相机相关的术语,业界目前没有十分明确的定义,有些行业还会有显示分辨率,图像分辨率等等不同的概念,比较容易引起混淆。按照笔者理解,相机是没有像素的概念,像素是图像的描述,相机的像元个数等于该相机拍摄的图像像素个数。
像元,图像传感器上能单独感光的物理单元。
像素,数字图像中显示的最小单位。一般相机拍出的图像才会使用像素的概念。相机“像素”的概念并不准确。
分辨率,指分辨率即分辨两个靠近的点的能力,也称为解析力。相机能分辨最小的点就是像元尺寸,可理解为相机的分辨率=像元尺寸。
举个例子:
相机A配备索尼IMX250芯片。其像元个数为2448*2048,其像元尺寸为3.45µm x 3.45 µm。此相机的像元个数为2448*2048,拍摄的图片像素为5013504,相机分辨率为3.45μm。
镜头“像素”与镜头分辨率 为了方便的用户选购镜头,工业镜头厂家往往以“像素”命名镜头。
如相机A能拍摄500万像素的图像,厂家把匹配的镜头命名为500万像素镜头。市面上的标清镜头,高清镜头,1080P镜头,均以相机拍摄的图像像素命名。
但在其他领域,如显微镜,内窥镜,单反镜头,却并没有出现此种现象。显然,以“像素”命名镜头,并不能准确地描述镜头的性能。并且也出现了厂家随意命名的现象,为我们理解镜头分辨率制造了困扰。
真实的镜头分辨率应以MTF曲线体现,图3为MTF曲线的其中一种表达形式。
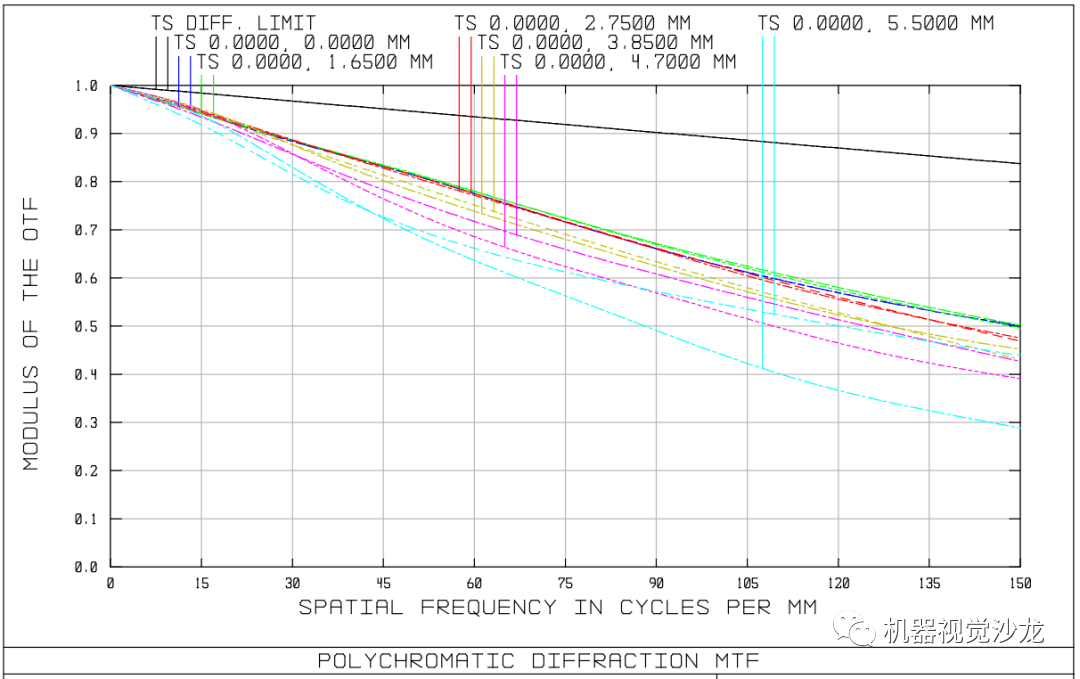
图3:镜头A的MTF曲线图
此MTF曲线的核心内容则是空间频率。即要读懂镜头的分辨率,必须先了解空间频率。
分辨率与空间频率 分辨率可以用空间频率进行量化表达。
空间频率,代表了单位长度内信号的周期数,常用1mm中含有的线对数量表示。一黑一白为1线对。

图4:空间频率
相机分辨率与镜头分辨率可以量化 由上述可知,相机分辨率与镜头分辨率,拥有一个通用的参数——空间频率。换算出相机的空间频率,就可以量化判断系统分辨率到底是由“木桶”的哪块板决定(相机分辨率,镜头分辨率)
相机的空间频率计算公式如下:
相机空间频率(lp/mm)=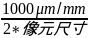
以相机A与镜头A为例。
相机A,可换算其空间频率为:
相机空间频率(lp/mm)=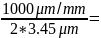 150lp/mm
150lp/mm
镜头A,其空间频率,查看MTF曲线可知为150lp/mm。
镜头A,匹配空间频率大于150lp/mm的相机时,系统分辨率不变;
镜头A,匹配空间频率小于150lp/mm的相机时,系统分辨率下降。
相机A,匹配空间频率大于150lp/mm的镜头时,系统分辨率不变;
相机A,匹配空间频率小于150lp/mm的镜头时,系统分辨率下降;
在相机分辨率越来越高的时代背景下,成像系统分辨率的“压力”也就落在了镜头上,所以更高分辨率(空间频率)的镜头在成像系统中的作用越来越重要。
镜头分辨率与其他参数共同作用影响系统分辨率 镜头分辨率除了跟相机分辨率外,还与其他因素关联,共同影响系统分辨率。
1,镜头分辨率是一个变化的参数
对于一个镜头,其分辨率不是一个恒定不变的值。不同工作距离,不同光圈,不同工作波段,不同像面位置,镜头分辨率会产生变化。
2,镜头分辨率与光源
在设计研发时,一般会对特定波段优化镜头的分辨率。使用特定波长以外的光源,镜头分辨率下降。一般来说,使用特定波段单色光,镜头分辨率会提升。
3,镜头的像方分辨率与物方分辨率
成像镜头的分辨率有多种表达,其中最常用的是像方分辨率与物方分辨率。物方分辨率只是指镜头靠近被测物一方的空间频率,像元分辨率是指靠近相机一方的空间频率。工业定焦镜头一般公开像方分辨率,显微物镜更多公开物方分辨率。
4,镜头分辨率与工作距离
成像镜头的设计主要运用了几何光学原理,一般会对特定的工作距离进行优化。对工业定焦镜头而言,多数产品的最佳工作距离是300mm-600mm,即此工作距离下,镜头分辨率表现最佳,其他工作距离,分辨率表现可能会下降。而安防镜头的最佳工作距离为远距离和无穷远。微距镜头的最佳工作距离为近距离。
5,镜头分辨率与光圈
在一般应用中,镜头分辨率与光圈相关性比较大,减小镜头的光圈,分辨率会提高。但是光圈越小,衍射极限的限制也越明显。
6,镜头分辨率存在物理极限
恩斯特·阿贝博士在19世纪70年代就发现了成像镜头的分辨率极限。可见光镜头的分辨率极限是0.2μm。并且因为材料和工艺问题,一般的成像镜头难以达到这个值。
总结 理解成像镜头的分辨率(空间频率)的计算和评判方法,能更好地理解影响系统精度的核心因素,也为系统升级指明方向。
点击下方卡片,关注“新机器视觉”公众号
重磅干货,第一时间送达
前言
在机器视觉领域,可以把各个部件划分为光源,镜头,相机,采集卡,算法,运动平台等。各个部件都是系统的有机组合,均有各自的重要性。在实际应用中,成像镜头涉及的光学理论较多,在选型过程比较繁琐。不少拥有多年机器视觉行业经验的工程师依然会对成像镜头在光学系统中的作用感到困惑。
本文尝试从分辨率角度分析镜头在光学系统中的作用解释镜头的重要性。
机器视觉系统最重要的参数是系统分辨率。工程师运用各种理论与技巧,目标就是要提高系统精度。因为一个设备的系统分辨越高,价值越大。一般来说,工程师习惯使用像素精度来表示系统分辨率。
像素精度的概念很简单,即单个像素代表的物理尺寸。
例如相机的像素为10*10,被测物为100mm*100mm,即每个像素代表的物理尺寸为:100mm/10=10mm/像素。
按照这个逻辑,提高系统精度的方法就是提高单位面积的像素比例。
如被测物还是100mm*100mm,相机像素提升为100*100,即每个像素代表的物理尺寸为:100mm/100=1mm/像素。

图1:同一个FOV下像素精度的变化
如果按照这个逻辑,单位面积无限增加像素比例,光学系统的精度可以无限提高?
答案显然是不可能的,那这个限制在哪呢?
可以用“木桶理论”来考虑这个问题。光学系统的分辨率(光学分辨率)和相机的图像分辨率是整个成像系统分辨率这个“木桶”上的两块“木板”;成像系统的分辨率等于这两块“木板”中比较短的那块。

图2:镜头和相机的“木桶理论”
由上述的“木桶理论”可知,存在四种情况:
相机分辨率大于镜头分辨率,提升镜头分辨率,系统分辨率提升;
相机分辨率大于镜头分辨率,提升相机分辨率,系统分辨率不变;
镜头分辨率大于相机分辨率,提升相机分辨率,系统分辨率提升;
镜头分辨率大于相机分辨率,提升镜头分辨率,系统分辨率不变。
平时我们讨论的相机与镜头之间的关系,其实是相机,镜头,系统三者之间的关系。想要理解这三者之间的关系,必须了解分辨率的概念。
“像元”“像素”“分辨率”这几个相机相关的术语,业界目前没有十分明确的定义,有些行业还会有显示分辨率,图像分辨率等等不同的概念,比较容易引起混淆。按照笔者理解,相机是没有像素的概念,像素是图像的描述,相机的像元个数等于该相机拍摄的图像像素个数。
像元,图像传感器上能单独感光的物理单元。
像素,数字图像中显示的最小单位。一般相机拍出的图像才会使用像素的概念。相机“像素”的概念并不准确。
分辨率,指分辨率即分辨两个靠近的点的能力,也称为解析力。相机能分辨最小的点就是像元尺寸,可理解为相机的分辨率=像元尺寸。
举个例子:
相机A配备索尼IMX250芯片。其像元个数为2448*2048,其像元尺寸为3.45µm x 3.45 µm。此相机的像元个数为2448*2048,拍摄的图片像素为5013504,相机分辨率为3.45μm。
为了方便的用户选购镜头,工业镜头厂家往往以“像素”命名镜头。
如相机A能拍摄500万像素的图像,厂家把匹配的镜头命名为500万像素镜头。市面上的标清镜头,高清镜头,1080P镜头,均以相机拍摄的图像像素命名。
但在其他领域,如显微镜,内窥镜,单反镜头,却并没有出现此种现象。显然,以“像素”命名镜头,并不能准确地描述镜头的性能。并且也出现了厂家随意命名的现象,为我们理解镜头分辨率制造了困扰。
真实的镜头分辨率应以MTF曲线体现,图3为MTF曲线的其中一种表达形式。

图3:镜头A的MTF曲线图
此MTF曲线的核心内容则是空间频率。即要读懂镜头的分辨率,必须先了解空间频率。
分辨率可以用空间频率进行量化表达。
空间频率,代表了单位长度内信号的周期数,常用1mm中含有的线对数量表示。一黑一白为1线对。

图4:空间频率
由上述可知,相机分辨率与镜头分辨率,拥有一个通用的参数——空间频率。换算出相机的空间频率,就可以量化判断系统分辨率到底是由“木桶”的哪块板决定(相机分辨率,镜头分辨率)
相机的空间频率计算公式如下:
相机空间频率(lp/mm)=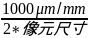
以相机A与镜头A为例。
相机A,可换算其空间频率为:
相机空间频率(lp/mm)=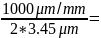 150lp/mm
150lp/mm
镜头A,其空间频率,查看MTF曲线可知为150lp/mm。
镜头A,匹配空间频率大于150lp/mm的相机时,系统分辨率不变;
镜头A,匹配空间频率小于150lp/mm的相机时,系统分辨率下降。
相机A,匹配空间频率大于150lp/mm的镜头时,系统分辨率不变;
相机A,匹配空间频率小于150lp/mm的镜头时,系统分辨率下降;
在相机分辨率越来越高的时代背景下,成像系统分辨率的“压力”也就落在了镜头上,所以更高分辨率(空间频率)的镜头在成像系统中的作用越来越重要。
镜头分辨率除了跟相机分辨率外,还与其他因素关联,共同影响系统分辨率。
1,镜头分辨率是一个变化的参数
对于一个镜头,其分辨率不是一个恒定不变的值。不同工作距离,不同光圈,不同工作波段,不同像面位置,镜头分辨率会产生变化。
2,镜头分辨率与光源
在设计研发时,一般会对特定波段优化镜头的分辨率。使用特定波长以外的光源,镜头分辨率下降。一般来说,使用特定波段单色光,镜头分辨率会提升。
3,镜头的像方分辨率与物方分辨率
成像镜头的分辨率有多种表达,其中最常用的是像方分辨率与物方分辨率。物方分辨率只是指镜头靠近被测物一方的空间频率,像元分辨率是指靠近相机一方的空间频率。工业定焦镜头一般公开像方分辨率,显微物镜更多公开物方分辨率。
4,镜头分辨率与工作距离
成像镜头的设计主要运用了几何光学原理,一般会对特定的工作距离进行优化。对工业定焦镜头而言,多数产品的最佳工作距离是300mm-600mm,即此工作距离下,镜头分辨率表现最佳,其他工作距离,分辨率表现可能会下降。而安防镜头的最佳工作距离为远距离和无穷远。微距镜头的最佳工作距离为近距离。
5,镜头分辨率与光圈
在一般应用中,镜头分辨率与光圈相关性比较大,减小镜头的光圈,分辨率会提高。但是光圈越小,衍射极限的限制也越明显。
6,镜头分辨率存在物理极限
恩斯特·阿贝博士在19世纪70年代就发现了成像镜头的分辨率极限。可见光镜头的分辨率极限是0.2μm。并且因为材料和工艺问题,一般的成像镜头难以达到这个值。
理解成像镜头的分辨率(空间频率)的计算和评判方法,能更好地理解影响系统精度的核心因素,也为系统升级指明方向。
本文仅做学术分享,如有侵权,请联系删文。
