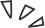计算机科学家证明某些问题确实很难

大数据文摘授权转载自zzllrr小乐
作者:Mordechai Rorvig
译者:zzllrr小乐
去年夏天,三位研究人员朝着回答理论计算机科学中最重要的问题之一迈出了一小步。借用普林斯顿大学高级研究所(IAS)的 Avi Wigderson 的话说,这个问题提出了一个简单而深刻的疑问:我们能解决所有的我们希望解决的问题吗?
更准确地说,计算机科学家想知道我们希望解决的所有问题,是否可以在合理的时间内有效地解决——比如说在宇宙终结之前。如果不可以,它们简直太难了。
许多问题似乎都这么难,但在我们能够用数学证明它们的难度之前,我们无法确信。在去年的一篇论文中,三位计算机科学家表明,一类广泛的问题确实难以有效率地解决,从而提供了该领域一直在寻求的最佳案例之一。
“我们在攀登这座山峰时,正在寻找更稳固的立足点,”华盛顿大学的 Paul Beame 说。“这是这条路线上的另一个立足点。”
研究人员研究的问题只需要加法和乘法。当这些问题仅限于以特定方式求解时(加法和乘法的交替模式),它们变得非常难以解决。
“它极大地改变了我们的知识,”以色列特拉维夫大学的 Amir Shpilka 说。“我们不知道该怎么做。”

计算机科学家 Srikanth Srinivasan(左)、Nutan Limaye(右上)和 Sébastien Tavenas (右下)设计了一种方法来证明某些算术问题确实很难。Srikanth Srinivasan 身着灰色背景的米色衬衫、Nutan Limaye 身着花卉衬衫和 Sébastien Tavenas 身着深色衬衫在户外的照片,身后有金属雕塑。
令人惊讶的是,这些发现不需要新的框架或工具。相反,作者想出了如何绕过由 Wigderson 与耶路撒冷希伯来大学的 Noam Nisan 合作数十年的工作中出现的数学障碍。
丹麦奥胡斯大学的 Srikanth Srinivasan 与哥本哈根 IT 大学的 Nutan Limaye 和法国尚贝里 萨瓦勃朗峰大学的 Sébastien Tavenas 共同撰写了这项新工作,他说:“我们意识到有一种非常笨的方法可以绕过它。”。“而且感觉如果有这么简单的方法可以做我们认为不可能的事情,那么肯定应该有更进一步的方法。”
重要问题
在 1960 年代,在计算机出现了几十年之后,出现了一种令人不安的趋势。科学家们已经成功地创建了算法来让他们的计算机解决各种问题,但有时这些算法花费的时间太长——比实用时间更长。
他们开始怀疑有些问题从根本上很难,无论问题的规模如何。例如,考虑一组由边所连接的点,称为图(graph)。一个重要的问题是确定是否存在一条称为哈密顿路径(Hamiltonian path)的路径,它沿着边行进,每个点只访问一次。按理说,如果增加点(和边)的数量,则需要更长的时间来确定是否存在这样的路径。但是最好的算法随着规模的增加而花费的时间呈指数增长,这使得它们变得不切实际。
许多其他问题似乎也需要指数级的时间。计算机科学家继续证明,任何能够以某种方式有效地解决其中一个难题的算法,都可以转换成解决其他类似困难程度的难题的算法。他们称这类问题为 NP。当 Wigderson 提到“所有我们希望解决的问题”时,他指的是 NP 中的问题,这些问题在许多情况下都会出现。
当然,也有很多看起来不难的问题,没有花指数级时间来解决。计算机科学家表明,这些问题中有许多在某种意义上也是等价的,他们称这一类为 P。他们怀疑 NP 问题确实比 P 问题更难,并且 NP 中的问题永远无法有效地解决。但如果没有证据,总是有可能他们(的想法)是错误的。
计算机科学家开始寻找方法来证明 NP 问题确实更难,研究人员正式将这个问题称为 P 与 NP(P vs NP)。要回答这个问题,只要证明一个难题确实需要指数级的时间就足够了,但他们不知道该怎么做。因此,他们寻找其他可能不那么难以确定难度的途径。
难度有多难?
有一组特定的问题似乎恰到好处,只依赖于加法和乘法。例如,给定一组点,可以仅通过加和乘关于点的数据来计算所有可能的哈密顿路径(如果存在的话)。(如果允许其他操作,例如比较值,也可同样计数,但问题和解会变得更加复杂。)
此外,这组更简单的“算术”问题反映了更大范围的更复杂任务。也就是说,随着问题规模的增加,一些算术问题(如计算哈密顿路径)似乎需要更多的时间。1979 年,哈佛大学的 Leslie Valiant 证明了许多算术问题在难度上是等价的,而其他问题在难易度上(相差一截),也是等价的。后来计算机科学家们以他的名字命名这些类别——分别是 VNP 和 VP。
与 P 与 NP 问题一样,无法证明 VNP 问题的难度。计算机科学家以一种新的形式重新发现了 P 与 NP 问题——VP 与 VNP——只是现在他们有了一个关键优势。VNP 问题比 NP 问题更难,因为它们建立在它们之上:计算路径需要你能够确定路径是否存在。如果想证明某件事是困难的,你就需要尽可能多的困难。
“这比 NP 难,”Shpilka 说。“因此证明这很困难应该更容易。”
在随后的几十年中,计算机科学家在 VP 与 VNP 问题上取得的进展比他们在 P 与 NP 问题上取得的进展要大得多,但其中大部分仅限于 Valiant 创建的称为代数复杂性的子领域。直到 Limaye、Srinivasan 和 Tavenas 最近的工作之前,他们仍然很难判断是否存在任何一般意义上的算术问题。
评估多项式
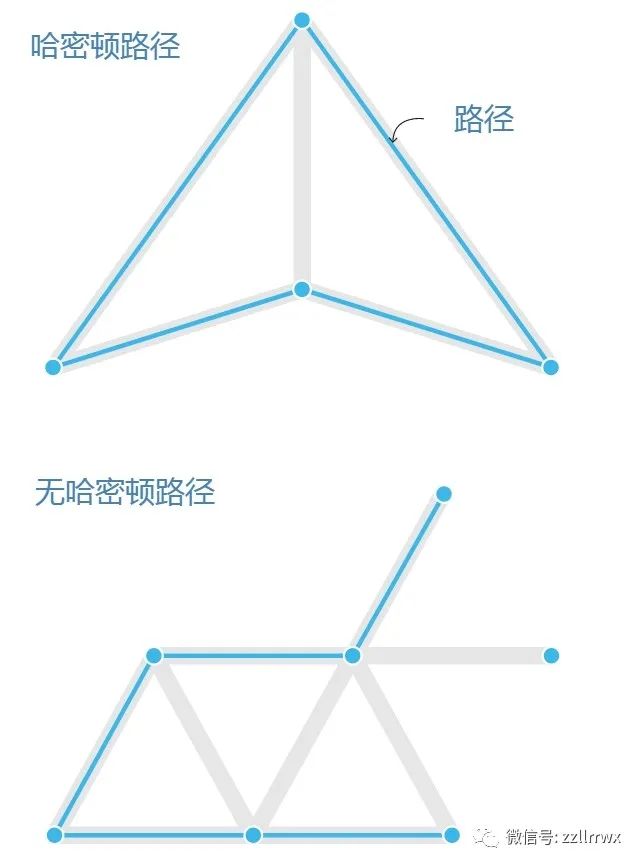
了解计算机科学家如何思考加法和乘法问题,有助于了解这项新工作。从数学上讲,这些问题完全可以被称为多项式的表达式(例如 x² + 5y + 6)捕获,这些表达式由相加和相乘的变量组成。
对于任何特定问题,例如计算哈密顿路径,你可以构建一个表示它的多项式。例如,你可以用一个变量来表示每个点和边,这样当你添加更多点和边时,你也可以向多项式添加更多变量。
为了证明像计算哈密顿路径这样的算术问题很困难,你需要证明当你添加更多点和边时,相应的多项式需要以更多指数级操作来解决。例如,x² 需要一次操作(x 乘以 x),而 x² + y 需要两次操作(x 乘以 x 然后加上 y)。操作的数量称为多项式的大小(size)。
但是多项式的大小很难确定。取多项式 x² + 2x + 1。它的大小似乎为 4(两次乘法和两次加法)。但是多项式可以重写为两个和的乘积,(x + 1)(x + 1),它的操作更少——仍然是两个加法,但现在只有一个乘法。通常,随着问题的规模化和将更多变量添加到多项式中,你可以继续简化和缩小其大小。
在 Valiant 工作几年后,计算机科学家找到了一种方法,可以使问题的大小更易于分析。为此,他们提出了一个称为深度(depth)的属性,它指定多项式在和与乘积之间切换(即交替)的次数。例如,多项式 x² + 2x + 1 的深度为 2,因为它是乘积之和(即 x² 和 2x)。相比之下,表达式 (x + 1)(x + 1) 的深度为 3,因为它在技术上与 0 + (x + 1)(x + 1) 相同,所以它是乘积之和(其中一个乘积由和组成),使整个表达式成为和的乘积的和。
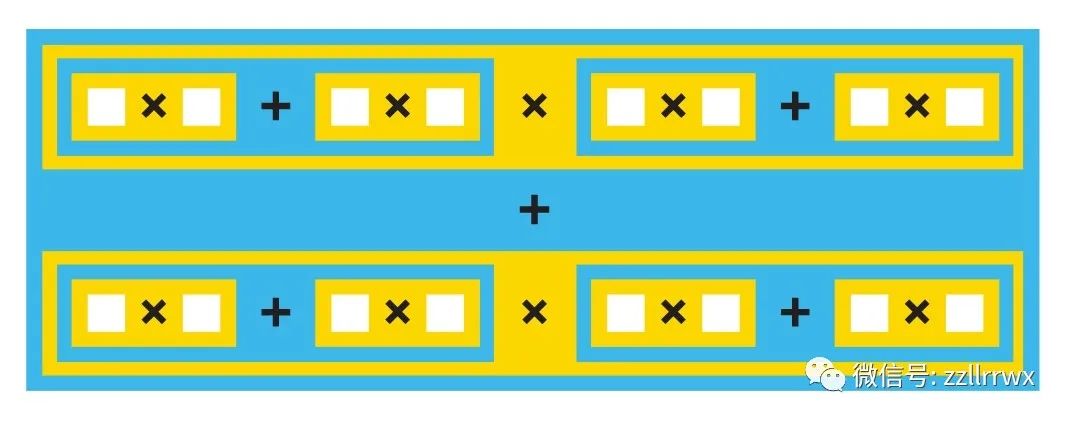
多项式的深度(depth)
许多问题可以表示为多项式,可写成和与乘积交替进行的公式。
什么是深度?
一个多项式中,和与乘积交替的次数。
深度二:乘积的和
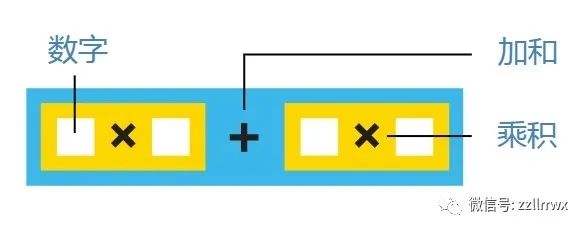
深度三:和的乘积的和
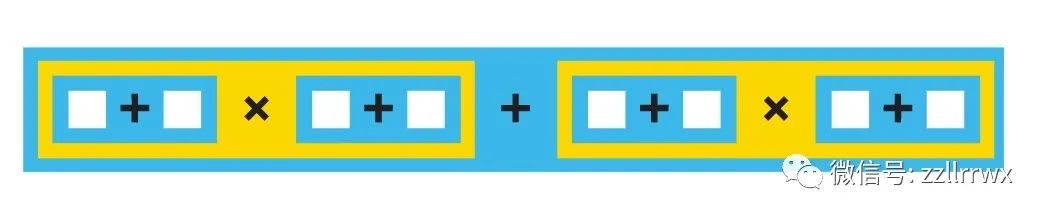
深度四:乘积的和的乘积的和
什么是大小?
多项式中的运算数(做加法、乘法的次数)是它的大小(size)
例如:z⁴+4z³+6z²+4z+1
它的大小是13。

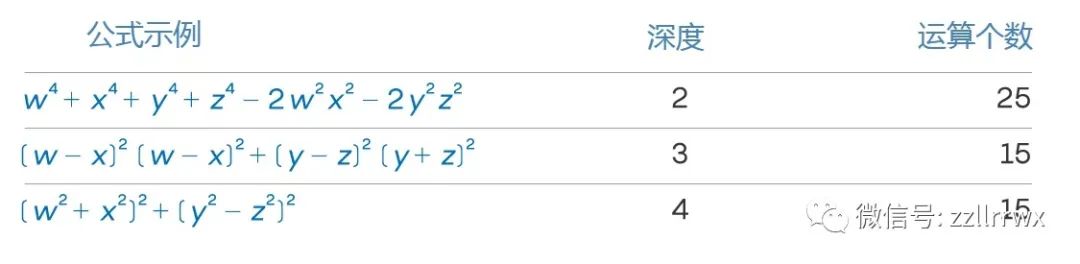
为了简化多项式,计算机科学家将它们限制为一种形式,具有称为恒定深度(constant depth)的属性,其中和与乘积的模式不会随着问题的增长而改变。这使得它们的大小更加静态,因为多项式的大小会随着其深度的增加而减小。某个恒定深度(例如深度三)的表示都称为公式(formulas)。
通过研究恒定深度的多项式以及表示它们的图(称为算术电路arithmetic circuits),计算机科学家能够取得更大的进步。渐渐地,他们有了一系列发现,这些发现最终在新工作中达到顶峰。
令人惊讶的深度
Nisan 和 Wigderson 在 1996 年的一篇论文中迈出了指向新结果的第一步。两人专注于一个经常发生的问题,该问题涉及数字表(称为矩阵matrices)的乘法。他们以两种方式简化了这个问题。首先,他们用恒定深度的公式来表示它——深度三。其次,他们只考虑了具有某种简单结构的公式,其中每个变量的最大指数为 1——这一特性使它们成为“多线性”(multilinear)。(实际上,他们只考虑了这种性质略有变化的公式,称为集合-多线性公式 set-multilinear formulas。)计算机科学家已经知道,某些问题可以转换为这种相对简单的集合-多线性结构,代价是它们的大小呈次指数增加(与指数增长相当的增长率)。
Nisan 和 Wigderson 随后表明,随着矩阵的扩大,矩阵乘法问题需要指数级的时间来解决。换句话说,他们证明了一个重要的问题是困难的,在更广泛的证明困难的事业中取得了显著的胜利。然而,他们的结果是有限的,因为它只适用于具有简单的、集合-多线性结构的公式。
“如果你在代数复杂性之外工作,那可能对你来说意义不大,”Beame说。

Leslie Valiant 在深色背景前身穿方格衬衫的照片
四十多年前,Leslie Valiant 表明,只需要加法和乘法的算术问题可以分为同等难度的类别,现在称为 VNP(用于困难的问题)和 VP(用于更容易的问题)。与 NP 和 P 的更一般的复杂性类别平行。
但在接下来的 20年里,计算机科学家在我们已经看到的基础上,开始更好地理解深度和结构的属性:增加多项式的深度往往会导致其大小减小,并以简单的结构增加它。因此深度和结构与难度进行了一场拔河比赛。
随着时间的推移,计算机科学家使这两个属性之间的平衡行为变得精确。他们表明,将两个深度级别添加到深度三,集合-多线性多项式可以平衡其集合-多线性结构的大小受益。然后,他们可以对此进行推广,以表明如果深度五的结构化公式需要指数时间,那么具有一般非结构化性质的深度三的公式也会如此。
新工作的作者随后表明,矩阵乘法问题的深度五的集合-多线性公式确实以与指数相当的速度增长。通过前面的关系,这意味着一般的深度三公式也需要指数时间。然后他们表明,类似的平衡行为适用于所有深度——不仅仅是三和五。有了这种关系,他们证明了对于同一个问题,任何深度的一般公式的大小都会随着问题的规模增加而以指数速度增长。
在这样做的过程中,他们证明了矩阵乘法只要用一个恒定深度的公式表示,就很难,而无论该深度是多少。虽然之前深入研究过深度三公式,但我们仍然不知道它们是否难——对深度更深的公式的难度(或容易度)我们一无所知。“这是一个巨大的突破,”多伦多大学的 Shubhangi Saraf 说。“这是过去 30 年来许多美好成果的结合。”
这项成果提供了对算术问题何时困难的第一个一般理解 ( 至少,当它被限制为由恒定深度的公式表示时)。研究人员关注的矩阵乘法的具体问题已知是 VP 问题。并且由于已知 VP 问题在不限于恒定深度时相对容易,因此这项成果分离了恒定深度的限制,作为难度的来源。
“该模型受到如此严格的限制,以至于即使在不受限制的世界中应该很容易的事情也会变得困难,”Shpilka 说。
代数复杂性领域的终极问题是,与来自 VP 的问题相比,VNP 问题是否更难。新结果并没有直接说明这一点,因为它只表明恒定深度公式很难。尽管如此,研究人员正在努力在这个结果的基础上再接再厉(以可能让他们得出答案的方式)。
“这可能仍然是一个遥远的目标。很可能是这样,”Saraf说。“但这仍然是 [显示] VP 不等于 VNP 的一个重要里程碑。”
对于更大的 P 与 NP 问题,我们现在可以对终有一天找到答案的前景更加乐观。毕竟,为了解决我们希望解决的问题,我们首先需要知道哪些是无望解决的。
相关报道: