【一天一道Leetcode】矩阵不可变

本篇推文共计2000个字,阅读时间约3分钟。
01
题目描述

题目描述:
给定一个二维矩阵,
计算其子矩形范围内元素的总和,
该子矩阵的
左上角为(row1,col1),右下角为(row2,col2)
如下矩阵所示:
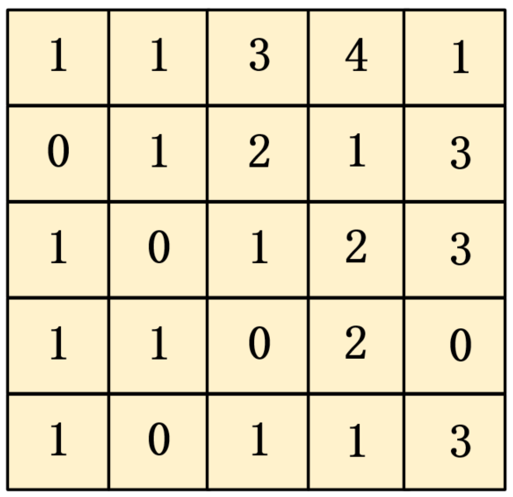
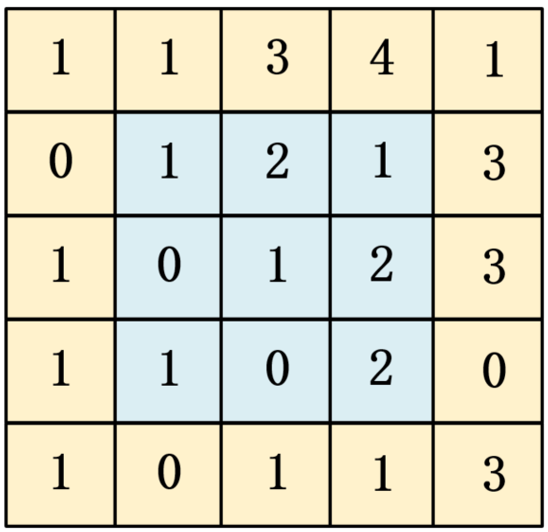
下图中间的子矩阵
左上角(row1,col1)=(1,1),
右下角(row2,col2)=(3,3),
该子矩形区域内元素的总和为10。
这道题是一维前缀和的升级,可以称为二维前缀和。
之前的一维前缀和分析可以查看这篇文章

【一天一道Leetcode】数组不可变
02
代码分析
我们先来分析一下这道题
假设m和n分别是矩阵matrix的行数和列数。
当0≤i<m且0≤j<n时,
f(i,j)为矩阵matrix
以(i,j)为右下角标的子矩阵的元素之和。
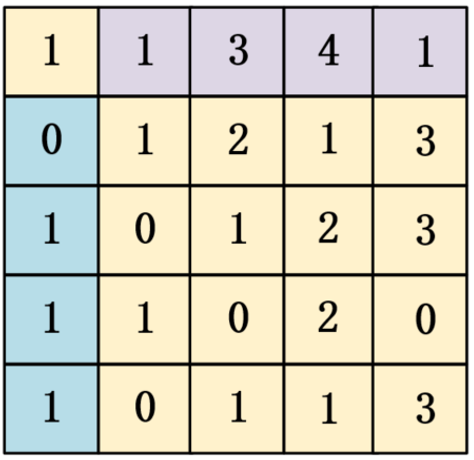
当i=0或j=0时,
计算f(i,j)只需要对矩阵matrix的最上边的行或最左边的列分别计算前缀和即可。
即如下图所示,
f(i,j)为第一行或第一列的元素区域累加数值。
当i和j都大于0时,我们要计算f(i,j)
如下图所示,计算矩阵matrix的前缀和f(2,2)
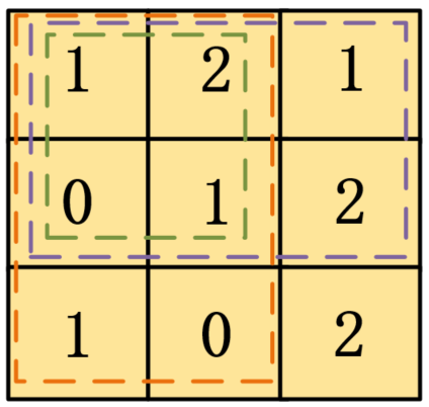
f(2,2)=紫色区域+橙色区域-绿色区域+matrix[2,2]
f(2,2)=f(1,2)+f(2,1)-f(1,1)+matrix[2,2]
即:
f(i,j)=f(i-1,j)+f(i,j-1)-f(i-1,j-1)+matrix[i,j]
根据题意
当row1=0且col1=0时,
sumRange(row1, col1, row2, col2)=f(row2, col2)当row1≠0,col1≠0,row1<=row2,col1<=col2时
由一维前缀和的公式可知
数组(i,j)范围内的元素和为
sumRange(i,j)= presums[j+1]-presums[i]二维矩阵的(row1, col1, row2, col2)区域元素和为
sumRange(row1, col1, row2, col2)=
f(row2, col2)-f(row1-1,col2)-f(row2,col1-1)+f(row1-1,col1-1)用图像来直观说明,如下图矩阵:

我们需要求蓝色方框块的元素和
也即是矩阵中(1,1)到(2,2)区域的元素和
f(1,1,2,2)=f(2,2)-f(0,2)-f(2,0)+f(0,0)
f(2,2)代表绿色方框内的元素和
f(0,2)代表紫色方框内的元素和
f(2,0)代表橙色方框内的元素和
由于f(2,2)-f(0,2)-f(2,0)多减掉了一个f(0,0)
最后需要加上f(0,0)
则最后公式为
f(1,1,2,2)=f(2,2)-f(0,2)-f(2,0)+f(0,0)
我们的代码表示为:
class NumMatrix:
def __init__(self, matrix: List[List[int]]):
if not matrix or not matrix[0]:
pass
else:
m, n = len(matrix), len(matrix[0])
self.sums = [[0] * (n + 1) for i in range(m + 1)]
_sums = self.sums
for i in range(m):
for j in range(n):
_sums[i+1][j+1] = _sums[i][j+1]+_sums[i+1][j]-_sums[i][j]+matrix[i][j]
def sumRegion(self, row1: int, col1: int, row2: int, col2: int) -> int:
_sums = self.sums
return _sums[row2+1][col2+1]-_sums[row1][col2+1]-_sums[row2+1][col1]+_sums[row1][col1]
【年终总结】你好2021,再见2020。

【快速写好毕业论文】你不得不知晓的七个常用文献搜索平台

【秋招纪实录】一篇特别正经的【腾讯】求职经验分享

【一天一道Leetcode】两数之和

【一天一道Leetcode】单调数列

【一天一道Leetcode】数组不可变
你与世界
只差一个
公众号

