一文总结EDA探索性数据分析
Author:张永泰
From:Datawhale
探索性数据分析(Exploratory Data Analysis,EDA)是一种探索数据的结构和规律的一种数据分析方法。其主要的工作包含:对数据进行清洗,对数据进行描述(描述统计量,图表),查看数据的分布,比较数据之间的关系,培养对数据的直觉和对数据进行总结。
EDA可以帮助我们找到适合的数据模型,本文针对文本数据,将进行具体的数据探索性分析讲解。

一、数据及背景
二、实验环境
import numpy as npimport pandas as pdimport matplotlib.pyplot as pltfrom sklearn.model_selection import train_test_splitimport seaborn as snsimport scipyfrom collections import Counter
三、数据探索
首先,利用Pandas对数据进行读取。
df_train = pd.read_csv(train_path, sep='\t')df_test = pd.read_csv(test_path, sep='\t')
3.1 简单查看数据
df_train.head(), len(df_train)
print(len(df_train['text'][0]), type(df_train['text'][0]))df_train.head()
3.2 长度分布
3.2.1 describe
这里与教程中的方法有所不同。vectorize是numpy中很方便的函数,作用和pandas中apply差不多。用法:
np.vectorize(function)(array)输入待处理的array,以及逐元素处理函数function,返回经过处理后的ndarray。原来的array则不受影响。
当前我使用的函数split_df负责将一行数据按空格切分成整数列表,然后计算该列表的长度。
def split_df(df_row):return len(str(df_row).split())len_dist = np.vectorize(split_df)(df_train['text'])len_test_dist = np.vectorize(split_df)(df_test['text'])
使用describe函数查看训练集和测试集中的数据长度分布
print(pd.Series(len_dist).describe())
print(pd.Series(len_test_dist).describe())
训练集共200,000条新闻,每条新闻平均907个字符,最短的句子长度为2,最长的句子长度为57921,其中75%以下的数据长度在1131以下。
测试集共50,000条新闻,每条新闻平均909个字符,最短句子长度为14,最长句子41861,75%以下的数据长度在1133以下。
训练集和测试集就长度来说似乎是同一分布。
3.2.2 直方图
绘制直方图查看训练集和测试集中的数据长度分布
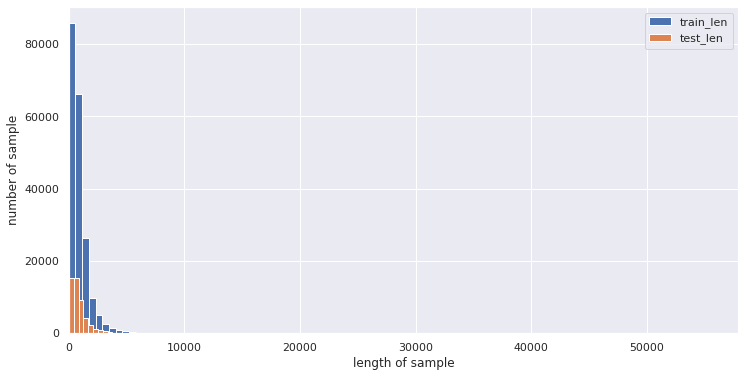
fig, ax = plt.subplots(1,1,figsize=(12,6))ax = plt.hist(x=len_dist, bins=100)ax = plt.hist(x=len_test_dist, bins=100)plt.xlim([0, max(max(len_dist), max(len_test_dist))])plt.xlabel("length of sample")plt.ylabel("number of sample")plt.legend(['train_len','test_len'])plt.show()
使用seaborn绘制更好的图。seaborn计算的纵坐标是频率,而不是出现次数。由于训练集和测试集的数据量不一样,因此用频率更加科学、更能看出是否符合同一分布。
plt.figure(figsize=(15,5))ax = sns.distplot(len_dist, bins=100)ax = sns.distplot(len_test_dist, bins=100)plt.xlim([0, max(max(len_dist), max(len_test_dist))])plt.xlabel("length of sample")plt.ylabel("prob of sample")plt.legend(['train_len','test_len'])
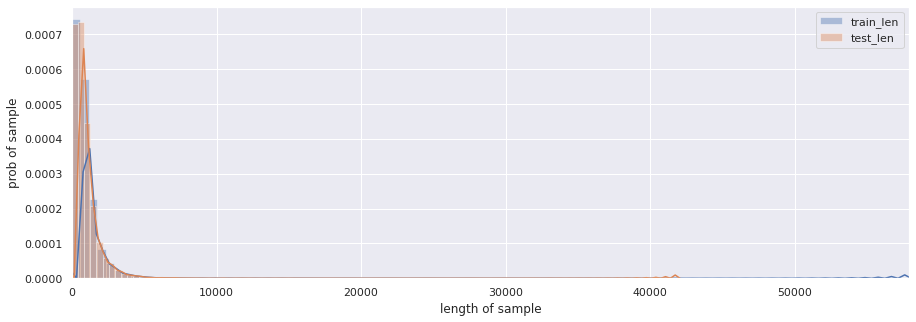
通过直方图,我们能直观感受到训练集和测试集的长度分布都属于右偏分布。按理说分析到这份儿上就该停了。
3.2.3 同分布验证
import scipyscipy.stats.ks_2samp(len_dist, len_test_dist)Ks_2sampResult(statistic=0.004049999999999998, pvalue=0.5279614323123156)
P值为0.52,比指定的显著水平(假设为5%)大,我们认为二者同分布。
3.2.4 截断位置
测量拟合分布的均值和方差sigma原则:
原则:数值分布在中的概率为0.6526;
原则:数值分布在中的概率为0.9544;
原则:数值分布在中的概率为0.9974;
由于“小概率事件”和假设检验的基本思想 “小概率事件”通常指发生的概率小于5%的事件,认为在一次试验中该事件是几乎不可能发生的。由此可见X落在以外的概率小于千分之三,在实际问题中常认为相应的事件是不会发生的,基本上可以把区间看作是随机变量X实际可能的取值区间,这称之为正态分布的“”原则。
log_len_dist = np.log(1+len_dist)log_len_test_dist = np.log(1+len_test_dist)plt.figure(figsize=(15,5))ax = sns.distplot(log_len_dist)ax = sns.distplot(log_len_test_dist)plt.xlabel("log length of sample")plt.ylabel("prob of log")plt.legend(['train_len','test_len'])
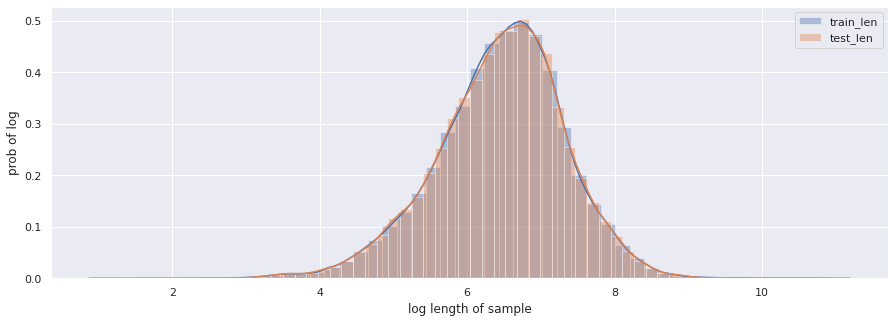
先验证训练集分布为正态分布:
_, lognormal_ks_pvalue = scipy.stats.kstest(rvs=log_len_dist, cdf='norm')print('P value is ', lognormal_ks_pvalue)P value is 0.0
之前我们把数据log了一下,但是这里有更科学的变换方式。log只是box-cox变换的特殊形式。我们使用box-cox变换再次做一下验证,是否为正态分布:
trans_data, lam = scipy.stats.boxcox(len_dist+1)scipy.stats.normaltest(trans_data)NormaltestResult(statistic=1347.793358118494, pvalue=2.1398873511704724e-293)
但总归是要猜一个截断值的。看log图上8.5的位置比较靠谱。np.exp(8.5)=4914约等于5000,因此我初步决定把截断长度定为5000。
3.3 类别信息
3.3.1 简单查看类别信息表
text-split,将text字段分词
len,每条新闻长度
first_char,新闻第一个字符
last_char,新闻最后一个字符
most_freq,新闻最常出现的字符
df_train['text_split'] = df_train['text'].apply(lambda x:x.split())df_train['len'] = df_train['text'].apply(lambda x:len(x.split()))df_train['first_char'] = df_train['text_split'].apply(lambda x:x[0])df_train['last_char'] = df_train['text_split'].apply(lambda x:x[-1])df_train['most_freq'] = df_train['text_split'].apply(lambda x:np.argmax(np.bincount(x)))df_train.head()

count,该类别新闻个数
len_mean,该类别新闻平均长度
len_std,该类别新闻长度标准差
len_min,该类别新闻长度最小值
len_max,该类别新闻长度最大值
freq_fc,该类别新闻最常出现的第一个字符
freq_lc,该类别新闻最常出现的最后一个字符
freq_freq,该类别新闻最常出现的字符
df_train_info = pd.DataFrame(columns=['count','len_mean','len_std','len_min','len_max','freq_fc','freq_lc','freq_freq'])for name, group in df_train.groupby('label'):count = len(group) # 该类别新闻数len_mean = np.mean(group['len']) # 该类别长度平均值len_std = np.std(group['len']) # 长度标准差len_min = np.min(group['len']) # 最短的新闻长度len_max = np.max(group['len']) # 最长的新闻长度freq_fc = np.argmax(np.bincount(group['first_char'])) # 最频繁出现的首词freq_lc = np.argmax(np.bincount(group['last_char'])) # 最频繁出现的末词freq_freq = np.argmax(np.bincount(group['most_freq'])) # 该类别最频繁出现的词df_train_info.loc[name] = [count,len_mean,len_std,len_min,len_max,freq_fc,freq_lc,freq_freq]df_train_info
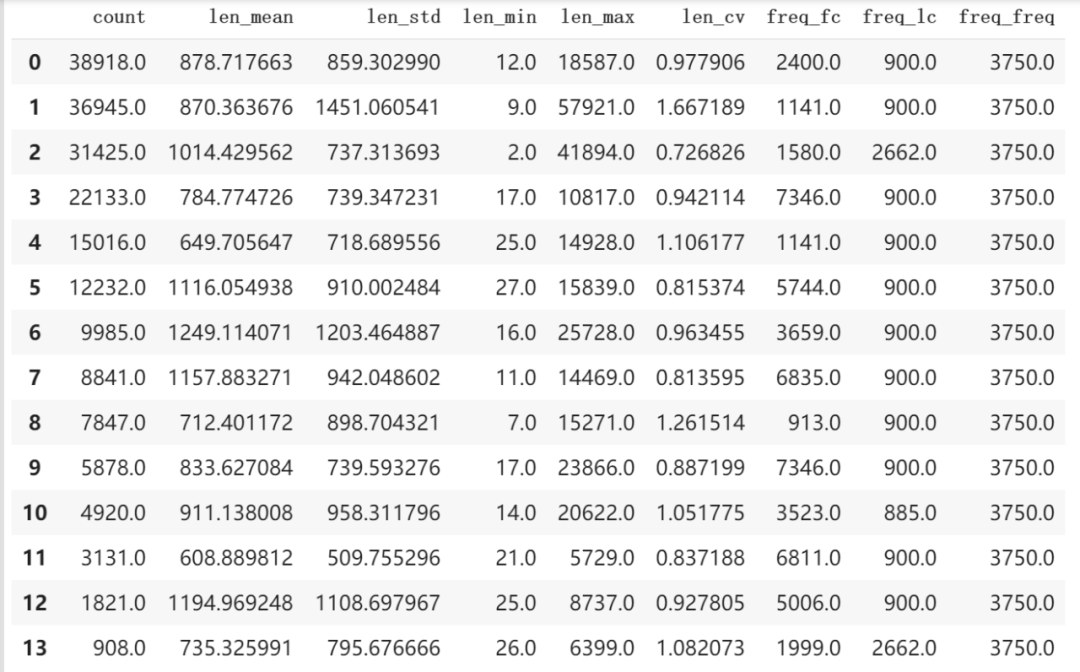
3.3.2 类别分布
在数据集中标签的对应的关系如下
label_2_index_dict = {'科技': 0, '股票': 1, '体育': 2, '娱乐': 3, '时政': 4, '社会': 5, '教育': 6, '财经': 7, '家居': 8, '游戏': 9, '房产': 10, '时尚': 11, '彩票': 12, '星座': 13}index_2_label_dict = {v:k for k,v in label_2_index_dict.items()}plt.figure()plt.bar(x=range(14), height=np.bincount(df_train['label']))plt.xlabel("label")plt.ylabel("number of sample")plt.xticks(range(14), list(index_2_label_dict.values()), fontproperties=zhfont, rotation=60)plt.show()
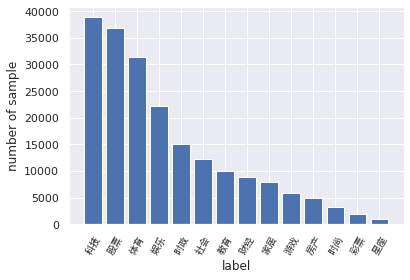
赛题的数据集类别分布存在较为不均匀的情况。在训练集中科技类新闻最多,其次是股票类新闻,最少的新闻是星座新闻。
科技类新闻最多,星座类新闻最少。这个国家的人大部分是唯物主义者哈,神秘学受众比较少(啊这,我在分析什么?)。
由于类别不均衡,会严重影响模型的精度。但是我们也是有办法应对的。
3.3.3 类别长度
df_train['len'] = df_train['text'].apply(lambda x: len(x.split()))plt.figure()ax = sns.catplot(x='label', y='len', data=df_train, kind='strip')plt.xticks(range(14), list(index_2_label_dict.values()), fontproperties=zhfont, rotation=60)
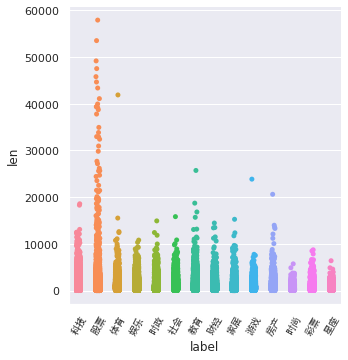
在散点图中,股票类新闻的长度都飘到天上去了,可以看出股票分析类文章真的很容易写得又臭又长啊(发现:不同类别的文章长度不同,可以把长度作为一个Feature,以供机器学习模型训练)!
3.4 字符分布
训练集中总共包括6869个字,最大数字为7549,最小数字为0,其中编号3750的字出现的次数最多,编号3133的字出现的次数最少,仅出现一次。
# 内存警告!!!没有8G内存不要运行该代码all_lines = ' '.join(list(df_train['text']))word_count = Counter(all_lines.split(" "))word_count = sorted(word_count.items(), key=lambda d:d[1], reverse=True)print(len(word_count))# 6869print(word_count[0])# ('3750', 7482224)print(word_count[-1])# ('3133', 1)
下面代码统计了不同字符在多少个句子中出现过,其中字符3750、字符900和字符648在20w新闻的覆盖率接近99%,很有可能是标点符号。
%%timedf_train['text_unique'] = df_train['text'].apply(lambda x: ' '.join(list(set(x.split(' ')))))all_lines = ' '.join(list(df_train['text_unique']))word_count = Counter(all_lines.split(" "))word_count = sorted(word_count.items(), key=lambda d:int(d[1]), reverse=True)# 打印整个训练集中覆盖率前5的词for i in range(5):print("{} occurs {} times, {}%".format(word_count[i][0], word_count[i][1], (word_count[i][1]/200000)*100))

四、分析总结
训练集共200,000条新闻,每条新闻平均907个字符,最短的句子长度为2,最长的句子长度为57921,其中75%以下的数据长度在1131以下。测试集共50,000条新闻,每条新闻平均909个字符,最短句子长度为14,最长句子41861,75%以下的数据长度在1133以下。 训练集和测试集就长度来说似乎是同一分布,但是不属于正态分布。 赛题的数据集类别分布存在较为不均匀的情况。在训练集中科技类新闻最多,其次是股票类新闻,最少的新闻是星座新闻。需要用采样方法解决。文章最长的是股票类新闻。不同类别的文章长度不同,可以把长度和句子个数作为一个Feature,以供机器学习模型训练。 训练集中总共包括6869个字,最大数字为7549,最小数字为0,其中编号3750的字出现的次数最多,编号3133的字出现的次数最少,仅出现一次,其中字符3750、字符900和字符648在20w新闻的覆盖率接近99%,很有可能是标点符号。 900很有可能是句号,2662和885则很有可能为感叹号和问号,3750出现频率很高但是基本不在新闻最后出现,因此初步判断为逗号。按照这种划分,训练集中每条新闻平均句子个数约为19。 在训练集中,不同类别新闻出现词汇有特色。但是需要把共有的常用词停用。自然想到利用TF-IDF编码方式。
往期精彩:
