数学为什么需要证明?
日期 : 2021年04月11日
正文共 :7351字

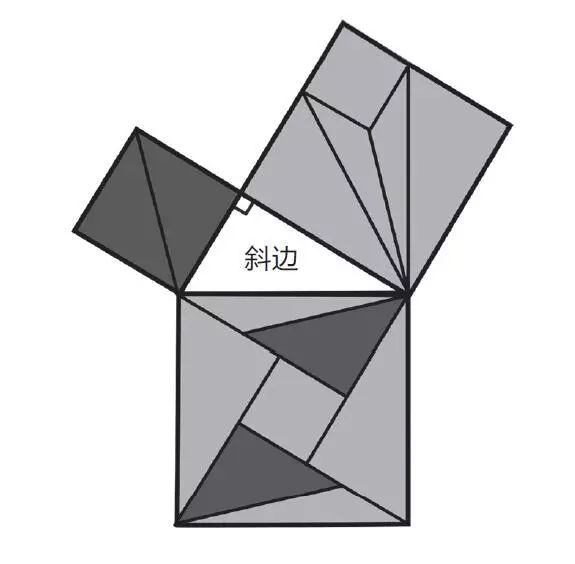
1. 任意两点能够定义一条线段。
2. 一条线段能够向两端无限延伸。
3. 给定一条线段,能够画出一个以该线段的一个端点为圆心,线段长度为半径的圆。
4. 所有的角度都可叠加。
5. 若一条直线与两条直线相交,在某一侧的内角和小于两个直角和,那么这两条直线在各自不断地延伸后,会在内角和小于两直角的一侧相交。
— THE END —

评论
 下载APP
下载APP日期 : 2021年04月11日
正文共 :7351字


1. 任意两点能够定义一条线段。
2. 一条线段能够向两端无限延伸。
3. 给定一条线段,能够画出一个以该线段的一个端点为圆心,线段长度为半径的圆。
4. 所有的角度都可叠加。
5. 若一条直线与两条直线相交,在某一侧的内角和小于两个直角和,那么这两条直线在各自不断地延伸后,会在内角和小于两直角的一侧相交。
— THE END —
