引言

本着“凡我不能创造的，我就不能理解”的思想，本系列文章会基于纯Python以及NumPy从零创建自己的深度学习框架，该框架类似PyTorch能实现自动求导。

要深入理解深度学习，从零开始创建的经验非常重要，从自己可以理解的角度出发，尽量不适用外部完备的框架前提下，实现我们想要的模型。本系列文章的宗旨就是通过这样的过程，让大家切实掌握深度学习底层实现，而不是仅做一个调包侠。

本文对逻辑回归的原理进行简单的介绍，包含公式推导。逻辑回归是可以作为分类任务的基准，也是神经网络的基石。一个神经网络可以看成是一系列的逻辑回归组成。所以掌握逻辑回归就相当重要。

回归与分类

我们前面学习的线性回归属于回归问题，今天介绍的逻辑回归属于分类问题。

回归：预测一个连续值；

分类：预测一个离散值；

逻辑回归虽然名字中包含回归，实际上处理的是分类问题，为啥名字这么奇怪呢，有历史原因，这里就不深究了。

逻辑回归用于处理二分类问题，所谓二分类问题，就是分类的类别只有两个的问题。比如判断邮件是否为垃圾、情绪分析中的情绪是正向的还是负向的等。

那么逻辑回归是如何处理二分类问题的呢？答案就是通过Sigmoid函数。

机器学习分类器的核心组件

逻辑回归是一种基于监督学习的分类器。机器学习分类器需要一个训练集，包含个输入/输出对。一个分类机器学习系统有四个组件：

1. 输入的特征表示 对于每个输入样本，可以表示为特征向量，表示输入的第个特征，有时简记为
2. 计算估计类别的分类函数，通过
3. 一个学习的目标函数，通过计算训练样本上的最小化误差
4. 一个优化目标函数的算法，常用的是随机梯度下降法

Sigmoid函数

我们先来看下输入的表示，通常我们有很多个输入样本。对于第个样本，可以表示为特征向量，这里假设有个特征。

考虑一个输入样本，表示为特征向量，输出可能是或，其中表示属于某个类别的话，那么就表示不属于那个类别。

逻辑回归从一个训练集中学习权重向量和一个偏置。每个权重与输入样本中的一个特征绑定，最后加上偏置项。权重和偏置项都是实数。

为了判断类别，首先让每个特征乘上对应的权重，然后加上，得到一个实数，表示属于该类别的依据。

实数越大，表示该特征对属于该类别的贡献度越大。我们也可以通过线性代数中的点乘的方式来简化这个公式：

但是，这样得到的显然不是一个概率值，如果细心的童鞋可能回发现，这不就是线性回归的公式吗。没错，但是逻辑回归需要利用一个函数来把一个属于到的实数值转换为之间的概率值。

这个函数就是Sigmoid函数，记为，也称为逻辑函数。

它的公式如下：

它的函数图像如下：

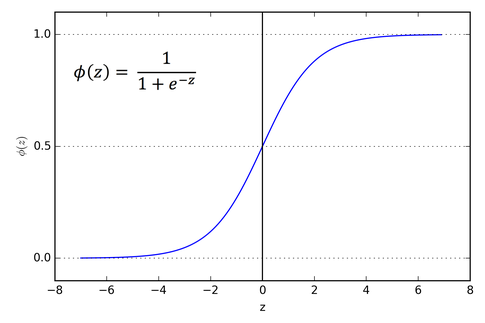
Sigmoid函数的优点是：它可以将任意实数压缩到之间，这刚好符合概率的定义。同时它是可导的。

为了让Sigmoid函数的输出刚好是一个概率，我们要确保。我们来看是否具有这种性质：

也就是说，Sigmoid函数还有以下性质：

所以有。

决策边界

给定输入，我们已经知道了如何取计算属于类别的概率。

但我们如何判断是否属于类别呢？直观地，如果概率，我们就说它属于该类别，否则不属于该类别。那么就是决策边界。

逻辑回归中的损失函数

我们知道每个样本对应的正确标签。根据公式(4)算的是对真实的估计，我们想让估计和真实越接近越好。这里的“接近”衡量的是距离，我们称这种距离为损失(loss)或者代价(cost)。计算损失或代价的函数为损失函数或代价函数。

给定样本，我们需要一个损失函数来衡量类器的输出()与真实输出有多近。可以记为：

该函数倾向于模型更可能将训练样本分类成正确的类别。这称为条件最大似然估计：我们选择参数来最大化训练数据中给定样本属于真实标签的对数概率。此时对应的损失函数为负对数似然损失，通常称为交叉熵损失。

对于单个样本，我们希望学到权重能最大化正确类别概率。由于只有两个离散的输出(0或1)，这是一个伯努利分布，我们可以将分类器为一个样本产生的概率表示为如下：

如果正确类别，那么上式右边简化为；如果，那么简化为。

我们把等式两端取对数，取对数并不会改变单调性：

上式描述了一个应该最大化的对数似然。为了让它变成损失函数，我们增加一个负号，变成了交叉熵损失(loss of cross entropy):

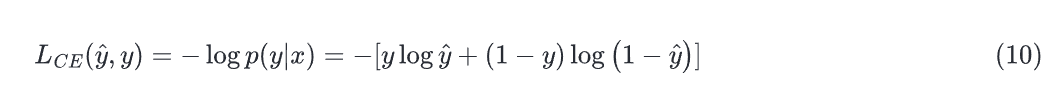
最终，我们代入:

为什么最小化这个负对数似然就能实现我们想要的结果？一个完美的分类器会将正确的输出标记为1，错误的输出标记为0。意味着，如果，输出越高，分类器越好，输出的越低，分类器越差；如果，越大，分类器越好。

的负对数(真实)或的负对数(真实)是一个方便的损失指标，因为它可以是从0(，代表没有损失)到无穷大()。该损失函数也确保正确答案的概率最大化，错误答案的概率最小化；由于它们之和等于1，正确答案概率的任何增加都是以减少错误答案为代价的。

梯度下降

使用梯度下降的目的是找到最优的权重：最小化损失函数。在下面的公式中，我们看到损失函数由权重参数化的，我们将在机器学习中将其称为（在逻辑回归中）。所以目标是找到权重集能最小化损失函数，平均所有的样本就是：

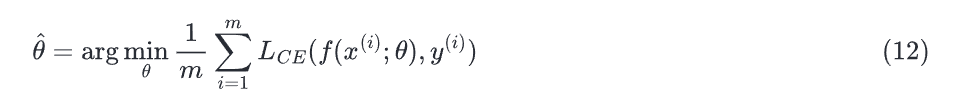
我们如何找到这个损失函数的最小值呢？梯度下降是一种方法，通过计算函数的斜率向哪个方向（在参数θ的空间）上升得最陡峭，并朝着相反的方向移动来找到函数的最小值。

对于逻辑回归，损失函数是一个凸函数，即只有一个最小值，所以梯度下降能保证从任意点都能达到最小值。而多层神经网络的损失函数时非凸的，可能受困于局部极小值。

在一个真实的逻辑回归中，参数向量的元素个数可能很多，即每个特征都有对应的权重。对于中的每个维度/变量(加上偏置)，梯度将告诉我们该变量的斜率的部分。在每个维度，我们描述斜率为损失函数的偏导。本质上我们想知道：在变量上的一个小改变会影响总损失函数多少？

因此，在形式上，多变量函数的梯度是一个向量，其中每个元素都表示相对于对应变量的偏导。我们将使用来指梯度，并将表示为:

基于梯度更新参数 的式子为：

逻辑回归的梯度

为了更新参数，我们需要梯度的定义，我们知道逻辑回归的交叉熵损失函数为：

要求上式对某个参数的导数，我们回顾一下：

我们知道，。我们先计算，令:

我们计算损失函数对某个权重的梯度：

最后得到的结果很简单，描述的就是预测值减去真实值乘上对应的输出。

总结

本文我们了解了逻辑回归的原理，下篇文章就来实现它。