算法的重要性,我就不多说了吧,想去大厂,就必须要经过基础知识和业务逻辑面试+算法面试。所以,为了提高大家的算法能力,这个公众号后续每天带大家做一道算法题,题目就从LeetCode上面选 !
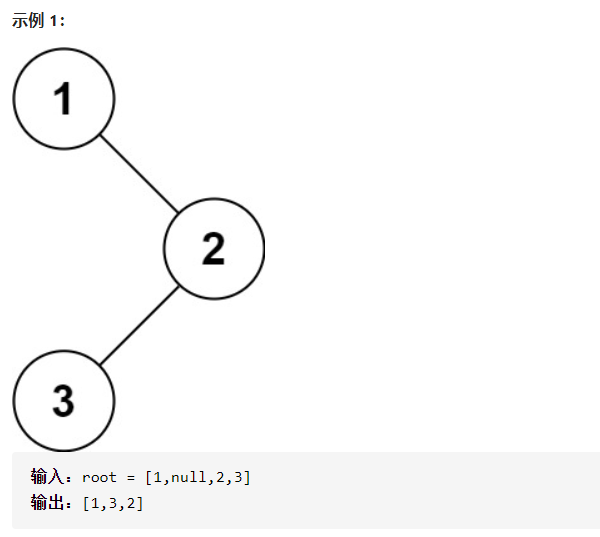
今天和大家聊的问题叫做 二叉树的中序遍历,我们先来看题面:
https://leetcode-cn.com/problems/binary-tree-inorder-traversal/
Given the root of a binary tree, return the inorder traversal of its nodes' values.
题意
给定一个二叉树的根节点 root ,返回它的 中序 遍历。用递归做这道题非常简单,你能不用递归实现吗?解题
https://www.cnblogs.com/techflow/p/13587858.html我们先来介绍一下二叉树的中序遍历,二叉树有三种遍历方式,分别是先序、中序和后序。对于初学者而言,可能会觉得这三种顺序傻傻分不清楚,不知道它们之间有什么分别。其实说白了非常简单,遍历方式其实指的是我们在递归遍历的时候的选择顺序。假设我们目前递归到的节点是u,它有左右两个孩子。在保证左孩子一定先于右孩子访问的前提下,我们有三种策略。第一种是先把u加入访问序列,之后再分别遍历左右子树,第二种是先递归遍历左子树,然后把u加入访问序列,最后再遍历右子树。第三种策略是先递归遍历左右子树,最后再把u加入访问序列。这三种策略之间有什么不同呢?其实最大的不同就在于u加入访问序列的顺序不同,如果是先加入u再访问,那么就是先序。如果是先访问了左子树再来加入u,则是中序,最后如果是先递归了左右子树,最后再加入u,则是后序。说白了也就是u先加入就是先序,中间加入就是中序,最后加入就是后序。如果你还觉得有点蒙的话,我们来看下代码就非常清晰了。# 先序
def dfs(u):
visited.append(u)
dfs(u.left)
dfs(u.right)
# 中序
def dfs(u):
dfs(u.left)
visited.append(u)
dfs(u.right)
# 后序
def dfs(u):
dfs(u.left)
dfs(u.right)
visited.append(u)
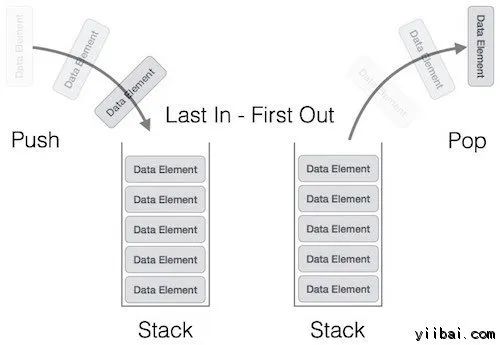
但是题目当中要求我们不通过递归来实现,这该怎么办呢?其实也有办法,我们需要从递归的实现原理入手。我们知道在编译器内部,当我们从一个函数调用另外一个函数的时候,这些函数的信息会被存储在一个栈结构内。栈中间的每一个节点会记录函数的名称以及它目前运行的位置,以及一些中间变量等等。所以当我们递归的时候,其实就是当前的函数不停的入栈的过程。比如我们dfs函数在第5行代码处递归调用了dfs函数,那么编译器内部的堆栈会记录[(dfs, 5), (dfs, 1)]。如果我们在dfs的第一行又调用了sum函数,那么编译器又会把sum这个函数加入堆栈,变成:[(dfs, 5), (dfs, 1), (sum, 1)]。当函数执行完成之后,会从栈中弹出。简而言之,递归其实就是利用编译器自行维护的栈结构来简化我们代码和功能的编写。既然这道题当中要求我们不能使用递归,那么我们就只能自己来使用栈来模拟这个过程了。由于我们自己需要维护栈当中的元素,使得整个过程会稍微复杂一些。在这道题目当中,我们使用栈来记录树上的节点。栈顶的节点即是当前访问的节点。class Solution:
def inorderTraversal(self, root: TreeNode) -> List[int]:
ret = []
stack = []
stack.append(root)
while len(stack) > 0:
# 获取栈顶顶点
cur = stack[-1]
if cur is None:
stack.pop()
continue
# 如果左孩子存在,那么优先遍历左孩子
if cur.left is not None:
stack.append(cur.left)
# 把左指针置为空,防止死循环
# 这里也可以用set来维护
cur.left = None
continue
# 左边遍历结束之后加入序列
ret.append(cur.val)
stack.pop()
if cur.right is not None:
stack.append(cur.right)
return ret
如果只是二叉树的遍历,那这个谁都会,但如果不能使用递归,那么就很考验硬实力了。需要我们对递归的底层原理有深入的理解,并且熟悉栈这个数据结构的使用。这段代码的逻辑不难理解,但实现还是挺锻炼人的,推荐大家试试。好了,今天的文章就到这里,如果觉得有所收获,请顺手点个在看或者转发吧,你们的支持是我最大的动力。