吃透空洞卷积(Dilated Convolutions)
重磅干货,第一时间送达
导读
空洞卷积在图像分割需要增加感受野同时保持特征图的尺寸的需求中诞生,本文详细介绍了空洞卷积的诞生、原理、计算过程以及存在的两个潜在的问题,帮助大家将空洞卷积这一算法“消化吸收”。
一、空洞卷积的提出

二、空洞卷积的原理
 卷积为例,展示普通卷积和空洞卷积之间的区别,如图2所示
卷积为例,展示普通卷积和空洞卷积之间的区别,如图2所示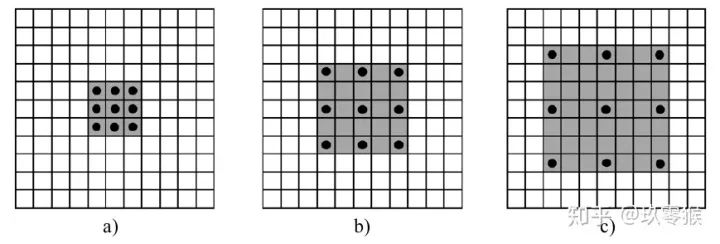
 的卷积核,灰色地带表示卷积后的感受野(后面有相关计算公式,这里都是一层卷积的,直接可以看出来)
的卷积核,灰色地带表示卷积后的感受野(后面有相关计算公式,这里都是一层卷积的,直接可以看出来)a是普通的卷积过程(dilation rate = 1),卷积后的感受野为3 b是dilation rate = 2的空洞卷积,卷积后的感受野为5 c是dilation rate = 3的空洞卷积,卷积后的感受野为8
 ,卷积核的大小
,卷积核的大小  ,填充
,填充  ,步长
,步长  ,计算公式如下:
,计算公式如下:
dense prediction problems such as semantic segmentation ... to increase the performance of dense prediction architectures by aggregating multi-scale contextual information(来自[1])
三、感受野的计算

 的卷积,却可以起到
的卷积,却可以起到  、
、  等卷积的效果,空洞卷积在不增加参数量的前提下(参数量=卷积核大小+偏置),却可以增大感受野,假设空洞卷积的卷积核大小为
等卷积的效果,空洞卷积在不增加参数量的前提下(参数量=卷积核大小+偏置),却可以增大感受野,假设空洞卷积的卷积核大小为  ,空洞数为
,空洞数为  ,则其等效卷积核大小
,则其等效卷积核大小  ,例如
,例如  的卷积核,则
的卷积核,则  ,公式如下(来自[4])
,公式如下(来自[4])
当前层的感受野计算公式如下,其中,
 表示当前层的感受野,
表示当前层的感受野,  表示上一层的感受野,
表示上一层的感受野,  表示卷积核的大小
表示卷积核的大小
 表示之前所有层的步长的乘积(不包括本层),公式如下:
表示之前所有层的步长的乘积(不包括本层),公式如下:









四、潜在的问题及解决方法
Panqu Wang,Pengfei Chen, et al**.Understanding Convolution for Semantic Segmentation.//**WACV 2018 Fisher Yu, et al. Dilated Residual Networks. //CVPR 2017 Zhengyang Wang,et al.**Smoothed Dilated Convolutions for Improved Dense Prediction.//**KDD 2018. Liang-Chieh Chen,et al.Rethinking Atrous Convolution for Semantic Image Segmentation//2017 Sachin Mehta,et al. ESPNet: Efficient Spatial Pyramid of DilatedConvolutions for Semantic Segmentation. //ECCV 2018 Tianyi Wu**,et al.Tree-structured Kronecker Convolutional Networks for Semantic Segmentation.//AAAI2019** Hyojin Park,et al.Concentrated-Comprehensive Convolutionsfor lightweight semantic segmentation.//2018 Efficient Smoothing of Dilated Convolutions for Image Segmentation.//2019
下载1:何恺明顶会分享
在「AI算法与图像处理」公众号后台回复:何恺明,即可下载。总共有6份PDF,涉及 ResNet、Mask RCNN等经典工作的总结分析
下载2:leetcode 开源书
在「AI算法与图像处理」公众号后台回复:leetcode,即可下载。每题都 runtime beats 100% 的开源好书,你值得拥有!
下载3 CVPR2020 在「AI算法与图像处理」公众号后台回复:CVPR2020,即可下载1467篇CVPR 2020论文 个人微信(如果没有备注不拉群!) 请注明:地区+学校/企业+研究方向+昵称
觉得不错就点亮在看吧

评论

