引言

本着“凡我不能创造的，我就不能理解”的思想，本系列文章会基于纯Python以及NumPy从零创建自己的深度学习框架，该框架类似PyTorch能实现自动求导。

要深入理解深度学习，从零开始创建的经验非常重要，从自己可以理解的角度出发，尽量不适用外部完备的框架前提下，实现我们想要的模型。本系列文章的宗旨就是通过这样的过程，让大家切实掌握深度学习底层实现，而不是仅做一个调包侠。

上篇文章中，我们了解了线性回归。本文就来通过metagrad实现线性回归。

实现模型基类

class Module:
    '''
    所有模型的基类
    '''

    def parameters(self) -> List[Parameter]:
        parameters = []
        for name, value in inspect.getmembers(self):
            if isinstance(value, Parameter):
                parameters.append(value)
            elif isinstance(value, Module):
                parameters.extend(value.parameters())

        return parameters

    def zero_grad(self):
        for p in self.parameters():
            p.zero_grad()

    def __call__(self, *args, **kwargs):
        return self.forward(*args, **kwargs)

    def forward(self, *args, **kwargs) -> Tensor:
        raise NotImplementedError

类似PyTorch，我们也实现一个模型的基类，其中存放一些通用方法。代码如上。主要实现了梯度清零方法。

其中Parameter的定义如下：

class Parameter(Tensor):
    def __init__(self, data: Union[Arrayable, Tensor]) -> None:
        
        if isinstance(data, Tensor):
            data = data.data
        # Parameter都是需要计算梯度的
        super().__init__(data, requires_grad=True)

Parameter默认需要计算梯度，在Module的parameters()方法中利用Parameter类获取模型的所有参数。

实现线性回归

class Linear(Module):
    r"""
         对给定的输入进行线性变换: :math:`y=xA^T + b`

        Args:
            in_features: 每个输入样本的大小
            out_features: 每个输出样本的大小
            bias: 是否含有偏置，默认 ``True``
        Shape:
            - Input: `(*, H_in)` 其中 `*` 表示任意维度，包括none,这里 `H_{in} = in_features`
            - Output: :math:`(*, H_out)` 除了最后一个维度外，所有维度的形状都与输入相同，这里H_out = out_features`
        Attributes:
            weight: 可学习的权重，形状为 `(out_features, in_features)`.
            bias:   可学习的偏置，形状 `(out_features)`.
        """

    def __init__(self, in_features: int, out_features: int, bias: bool = True) -> None:
        self.in_features = in_features
        self.out_features = out_features

        self.weight = Parameter(Tensor.empty((out_features, in_features)))
        if bias:
            self.bias = Parameter(Tensor.zeros(out_features))
        else:
            self.bias = None
        self.reset_parameters()

    def reset_parameters(self) -> None:
        self.weight.assign(np.random.randn(self.out_features, self.in_features))

    def forward(self, input: Tensor) -> Tensor:
        x = input @ self.weight.T
        if self.bias is not None:
            x = x + self.bias

        return x

让我们的线性回归模型继承Module，同时定义权重和偏置大小。最后我们只需要实现前向传播算法，反向传播就交给我们的自动求导机制去完成。

这样，我们的线性回归模型就实现完成了。但为了我们的模型能够学习，我们需要定义损失函数。

实现损失基类

class _Loss(Module):
    '''
    损失的基类
    '''
    reduction: str  # none | mean | sum

    def __init__(self, reduction: str = "mean") -> None:
        self.reduction = reduction

参考了PyTorch，聚合方法支持均值和求和。

实现均方误差

class MSELoss(_Loss):
    def __init__(self, reduction: str = "mean") -> None:
        '''
        均方误差
        '''
        super().__init__(reduction)

    def forward(self, input: Tensor, target: Tensor) -> Tensor:
        assert input.size == target.size, f"Using a target size ({target.size}) that is different to the input size " \
                                           f"({input.size}). This will likely lead to incorrect results due to " \
                                           f"broadcasting. Please ensure they have the same size."

        errors = (input - target) ** 2
        if self.reduction == "mean":
            loss = errors.sum(keepdims=False) / len(input)
        elif self.reduction == "sum":
            loss = errors.sum(keepdims=False)
        else:
            loss = errors

        return loss

这里的input其实是模型的输出，target真实输出。

有了损失函数后，我们还需要优化方法来进行参数优化。

实现优化方法

class Optimizer:
    def __init__(self, params: List[Parameter]) -> None:
        self.params = params

    def zero_grad(self) -> None:
        for p in self.params:
            p.zero_grad()

    def step(self) -> None:
        raise NotImplementedError

我们如上实现了优化方法的基类。下面就是实现随机梯度下降法(SGD)。

实现随机梯度下降法

class SGD(Optimizer):
    '''
    随机梯度下降
    '''

    def __init__(self, params: List[Parameter], lr: float = 1e-3) -> None:
        super().__init__(params)
        self.lr = lr

    def step(self) -> None:
        for p in self.params:
            p -= p.grad * self.lr

lr是学习率，每次调用step()都会进行参数更新。

线性回归实例

我们基于上篇文章中采集的深圳市南山区临近地铁口二手房价的数据为例：

# 面积
areas = [64.4, 68, 74.1, 74., 76.9, 78.1, 78.6]
# 挂牌售价
prices = [6.1, 6.25, 7.8, 6.66, 7.82, 7.14, 8.02]

我们先考虑面积和挂牌价(可能是指导价  单位：万/㎡)之间的关系。

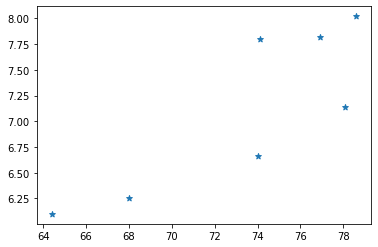
看上去似乎有一定的线性关系。我们这里简单的考虑套内面积，实际上我们买房时还会考虑房龄、离地铁口距离、小区周边环境、空气质量、小区绿化区面积等。

这里我们尝试通过画一条直线，使得该直线尽可能和每个样本的距离最短。

# !pip install git+https://github.com/nlp-greyfoss/metagrad.git --upgrade
from metagrad.loss import MSELoss
from metagrad.module import Linear
from metagrad.optim import SGD
from metagrad.tensor import Tensor

model = Linear(1, 1)

optimizer = SGD(model.parameters(), lr=1e-1)

loss = MSELoss()

# 面积
areas = [64.4, 68, 74.1, 74., 76.9, 78.1, 78.6]
# 挂牌售价
prices = [6.1, 6.25, 7.8, 6.66, 7.82, 7.14, 8.02]

X = Tensor(areas).reshape((-1, 1))
y = Tensor(prices).reshape((-1, 1))

epochs = 100
losses = []
for epoch in range(epochs):
  l = loss(model(X), y)
  optimizer.zero_grad()
  l.backward()
  optimizer.step()
  epoch_loss = l.data
  
  losses.append(epoch_loss)

  print(f'epoch {epoch + 1}, loss {float(epoch_loss):f}')

上面就是通过我们自己的metagrad实现的线性回归学习过程，是不是看上去有那味了。

输出：

epoch 1, loss 198.071304
epoch 2, loss 232059248.000000
epoch 3, loss 272126879727616.000000
epoch 4, loss 319112649512125988864.000000
epoch 5, loss 374211056107641585692311552.000000
epoch 6, loss 438822818730812850430760481456128.000000
epoch 7, loss inf
...

怎么损失不降反增了!?

莫慌，我们只有一个变量，不存在两个变量的量纲不同的问题。此时，该显示一下我们AI调参师的技术了。

损失太大，可能是梯度太大了，我们直接将学习率调小。

optimizer = SGD(model.parameters(), lr=1e-4)

我们修改学习率为1e-4：

epoch 1, loss 21798.214844
epoch 2, loss 153.602646
epoch 3, loss 1.260477
epoch 4, loss 0.188241
epoch 5, loss 0.180694
epoch 6, loss 0.180641
epoch 7, loss 0.180641
epoch 8, loss 0.180641
epoch 9, loss 0.180641
epoch 10, loss 0.180641
epoch 11, loss 0.180641
epoch 12, loss 0.180640
...
epoch 99, loss 0.180638
epoch 100, loss 0.180638

从输出可以看出，第4次迭代后，损失就一直不变了，我们看一下学习率曲线：

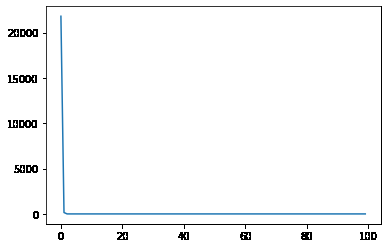
我们可以打印出得到的参数：

> w, b = model.weight.data.item(),model.bias.data.item()
> print(f'w: {w}, b:{b}')
w: 0.09660441144108287, b:0.026999891111711846

然后画出线性回归拟合的直线：

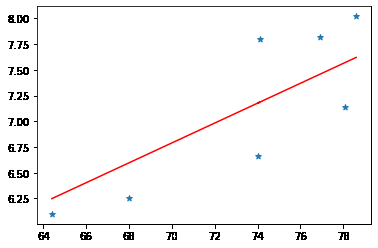
看上去还可以，如果你要买房的话，建议你买直线下面的房子。

基于我们这点训练样本，得到最后的损失为，我们能否使它再次降低呢？

一种方法是收集更多的数据，另一种方法是利用所有的维度。我们还有一个房龄维度没有利用。下面把它加进来。

# 面积
> areas = [64.4, 68, 74.1, 74., 76.9, 78.1, 78.6]
# 房龄
> ages = [31, 21, 19, 24, 17, 16, 17]
> X = np.stack([areas, ages]).T
> print(X)
array([[64.4, 31. ],
       [68. , 21. ],
       [74.1, 19. ],
       [74. , 24. ],
       [76.9, 17. ],
       [78.1, 16. ],
       [78.6, 17. ]])

第1列是面积，第2列是房龄，每行数据代表一个样本。

下面我们改写上面的线性回归代码，再次训练一个线性回归模型：

model = Linear(2, 1) # in_features: 2  out_features: 1

optimizer = SGD(model.parameters(), lr=1e-4)

loss = MSELoss()

# 面积
areas = [64.4, 68, 74.1, 74., 76.9, 78.1, 78.6]
# 房龄
ages = [31, 21, 19, 24, 17, 16, 17]

X = np.stack([areas, ages]).T
# 挂牌售价
prices = [6.1, 6.25, 7.8, 6.66, 7.82, 7.14, 8.02]


X = Tensor(X)
y = Tensor(prices).reshape((-1, 1))

epochs = 1000
losses = []
for epoch in range(epochs):
  l = loss(model(X), y)
  optimizer.zero_grad()
  l.backward()
  optimizer.step()
  epoch_loss = l.data

  losses.append(epoch_loss)
  if (epoch+1) % 20 == 0:
    print(f'epoch {epoch + 1}, loss {float(epoch_loss):f}')

输出:

epoch 20, loss 10.742877
epoch 40, loss 8.136241
epoch 60, loss 6.171517
epoch 80, loss 4.690628
epoch 100, loss 3.574423
epoch 120, loss 2.733095
epoch 140, loss 2.098954
epoch 160, loss 1.620976
epoch 180, loss 1.260706
epoch 200, loss 0.989156
epoch 220, loss 0.784478
epoch 240, loss 0.630204
epoch 260, loss 0.513921
epoch 280, loss 0.426275
...
epoch 1000, loss 0.158022

加上房龄信息，最终可以使损失下降到。我们来看一下此时的权重和偏置：

> w, b = model.weight.data,model.bias.data.item()
> print(f'w: {w}, b:{b}')
w: [[ 0.10354146 -0.02362296]], b:-0.00232952055510911

可以看到，房龄特征对应的权重为，所以说房龄越大，房子的价值就越小，这一关系还是学到了的。

我们的训练集才7个样本，这真的是太少了，如果你收集更多的数据，一定可以获得更好的效果。

总结

本文我们通过metagrad实现了线性回归，以及一些基类方法。下篇文章我们就来学习逻辑回归。