用 SVD 分解直观地看最小二乘法
下面这篇揭示了矩阵的基本子空间理论可以很好地解释降维算法的原理。
从奇异值分解 SVD 看 PCA
实际上,子空间还可以拿来解释线性最小二乘法。我们用一个简单例子来直观地分析最小二乘问题及其解法。
1问题
假设我们要通过在弹簧上附加不同的重量并测量其长度来确定弹簧的弹性系数。
我们知道长度
其中,
假设我们已经进行了实验并获得了以下数据,
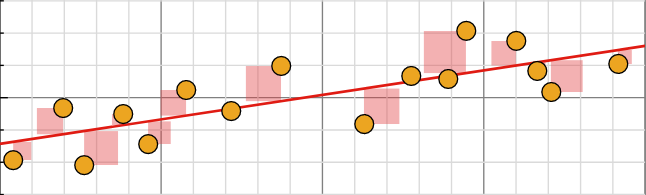
我们绘制了相应的散点图,显然这些点并不在一条直线上。这意味着我们不能精确地求得上面那两个待定常数。
由于测量中的误差不可避免,我们希望使用获得的所有数据以最大程度地减少误差的影响。因此引入了一个数据量超过未知数个数的线性方程组,即所谓的超定方程组,
或以矩阵形式写为,
我们将使用最小二乘法确定弹簧的弹性常数的近似值。
令
称为超定方程组:其方程式的个数多于未知数的个数。
2几何上直观来看
通常,上面这种方程组并没有解。例如,当
我们在
如下图所示,可以看到这样的问题通常并不能找到解。两个向量
在这种情况下,求解线性方程组的一个明显替代方案是使如下向量,
尽可能地小。
这里,
在最小二乘法中,我们使用标准的欧几里得范数。因此,我们想找到使如下式子最小化的向量
由于未知向量
在该例子中,凭我们对
由于矩阵
可以写成如下矩阵形式,
然后,代入
求解上述方程组,可得解
3法方程
定理
假设
有唯一解。
证明
我们首先证明
等价于
然后,我们证明
可以将
于是有,
由于
证毕。
缺点
然而,用法方程解线性最小二乘问题有两个明显的缺点,
计算
可能导致信息丢失。 的条件数是 的条件数的平方,即
我们通过一个示例来说明第 1 点。
例子
给定
于是有,
假设
4使用 SVD 求解
最小二乘问题可以使用 SVD 来求解。假设我们有一个待定的线性方程组
矩阵
其中
其中,
现在,我们可以通过解
由于
所以解也可以写成,
下面将上述内容概括总结一下。
.基于 SVD 的最小二乘解
已知矩阵
然后最小二乘问题,
有如下唯一解,
.SVD 求解过程的几何解释
我们再次来看这个超定线性方程组,
结合下面这篇里的子空间理论,
求解上面方程组相当于要从矩阵
但是,这里的问题就出在向量
我们再来看一下解,
结合下图,我们把上式一步步来解读一下。
从右往左看,
但这个坐标并不是我们要的解,因为最终要的解是相对矩阵
现在来看黄色虚线向量,即
我们要找的是使下式成立的
把 SVD 分解
两边左乘
由于矩阵
.用线性变换来解释
我们知道,矩阵
现在,黄色虚向量
正向验证一下,坐标
.伪逆(广义逆矩阵)
我们再次看上面得到的解,
这里可以引出一个概念,那就是伪逆。
但是,要注意的是这里的矩阵不要求列满秩。
定义 矩阵
其中,
有了系数矩阵的伪逆,上面最小二乘问题的解是不是可以写得更简洁呢?
5收尾
本篇讲的是线性最小二乘问题,除了上面的解法还有很多其他方法,如求导、
另外,最小二乘有线性问题,自然也有非线性问题。那么所谓的非线性最小二乘问题会是怎么样呢?以及如何求解呢?这些问题后续展开。
