两种常见的周期性特征，时序必知强特

来源：kaggle竞赛宝典

在时间序列问题中，周期特征是异常重要的，例如：

• 地铁流量预测中的周期性，每周一到周五的早上地铁流量就特别大，但是到了周末人就比较少；
• 股票涨跌的预测问题中，在节假日之前，例如国庆等，白酒等的股价就会有提升；
• 在降雨量的预测中，每年的某些时节，降雨量就会大幅提升；
• 在电量预估问题中，因为夏天温度较高的原因，每年的夏天用电量会大幅提升；
• ......

上面这些在某些固定时间点周而复始的出现某种现象的，我们一般称之为周期性，那么在时间序列问题中，我们如何捕捉这些周期性呢？

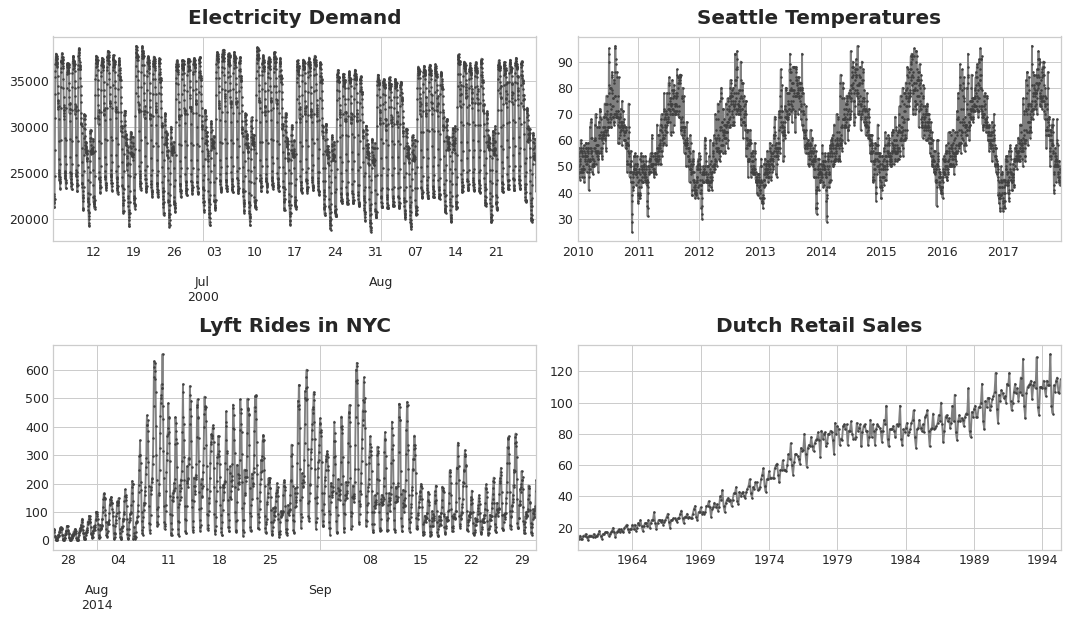
此处我们介绍两种常见的周期性特征。

1. 周期性indicators：适合于观测较少的情况，比如每周观测一次的周期；
2. 傅里叶特征：适合于存在许多观测的周期，比如每年每日观测周期；

时间周期特征

周期性indicators一般就是表示时间序列周期性的一些二元特征。例如每周一我们的数据呈现出某种周期性，我们会加入是否为周一来表示该信息，例如下表所示。

周期性indicators一般是我们有一些先验知识，但是还有一类数据，它的周期可能是每隔20天一次的周期，我们可以很容易的从图像中观测到，但是往往没法使用周期性indicators来捕捉此类信息。

此时我们可以使用傅里叶特征尝试捕捉此类到信息。

• 傅立叶特征就是一对正弦和余弦曲线，从最长的周期开始，每个潜在频率对应一对。傅里叶对建模年度周期性的频率：每年一次、每年两次、每年三次，依此类推。

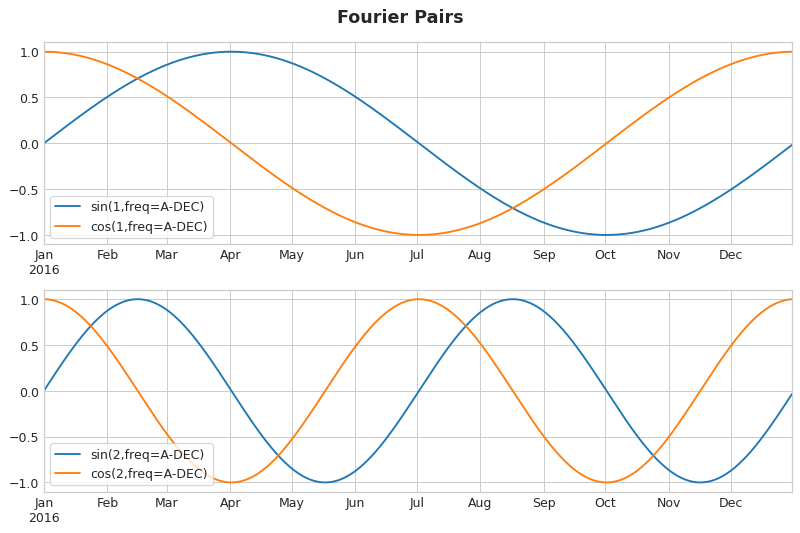
如果我们把这些sine和cosine的曲线加入到我们的训练集合中，往往可以取得不错的帮助，尤其是对于线性类的模型。

代码

• 代码摘自：https://www.kaggle.com/ryanholbrook/seasonality

import numpy as np


def fourier_features(index, freq, order):
    time = np.arange(len(index), dtype=np.float32)
    k = 2 * np.pi * (1 / freq) * time
    features = {}
    for i in range(1, order + 1):
        features.update({
            f"sin_{freq}_{i}": np.sin(i * k),
            f"cos_{freq}_{i}": np.cos(i * k),
        })
    return pd.DataFrame(features, index=index)


# Compute Fourier features to the 4th order (8 new features) for a
# series y with daily observations and annual seasonality:
#
# fourier_features(y, freq=365.25, order=4)

from statsmodels.tsa.deterministic import CalendarFourier, DeterministicProcess

fourier = CalendarFourier(freq="A", order=10)  # 10 sin/cos pairs for "A"nnual seasonality

dp = DeterministicProcess(
    index=tunnel.index,
    constant=True,               # dummy feature for bias (y-intercept)
    order=1,                     # trend (order 1 means linear)
    seasonal=True,               # weekly seasonality (indicators)
    additional_terms=[fourier],  # annual seasonality (fourier)
    drop=True,                   # drop terms to avoid collinearity
)

X = dp.in_sample()  # create features for dates in tunnel.index

适用问题

如果可视化分析中发现数据存在周期性的话，就可以使用上面的两种策略进行周期性特征的抽取。

参考文献

1. Seasonality