今天去洗车,我居然发现CPU的···
有趣的问题
前几天摸鱼的时候,我在stackoverflow发现一个有趣的问题:
https://stackoverflow.com/questions/11227809/why-is-processing-a-sorted-array-faster-than-processing-an-unsorted-array
提问者用C++写了一个数组求和的函数,把数组排序后求和和无序求和的计算性能竟然相差6倍,十分诡异。
我们来看下代码:
#include
#include
#include
int main()
{
// Generate data
const unsigned arraySize = 32768;
int data[arraySize];
for (unsigned c = 0; c < arraySize; ++c)
data[c] = std::rand() % 256;
// !!! With this, the next loop runs faster.
std::sort(data, data + arraySize);
// Test
clock_t start = clock();
long long sum = 0;
for (unsigned i = 0; i < 100000; ++i)
{
for (unsigned c = 0; c < arraySize; ++c)
{ // Primary loop
if (data[c] >= 128)
sum += data[c];
}
}
double elapsedTime = static_cast(clock()-start) / CLOCKS_PER_SEC;
std::cout << elapsedTime << '\n';
std::cout << "sum = " << sum << '\n';
代码比较简单,先搞了个大数组,然后数组的元素是256以内取模,所有元素都落在0-256之内,接着在循环里面使用条件判断求和。
提问者为了防止有单次误差,做了10w次循环,发现运行时间差别很大:
无序求和 累计耗时 11.54秒 排序求和 累计耗时 1.93秒
对呀,按理说加了个std:sort()耗时会增加,但是性能还是这么优秀,真是奇怪呀!
提问者又用Java搞了一遍,现象和C++不能说一模一样,但几乎也是分毫不差。
究竟是咋回事呢?读到这里的盆友,一定是个技术人儿,来吧,让我们一探究竟。
洗车房的故事
前阵子我开着自己的捷达去洗车,车还挺多,排着队一个个搞。
我发现洗车流程是这样的:喷水、打泡沫、刷洗、擦拭、吹干。
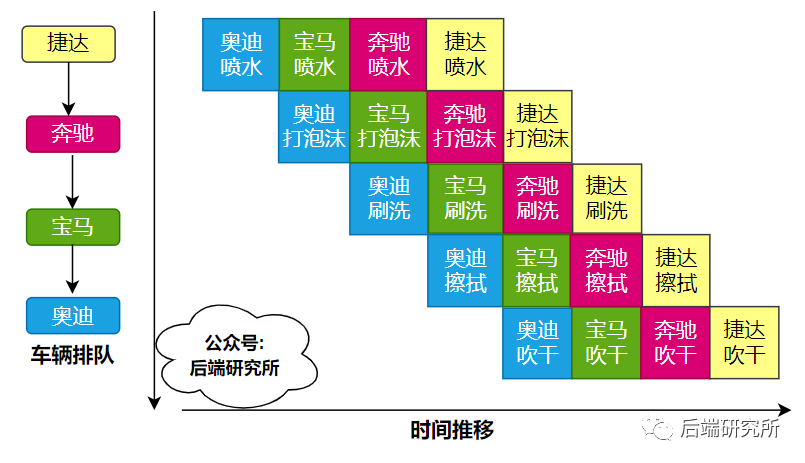
车辆在外面排队,依次是奥迪A6L、宝马X5、奔驰C200L、捷达vs5。
就这样一个工序完成后,车辆向下一个工序移动,当前工序又补进来一辆车。
我原来以为是一辆车进去 完成所有工序再出来,下一辆进行完成全部工序,依次类推,没想到洗车房还是流水线作业。
为啥是流水线呢?提高洗车数量,也就是吞吐量,单位时间赚取更多噻!
如果是完成所有工序再搞下一辆,这样某个时刻5个工序只有1个在做,其他4共工序都是等待状态,工人们都开始摸鱼了,钱也没赚到,客户等待时间还长。
生活中的智慧还真是不少呀,看到这里不禁要问,这和前面的数组求和有啥关系呢?别急,还真有关系。
CPU的内部的那些事儿
我们先从一个宏观角度去看下CPU内部的结构:
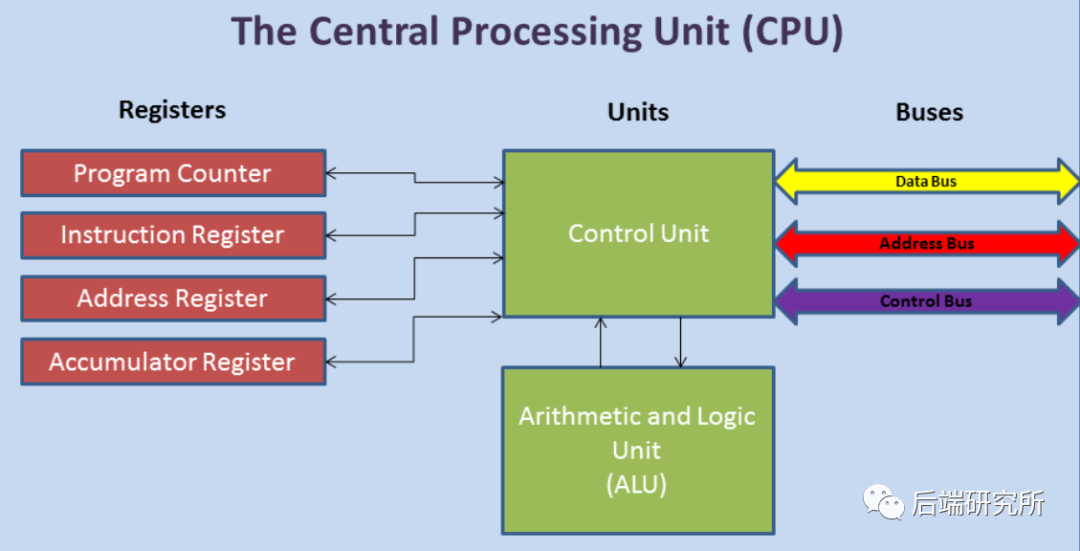
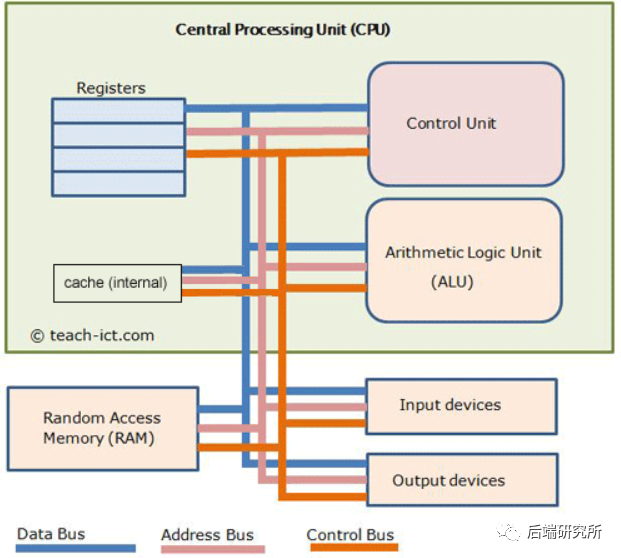
从两个图上,我们可以得到如下信息:
CPU内部的核心组件有各类寄存器、控制单元CU、逻辑运算单元ALU、高速缓存 CPU和外部交互的交通大动脉就是三种总线:地址总线、数据总线、控制总线 I/O设备、RAM通过三大总线和CPU实现功能交互
程序经过编译器处理成机器码来执行,程序会被翻译成一条条的指令,为了简化问题,我们选择5级流水线的CPU来说明问题:
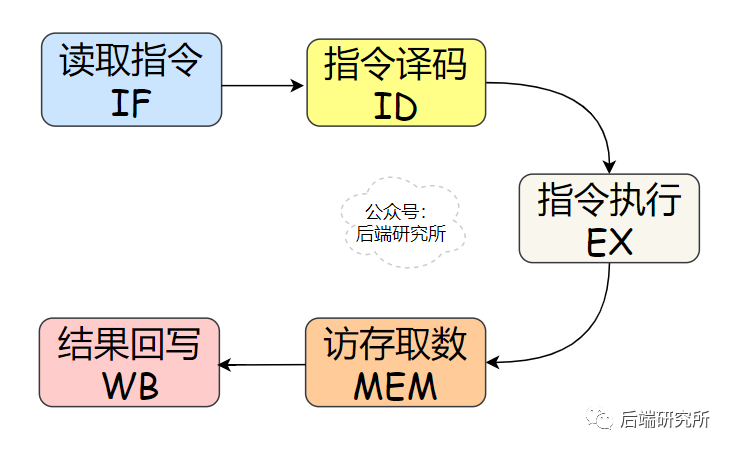
取指令IF
取指令(Instruction Fetch,IF)阶段是将一条指令从主存中取到指令寄存器的过程。指令译码ID
取出指令后,计算机立即进入指令译码(Instruction Decode,ID)阶段。
在指令译码阶段,指令译码器按照预定的指令格式,对取回的指令进行拆分和解释,识别区分出不同的指令类别以及各种获取操作数的方法。指令执行EX
在取指令和指令译码阶段之后,接着进入执行指令(Execute,EX)阶段。
此阶段的任务是完成指令所规定的各种操作,具体实现指令的功能。为此,CPU的不同部分被连接起来,以执行所需的操作。访存取数阶段MEM
根据指令需要,有可能要访问主存读取操作数,这样就进入了访存取数(Memory,MEM)阶段,此阶段的任务是:根据指令地址码,得到操作数在主存中的地址,并从主存中读取该操作数用于运算。结果回写WB
作为最后一个阶段,结果写回(Writeback,WB)阶段把执行指令阶段的运行结果数据写回到某种存储形式。
上面的IF、ID、EX、MEM、WB就是CPU的5级流水线,这个流程和洗车房的流水线很相似:
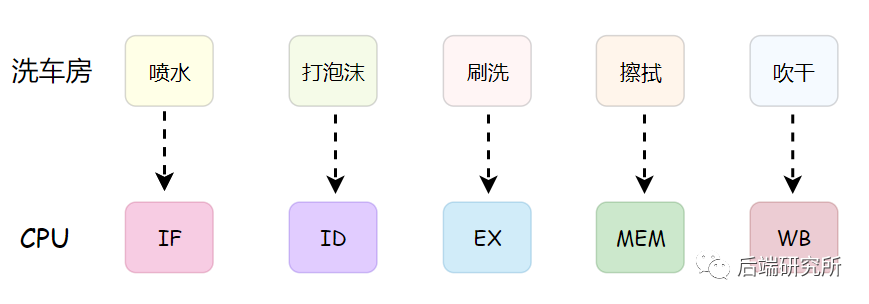
没错,CPU内部处理一条条指令的过程和洗车房就非常相似,我们继续深挖!
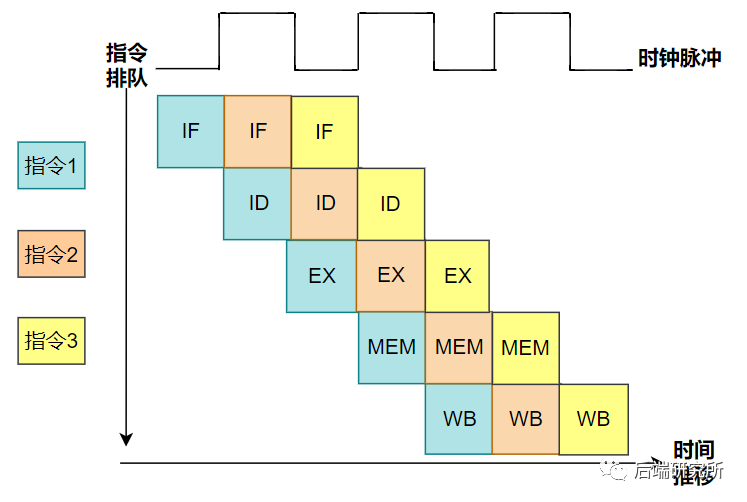
小结:CPU流水线技术是一种将指令分解为多步,并让不同指令的各步操作重叠,从而实现几条指令并行处理,以加速程序运行过程的技术。
指令的每步有各自独立的电路来处理,每完成一步,就进到下一步,而前一步则处理后续指令,属于CPU硬件电路层面的并发。
CPU流水线吞吐量和延迟
我们来看下引入流水线之后吞吐量的变化: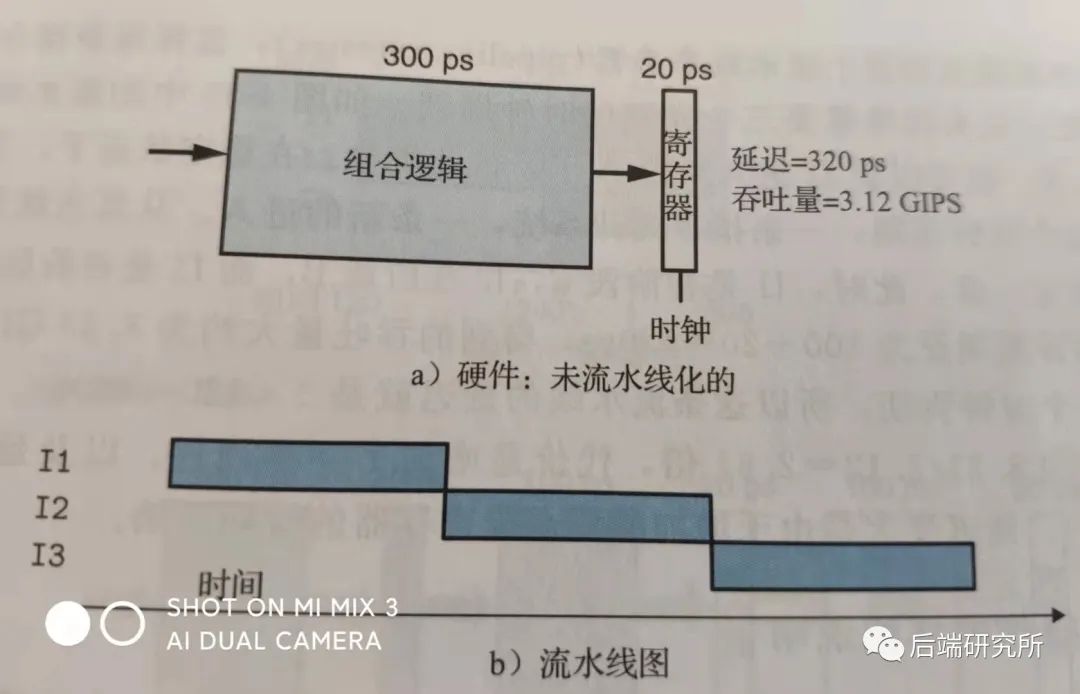 未使用流水线时各个执行部分组成了组合逻辑,执行完成后写寄存器,整个时间包括:组合逻辑时间300ps和写寄存器20ps,这就类似于洗车房每次5个工序一起搞定一辆车的情况。
未使用流水线时各个执行部分组成了组合逻辑,执行完成后写寄存器,整个时间包括:组合逻辑时间300ps和写寄存器20ps,这就类似于洗车房每次5个工序一起搞定一辆车的情况。
该模式下的吞吐量是1/(300+20)ps = 3.125GIPS(每秒千兆条指令)
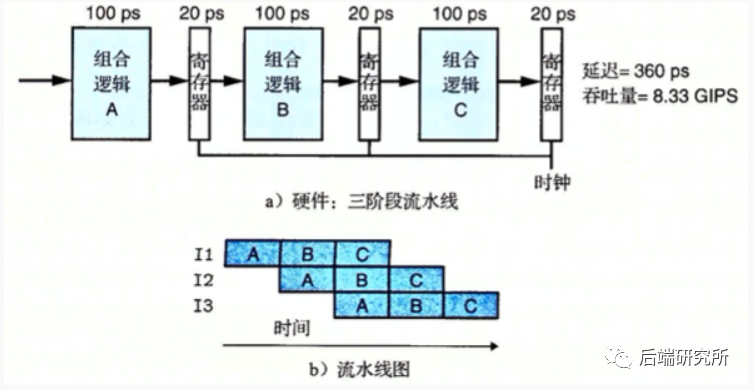
使用流水线时,组合逻辑被拆分为3个部分,但是每个部分都需要写寄存器,这样就增加了整个流程的时间从320ps提高到了360ps。
拆分多出两个逻辑和两个寄存器写,额外多出40ps。
此时的吞吐量是1/(100+20)ps = 8.333GIPS(每秒千兆条指令),整个吞吐量是未使用流水线的2.67倍。
从上面的对比来看,增加了一些硬件和延迟带来了吞吐量的提升,但是一味增加硬件不是万金油,单纯的写寄存器延迟就很明显。
流水线的级数也被称为深度,当前intel的酷睿i7采用了16级深度的流水线,在一定范围内提高流水线深度可以提高CPU的吞吐量,但是也为硬件设计带来很大的挑战,甚至降低吞吐量。
CPU流水线冒险
通过流水线设计来提升 CPU 的吞吐率,是一把双刃剑,在提高吞吐量的同时我们也在冒险。
所谓的冒险就是一帆风顺路上的磕磕绊绊,坑坑洼洼,流水线也并非一帆风顺的。
提到流水线设计需要解决的三大冒险:结构冒险(Structural Hazard)、数据冒险(Data Hazard)以及控制冒险(Control Hazard)。
结构冒险
结构冒险本质上是一种硬件冲突,我们以5级流水线为例来说,指令读取IF阶段和取数操作MEM,都需要进行内存数据的读取,然而内存只有一个地址译码器,只能在一个时钟周期里面读取一条数据。
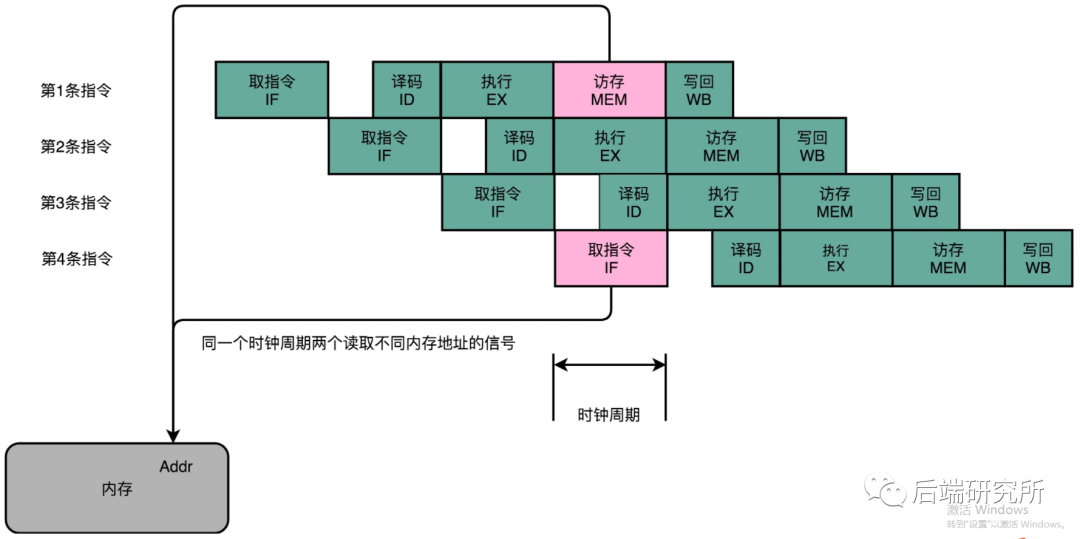
换句话说就像洗车流水线的喷水和刷洗都要用到水管,但是只有一根水管,这样就存在冲突,导致只能满足一个喷水或者刷洗。
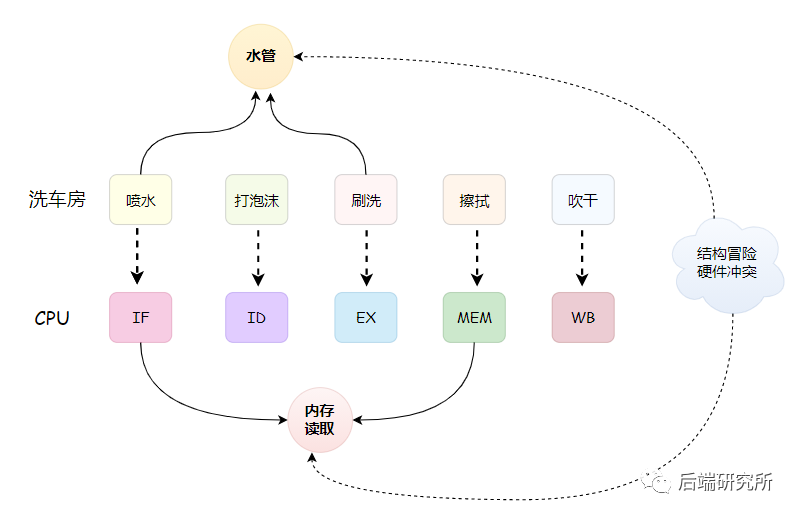
对于MEM阶段和IF阶段的冲突,一个解决方案就是把内存分成两部分:存放指令的内存和存放数据的内存,让它们有各自的地址译码器,从而通过增加硬件资源来解决冲突。
没错,这种将指令和数据分开存储就是著名的哈佛结构Harvard Architecture,指令和数据放在一起的就是冯诺依曼结构/普林斯顿结构Princeton Architecture。
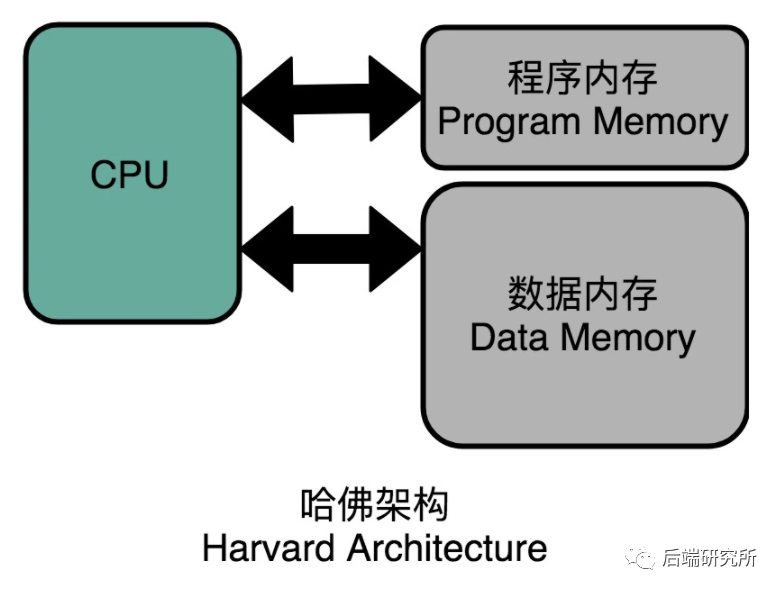
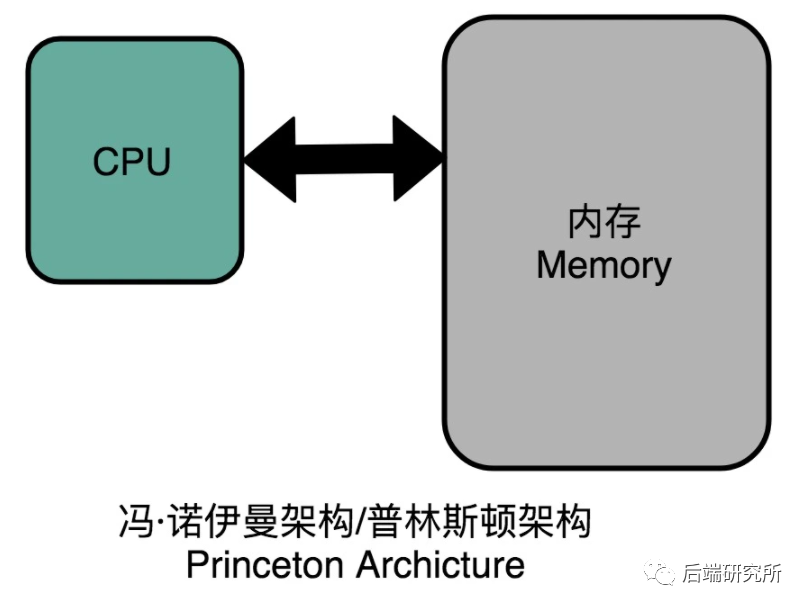
这两种结构有各自优缺点,现代CPU借鉴了两种架构采用一种混合结构,并且引入高速缓存,来降低CPU和内存的速度不匹配问题,如图:
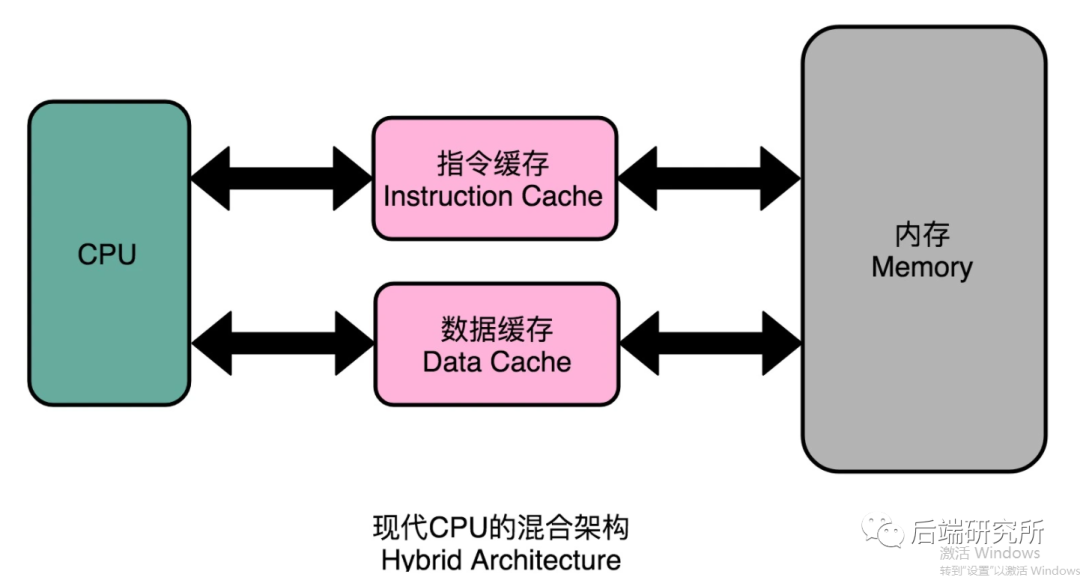
这种混合结构就很好地解决了流水线结构冒险问题,只是硬件结构更复杂了,属于硬件层面的优化。
数据冒险
数据冒险是指令之间存在数据依赖关系,就像这段代码:
int a = 10;
int b = a + 10;//语句2
int c = b + a;//语句3
语句3的计算依赖于b的值,在语句2对b进行了计算,也就是语句3依赖于语句2,但是每一个语句都会被翻译成很多的指令,也就是其中两个指令存在依赖关系。
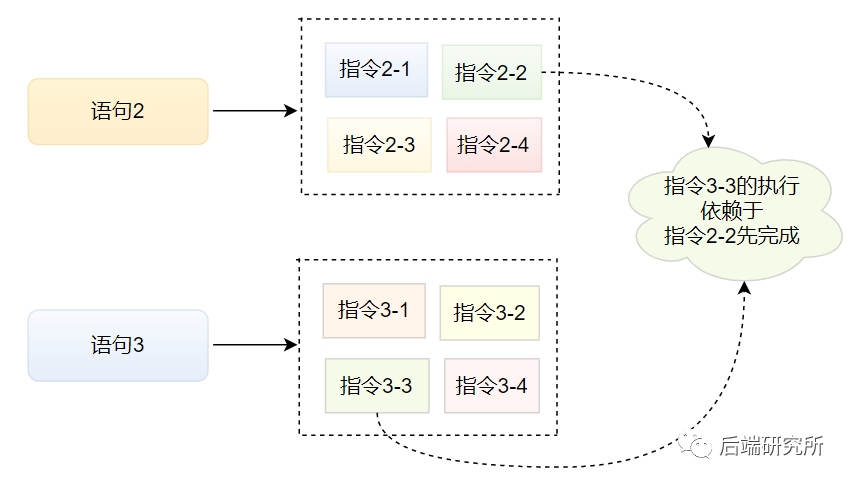
比如说指令3-3需要等待指令2-2完成WB阶段才可以进行EX阶段,如果不等待得到的结果就是错误的。
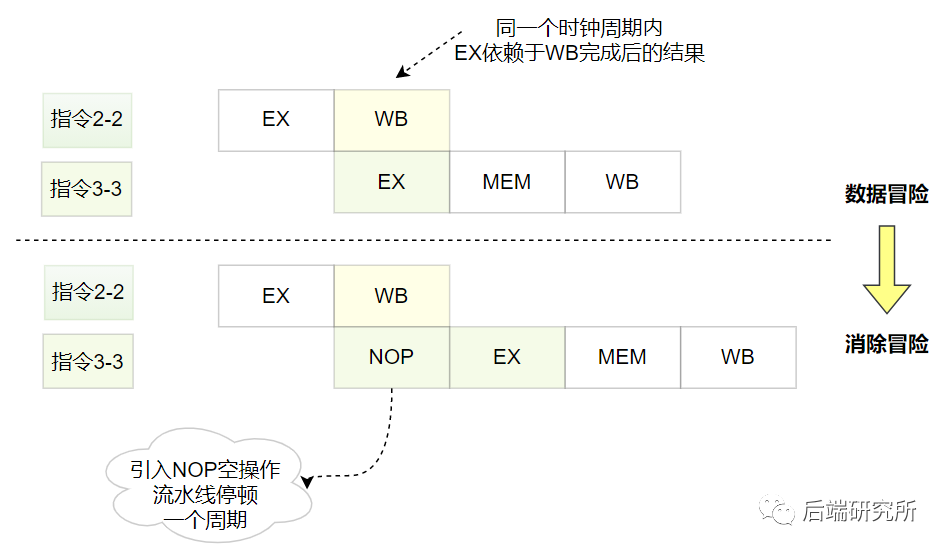
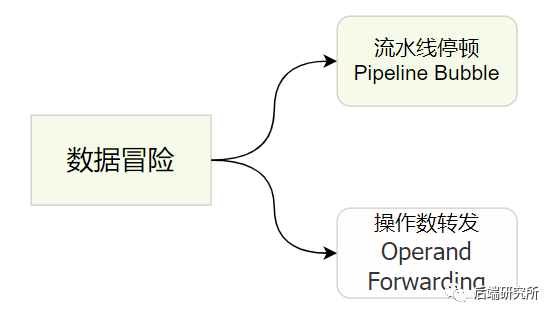
一种解决方案就是引入NOP操作,这个时钟周期啥也不做,等到依赖的数据完成再继续,这种通过流水线停顿解决数据冒险的方案称为流水线冒泡(Pipeline Bubble)。
流水线冒泡虽然简单,但是效率却下降了,经过大量的实践发现,我们完全可以在第一条指令的结果数据传输给到下一条指令的 ALU,下一条指令不需要再插入NOP 阶段,就可以继续正常进行了。
这种将结果直接传输的技术称为操作数前推/转发Operand Forwarding,它可以和流水线冒泡NOP一起使用,因为单纯的操作数前推也无法完全避免使用NOP。
小结:操作数前推,就是通过在硬件层面制造一条旁路,让一条指令的计算结果,可以直接传输给下一条指令,而不再需要指令 1 写回寄存器,指令 2 再读取寄存器,这样多此一举的操作。
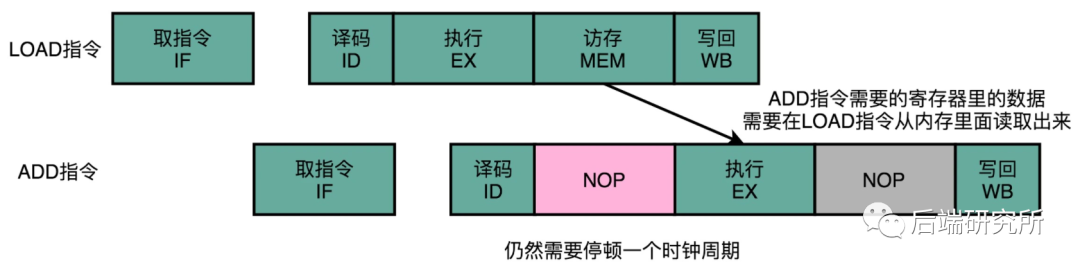 ADD指令不需要等待WB完成再执行EX,而是LOAD指令通过操作数转发直接传给ADD指令,减少了一个NOP操作,只需要1个NOP操作即可,提升了流水线效率。
ADD指令不需要等待WB完成再执行EX,而是LOAD指令通过操作数转发直接传给ADD指令,减少了一个NOP操作,只需要1个NOP操作即可,提升了流水线效率。
控制冒险
在流水线中,多个指令是并行执行的,在指令1执行的时候,后续的指令2和指令3可能已经完成了IF和ID两个阶段等待被执行,此时如果指令1一下子跳到了其他地方,那么指令2和指令3的IF和ID就是无用功了。
遇到这种指令转移情况,处理器需要先排空指令2和指令3对应的流水线,然后跳转到指令1的新的目标位置进入新的流水线,这部分称为转移开销,这也是产生性能损失的重要原因。

转移指令本身和流水线的模式是冲突的,因为转移指令会改变指令的流向, 而流水线则希望能够依次地取回指令,将流水线填满的,但是转移指令在实际程序中非常普遍,这也是CPU流水线必须要面对的问题。
转移指令可以分为无条件转移和条件转移。
无条件转移是确定发生的,并且跳转地址在取指阶段就能得到,我们在 CPU 里面设计对应的旁路电路,把计算结果更早地反馈到流水线中,这种属于硬件方案称为缩短分支延迟。
但是,对于条件转移我们在IF阶段并不能获得跳转位置,只能等EX阶段才知道,这就引出了分支预测。

分支预测换句话说就是:流水线的上一个阶段还没有完成,但是下一个指令是啥要依赖于这个结果,为了效率,流水线不能停顿住,必须要做个选择,向左走还是 向右走,选择出下一条要执行的指令,哪怕错了,也比等待好,万一猜对了呢!
CPU分支预测
分支预测有:静态分支预测和动态分支预测。
静态分支预测就是每次都选择一个结果,就像抛硬币每次都猜正面,对于CPU流水线来说都猜指令不跳转,也就有50%的正确率了,这种预测方式简单但是不够高效。
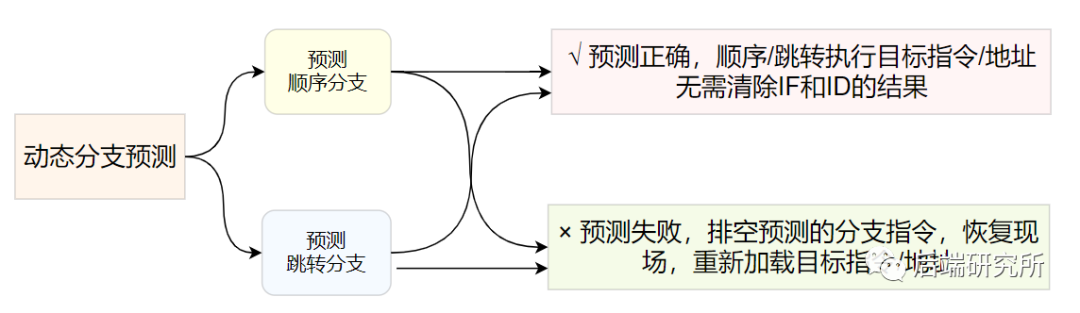
动态分支预测会根据之前的选择情况和正确率来预测当前的情况,做出判断是顺序分支还是跳转分支,因此仍然会有成功和失败两种情况。
比如分支预测选择了跳转分支之后:
预测成功时,尽快找到分支目标指令地址,避免控制相关造成流水线停顿。 预测错误时,要作废已经预取和分析的指令,恢复现场,并从另一条分支路径重新取指令。
最简单的动态分支预测器有1bit和2bit,其中2bit表示有2位标记,分别记录上一次预测状态和上次预测结果,讲到这里很多文章就一带而过,给了一个状态机迁移图,就草草收尾了:
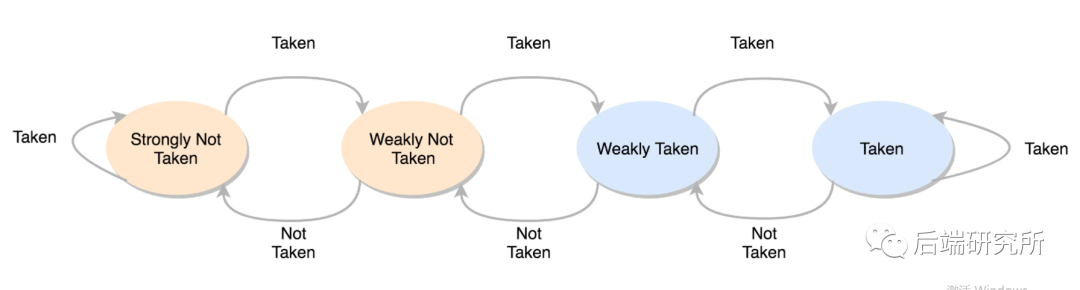
说实话,看到这图,我仿佛懂了,又仿佛没懂,于是我决定好好研究一下这个2bit分支预测器的一些原理,我们继续:
两种决策
not taken代表选择顺序分支
taken代表跳转分支四种状态
00 代表strongly not taken 强顺序分支
01 代表weakly not taken 弱顺序分支
10 代表weakly taken 弱跳转分支
11 代表strongly taken 强跳转分支
我们继续看2bit动态分支预测是如果进行状态机迁移的:
当前状态处于00 强顺序分支时
必然预测下一次也是顺序分支,此时会有两种结果,预测成功了,下一次状态仍然是00,预测失败了,最终程序选择了跳转分支,下一次状态变为01。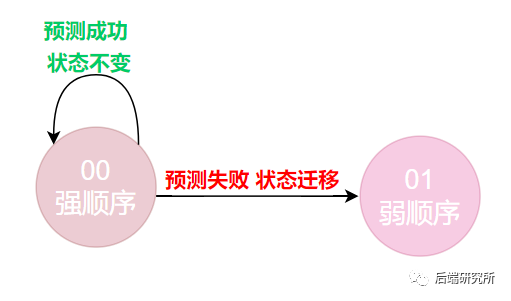
当前状态处于01 弱顺序分支时
必然预测下一次也是顺序分支,此时会有两种结果,预测成功了,下一次状态调整为00,预测失败了,最终程序选择了跳转分支,下一次状态变为10。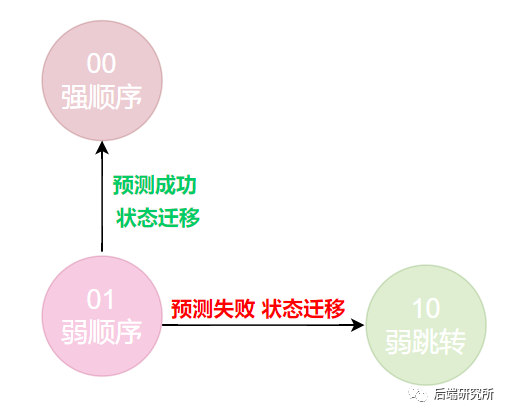
当前状态处于10 弱跳转分支时
必然预测下一次也是跳转分支,此时会有两种结果,预测成功了,下一次状态调整为11,预测失败了,最终程序选择了顺序分支,下一次状态变为01。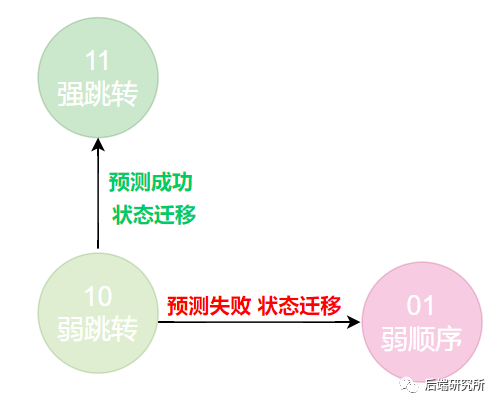
当前状态处于11 强跳转分支时
必然预测下一次也是跳转分支,此时会有两种结果,预测成功了,状态不变仍然是11,预测失败了,最终程序选择了顺序分支,下一次状态变为10。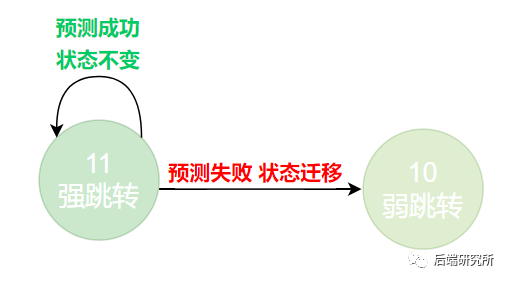
坚持看到这里,说明你真是个爱学习的人儿啊,我们来画一张完整的迁移图:
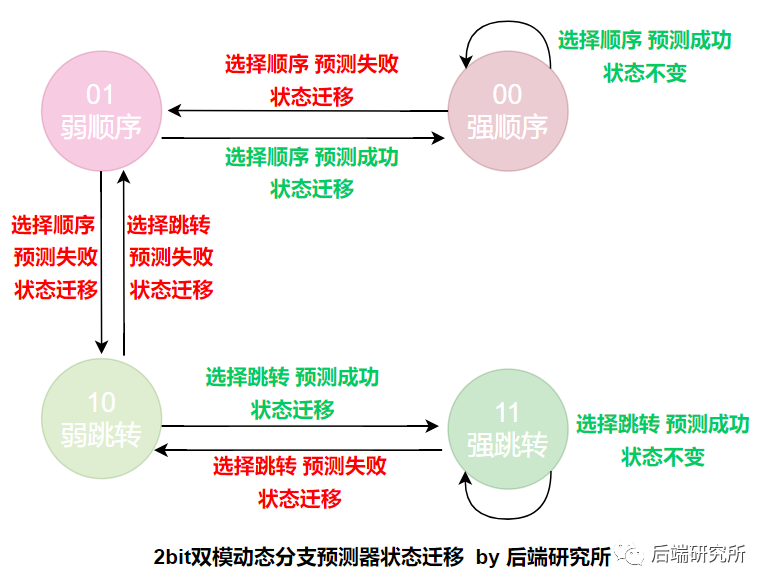
从这张图可以看到从顺序分支改变为跳转分支,需要连续两次预测失败,同样的跳转分支变为顺序分支,也需要连续两次预测失败:
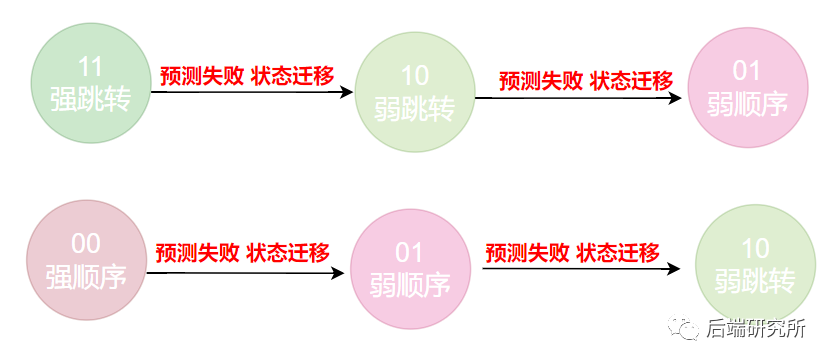
标记分支状态以及分支历史的一段内存被称为BTB,这段内存只存储了分支指令地址,以及预测的目标地址以及预测的位,这一块内容比较复杂,我们在此不展开了。
经过前面的分析可以看到动态分支预测器具有一定的容错性,并且波动性较小,只有连续两次预测失败才会转变选择结果,整体正确率提升明显。
从一些文章的数据显示,大部分情况下2bit预测器准确率可以达到95%以上: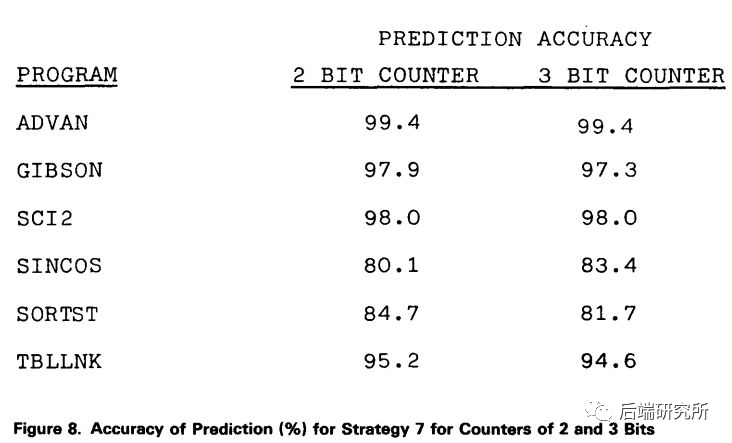
回顾问题
经过前面的一番分析,我们回到stackoverflow那个数组排序和无序耗时的问题上来,这个问题有两个关键因素:
数组元素是完全随机的,本次结果和上次结果是独立分布的 大量循环结构和条件判断的存在
没错,随机+循环+条件就彻底命中了CPU流水线的软肋。
数组排序之后的分支预测

数组未排序的分支预测

数组排序后,动态分支预测会结合之前的结果做出判断准确率非常高,未排序时完全随机和静态分支预测差不多了,因此准确率一般。
分支预测失败就意味着流水线排空,废弃已经进行IF和ID的指令,然后再选择正确的指令,整个过程在目前CPU来说要来浪费10-20个时钟周期,这样耗时就上来了。
总结
本文先从stackoverflow上一个关于随机数组排序和未排序求和的问题来切入。
进一步采用最简单的5级CPU流水线讲述基本原理和流水线中存在的三者冒险,及其各自的解决方法,特别是控制冒险。
进一步阐述了控制冒险中的分支预测技术,并展开了对双模动态分支预测器基本原理的剖析。
最后结合stackoverflow的问题,揭露流水线分支预测和随机数组排序/未排序在循环结构下的不同决策结果带来的巨大耗时影响。
本文先到这里,感谢朋友们的耐心阅读,我们下期见!
