第四章

4-1 生成3的乘方表 (15 分)

题目

输入一个非负整数n，生成一张3的乘方表，输出30~3n的值。可调用幂函数计算3的乘方。

输入格式:

❝

输入在一行中给出一个非负整数n。

输出格式:

❝

按照幂的递增顺序输出n+1行，每行格式为“pow(3,i) = 3的i次幂的值”。题目保证输出数据不超过长整型整数的范围。

输入样例:

❝

3

输出样例:

❝

pow(3,0) = 1

pow(3,1) = 3

pow(3,2) = 9

pow(3,3) = 27

解答

m = int(input())
for i in range(m+1):
    print("pow(3,{:d}) = {:d}".format(i, 3**i))

4-2 统计素数并求和 (20 分)

题目

本题要求统计给定整数_M_和_N_区间内素数的个数并对它们求和。

输入格式:

❝

输入在一行中给出两个正整数M和N（1≤M≤N≤500）。

输出格式:

❝

在一行中顺序输出M和N区间内素数的个数以及它们的和，数字间以空格分隔。

输入样例:

❝

10 31

输出样例:

❝

7 143

解答

def issu(num):
    if num == 1:
        return False
    for i in range(2, num):
        if num % i == 0:
            return False
    return True


m, n = map(int, input().split())
counts = 0
sum = 0
for i in range(m, n+1):
    if issu(i):
        counts += 1
        sum += i
print("{:d} {:d}".format(counts, sum))

4-3 猴子吃桃问题 (15 分)

题目

一只猴子第一天摘下若干个桃子，当即吃了一半，还不过瘾，又多吃了一个；第二天早上又将剩下的桃子吃掉一半，又多吃了一个。以后每天早上都吃了前一天剩下的一半加一个。到第N天早上想再吃时，见只剩下一个桃子了。问：第一天共摘了多少个桃子？

输入格式:

❝

输入在一行中给出正整数N（1<N≤10）。

输出格式:

❝

在一行中输出第一天共摘了多少个桃子。

输入样例:

❝

3

输出样例:

❝

10

解答

m = int(input())
ans = 1
for i in range(1, m):
    ans = (ans + 1) * 2
print(ans)

4-4 验证“哥德巴赫猜想” (20 分)

题目

数学领域著名的“哥德巴赫猜想”的大致意思是：任何一个大于2的偶数总能表示为两个素数之和。比如：24=5+19，其中5和19都是素数。本实验的任务是设计一个程序，验证20亿以内的偶数都可以分解成两个素数之和。

输入格式：

❝

输入在一行中给出一个(2, 2 000 000 000]范围内的偶数N。

输出格式：

❝

在一行中按照格式“N = p + q”输出N的素数分解，其中p ≤ q均为素数。又因为这样的分解不唯一（例如24还可以分解为7+17），要求必须输出所有解中p最小的解。

输入样例：

❝

24

输出样例：

❝

24 = 5 + 19

解答

提交代码 - 1

import math


def issu(num):
    for i in range(2, int(math.sqrt(num))+1):
        if num % i == 0:
            return False
    return True


m = int(input())
for i in range(2, m):
    if issu(i) and issu(m-i):
        print("{} = {} + {}".format(m, i, m-i))
        break

提交代码 - 2

import math


def issu(num):
    for i in range(2, int(math.sqrt(num))+1):
        if num % i == 0:
            return False
    return True


m = int(input())
for i in range(2, m//2+1):
    if issu(i) and issu(m-i):
        print("{} = {} + {}".format(m, i, m-i))
        break

4-5 求e的近似值 (15 分)

题目

自然常数 e 可以用级数 1+1/1!+1/2!+⋯+1/n!+⋯ 来近似计算。本题要求对给定的非负整数 n，求该级数的前 n+1 项和。

输入格式:

❝

输入第一行中给出非负整数 n（≤1000）。

输出格式:

❝

在一行中输出部分和的值，保留小数点后八位。

输入样例:

❝

10

输出样例:

❝

2.71828180

解答

提交代码 - 1

def factorial(num):
    ans = 1
    for i in range(1, num+1):
        ans *= i
    return ans


N = int(input())
sum = 1
for i in range(1, N+1):
    sum += 1/factorial(i)
print("{:.8f}".format(sum))

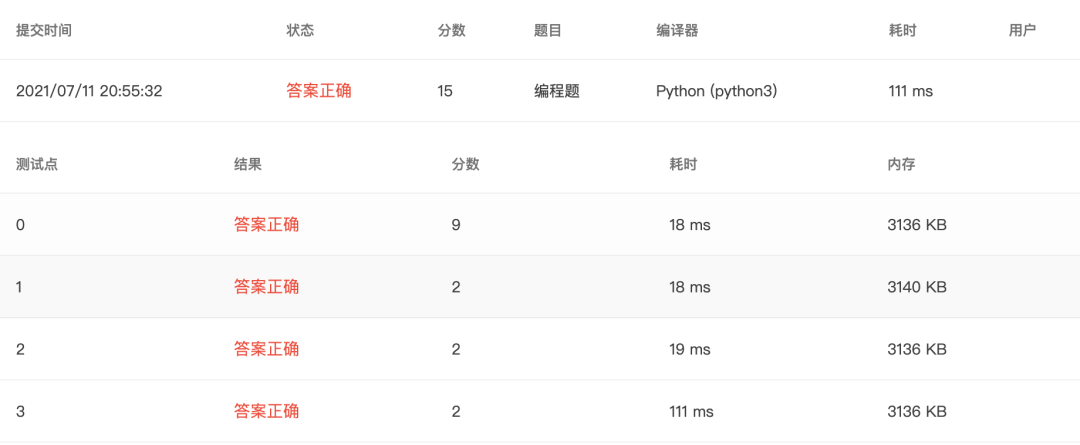
提交代码 - 2

N = int(input())
num = 1
sum = 1
for i in range(1, N+1):
    num *= i
    sum += 1/num
print("{:.8f}".format(sum))

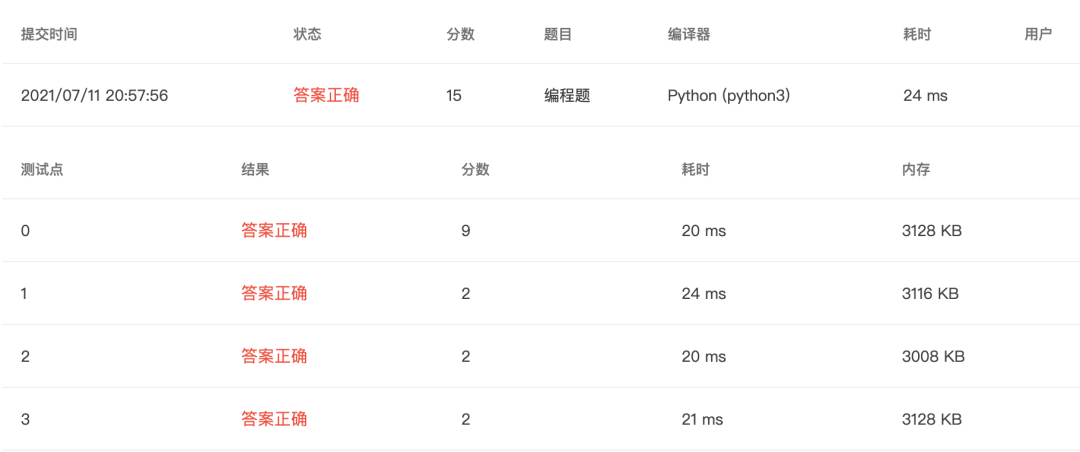
4-6 输出前 n 个Fibonacci数 (15 分)

题目

本题要求编写程序，输出菲波那契（Fibonacci）数列的前_N_项，每行输出5个，题目保证输出结果在长整型范围内。Fibonacci数列就是满足任一项数字是前两项的和（最开始两项均定义为1）的数列，例如：1，1，2，3，5，8，13，...。

输入格式:

❝

输入在一行中给出一个整数N（1≤N≤46）。

输出格式:

❝

输出前N个Fibonacci数，每个数占11位，每行输出5个。如果最后一行输出的个数不到5个，也需要换行。如果N小于1，则输出"Invalid."

输入样例1:

❝

7

输出样例1:

❝

      1          1          2          3          5           8         13

输入样例2：

❝

0

输出样例2：

❝

Invalid.

解答

n = int(input())
if n < 1:
    print("Invalid.")
a = 0
b = 1
c = 1
count = 0
for i in range(n):
    print("{:>11d}".format(c), end="")
    c = a + b
    a = b
    b = c
    count += 1
    if count == 5 or i == n-1:
        print("\n", end="")
        count = 0

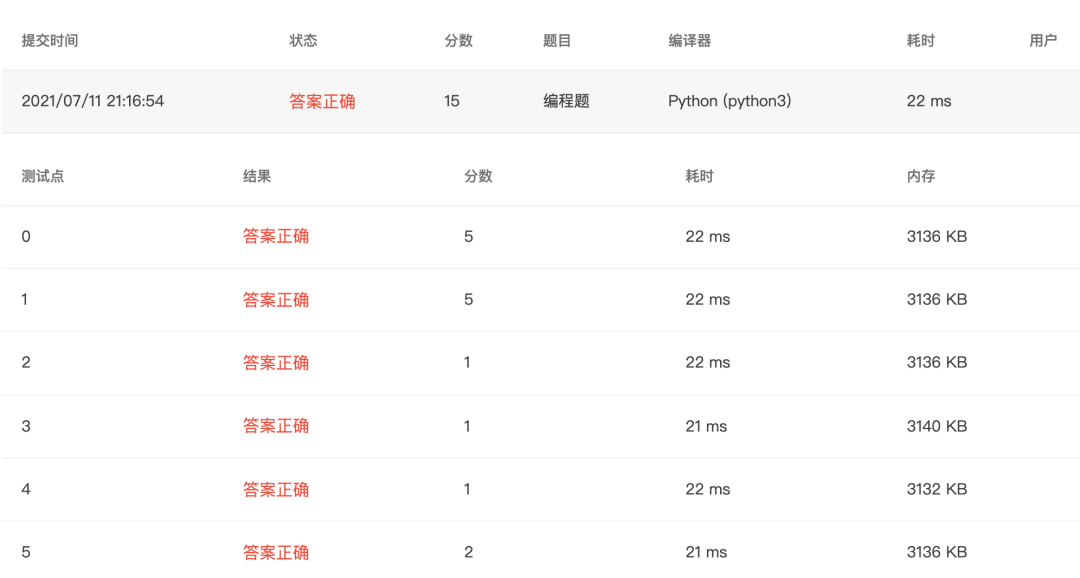
4-7 统计学生平均成绩与及格人数 (15 分)

题目

本题要求编写程序，计算学生们的平均成绩，并统计及格（成绩不低于60分）的人数。题目保证输入与输出均在整型范围内。

输入格式:

❝

输入在第一行中给出非负整数N，即学生人数。第二行给出N个非负整数，即这N位学生的成绩，其间以空格分隔。

输出格式: 按照以下格式输出：

❝

average = 成绩均值 count = 及格人数

其中平均值精确到小数点后一位。

输入样例:

❝

5 77 54 92 73 60

输出样例:

❝

average = 71.2 count = 4

解答

nums = int(input())
if(nums == 0):
    print('average = 0.0')
    print('count = 0')
    exit()
grades = list(map(int, input().split()))
average = 0
count = 0
for i in grades:
    average += i
    if i >= 60:
        count += 1
print("average = {:.1f}".format(average/nums))
print("count = {:d}".format(count))

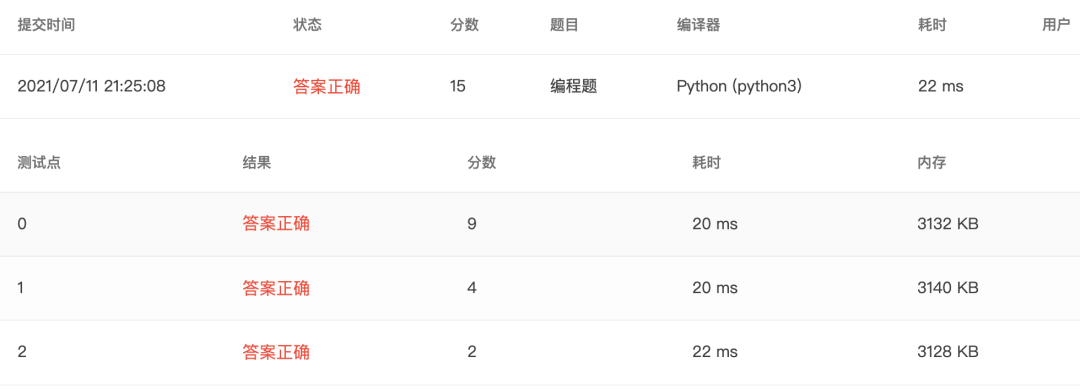
4-8 求分数序列前N项和 (15 分)

题目

本题要求编写程序，计算序列 2/1+3/2+5/3+8/5+... 的前N项之和。注意该序列从第2项起，每一项的分子是前一项分子与分母的和，分母是前一项的分子。

本题要求编写程序，计算序列 2/1+3/2+5/3+8/5+... 的前N项之和。注意该序列从第2项起，每一项的分子是前一项分子与分母的和，分母是前一项的分子。

输入格式:

❝

输入在一行中给出一个正整数N。

输出格式:

❝

在一行中输出部分和的值，精确到小数点后两位。题目保证计算结果不超过双精度范围。

输入样例:

❝

20

输出样例:

❝

32.66

解答

提交代码 - 1

n = int(input())
a = 2
b = 1
sum = 2
for i in range(n-1):
    t = a
    a = a + b
    b = t
    sum += a/b
print("{:.2f}".format(sum))

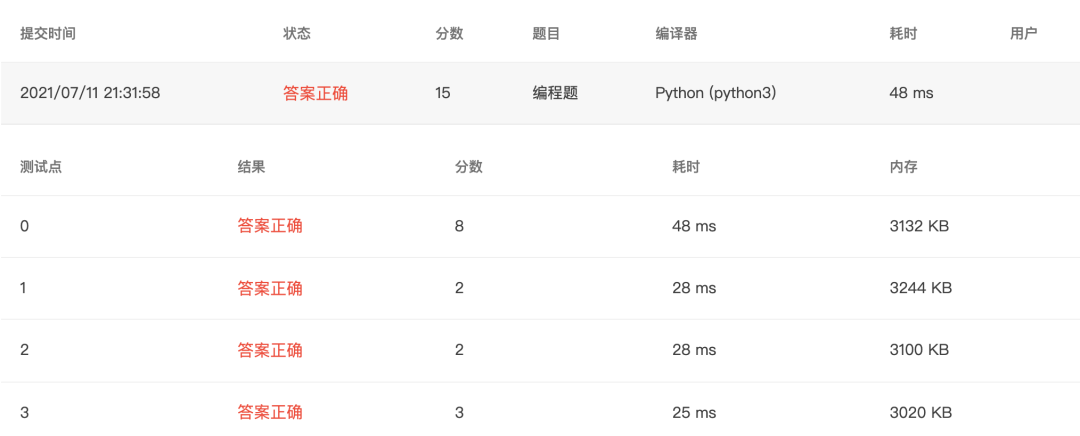
提交代码 - 2

n = int(input())
a = 2
b = 1
sum = 2
for i in range(n-1):
    a, b = a+b, a
    sum += a/b
print("{:.2f}".format(sum))

4-9 查询水果价格 (15 分)

题目

给定四种水果，分别是苹果（apple）、梨（pear）、桔子（orange）、葡萄（grape），单价分别对应为3.00元/公斤、2.50元/公斤、4.10元/公斤、10.20元/公斤。

首先在屏幕上显示以下菜单：

❝

[1] apple

[2] pear

[3] orange

[4] grape

[0] exit

用户可以输入编号1~4查询对应水果的单价。当连续查询次数超过5次时，程序应自动退出查询；不到5次而用户输入0即退出；输入其他编号，显示价格为0。

输入格式:

❝

输入在一行中给出用户连续输入的若干个编号。

输出格式:

❝

首先在屏幕上显示菜单。然后对应用户的每个输入，在一行中按格式“price = 价格”输出查询结果，其中价格保留两位小数。当用户连续查询次数超过5次、或主动输入0时，程序结束。

输入样例1:

❝

3 -1 0 2

输出样例1:

❝

[1] apple

[2] pear

[3] orange

[4] grape

[0] exit

price = 4.10

price = 0.00

输入样例2:

❝

1 2 3 3 4 4 5 6 7 8

输出样例2:

❝

[1] apple

[2] pear

[3] orange

[4] grape

[0] exit

price = 3.00

price = 2.50

price = 4.10

price = 4.10

price = 10.20

解答

goods = ["[1] apple", "[2] pear", "[3] orange", "[4] grape", "[0] exit"]
prices = ["3.00", "2.50", "4.10", "10.20"]
for i in goods:
    print(i)
lst = list(map(int, input().split()))
count = 0
for i in lst:
    count += 1
    if count > 5:
        exit()
    if 1 <= i <= 4:
        print("price = {}".format(prices[i-1]))
    elif i == 0:
        exit()
    else:
        print("price = 0.00")

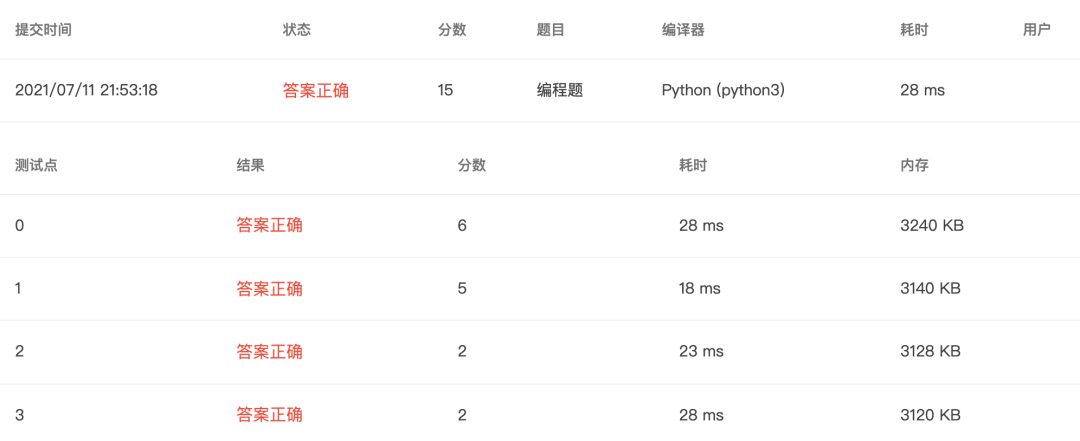
4-10 最大公约数和最小公倍数 (15 分)

题目

本题要求两个给定正整数的最大公约数和最小公倍数。

输入格式:

❝

输入在一行中给出两个正整数M和N（≤1000）。

输出格式:

❝

在一行中顺序输出M和N的最大公约数和最小公倍数，两数字间以1空格分隔。

输入样例:

❝

511 292

输出样例:

❝

73 2044

解答

def gcd(a, b):
    if a % b == 0:
        return b
    else:
        return gcd(b, a % b)


n, m = input().split()
n = int(n)
m = int(m)
print('{:d} {:d}'.format(gcd(n, m), n*m//gcd(n, m)))

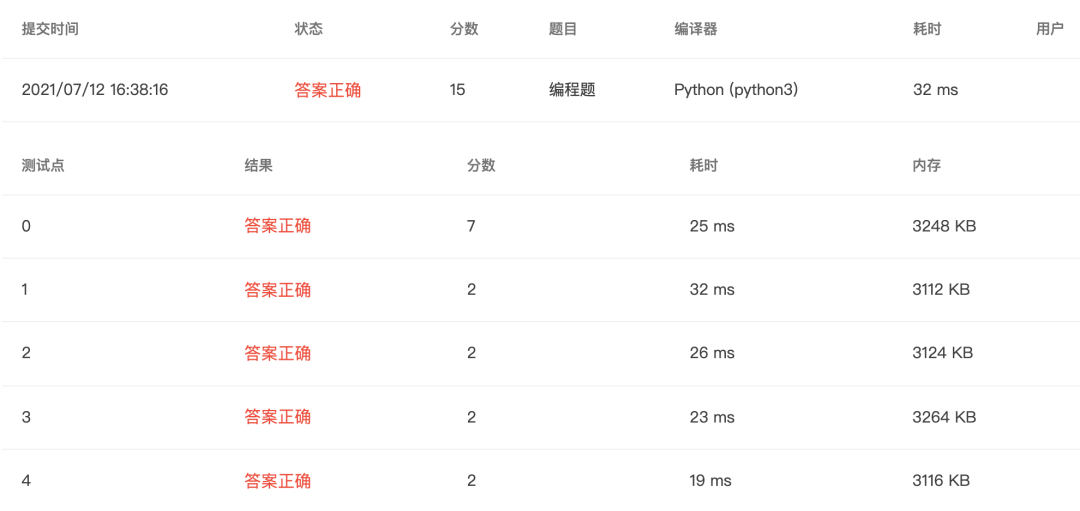
4-11 判断素数 (20 分)

题目

判断一个给定的正整数是否素数

输入格式:

❝

输入在第一行给出一个正整数N（≤ 10），随后N行，每行给出一个小于1000000 的需要判断的正整数

输出格式:

❝

对每个需要判断的正整数，如果它是素数，则在一行中输出Yes，否则输出No

输入样例: 在这里给出一组输入。例如：

❝

2 11 111

输出样例: 在这里给出相应的输出。例如：

❝

Yes No

解答

import math


def judge(num):
    if num == 1:
        return False
    for i in range(2, int(math.sqrt(num))+1):
        if num % i == 0:
            return False
    return True


n = int(input())
while n > 0:
    num = int(input())
    if judge(num):
        print("Yes")
    else:
        print("No")
    n -= 1

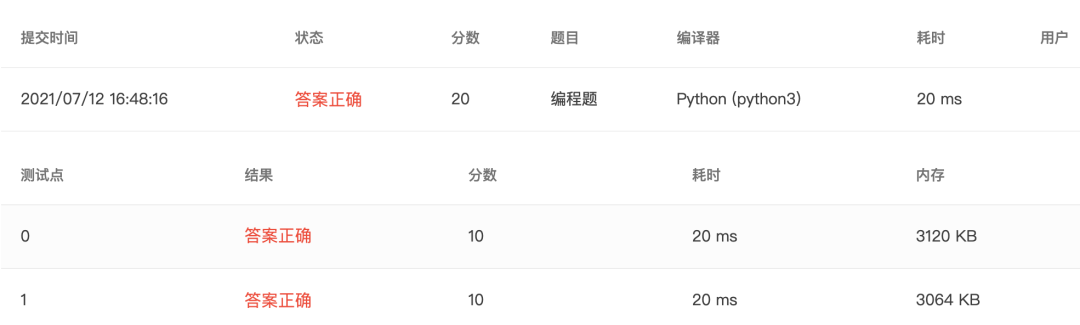
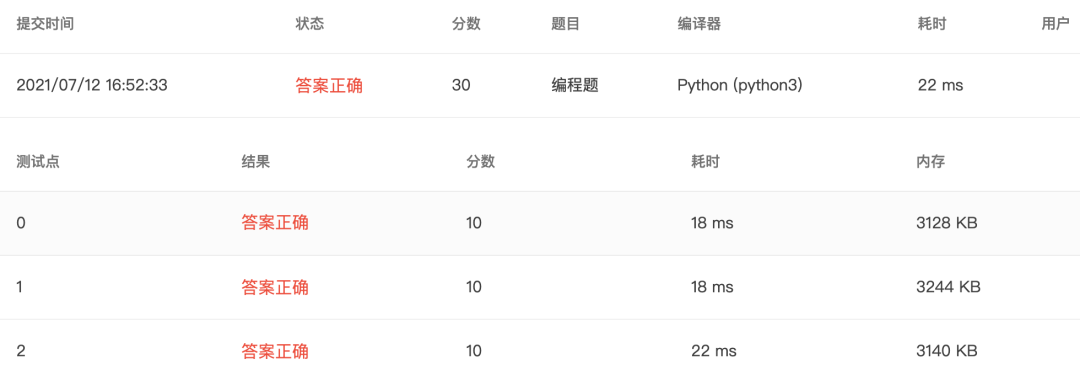
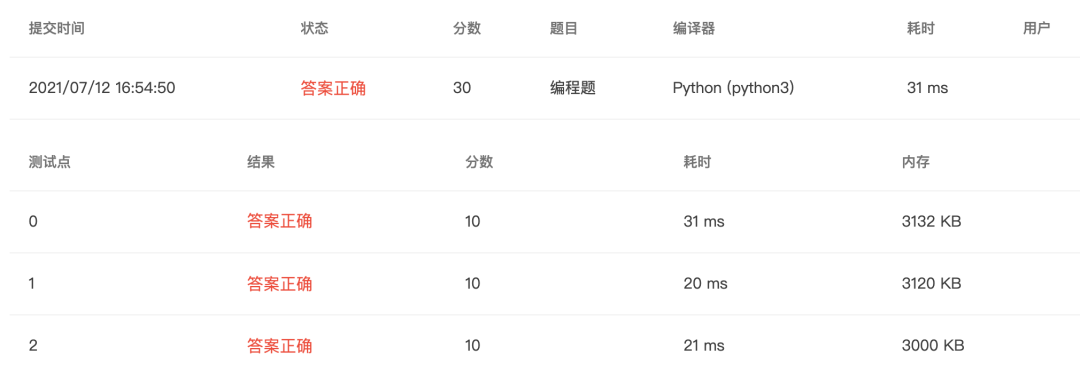
4-12 求满足条件的斐波那契数 (30 分)

题目

斐波那契数，亦称之为斐波那契数列，指的是这样一个数列：1、1、2、3、5、8、13、21、……，这个数列从第3项开始，每一项都等于前两项之和。求大于输入数的最小斐波那契数。

输入格式:

❝

在一行输人一个正整数n(n>=10)。

输出格式:

❝

在一行输出大于n的最小斐波那契数。

输入样例: 在这里给出一组输入。例如：

❝

10

输出样例: 在这里给出相应的输出。例如：

❝

13

解答

num = int(input())
a = 1
b = 1
c = a + b
while c < num:
    a, b = b, a+b
    c = a+b
print(c)

num = int(input())
a = 1
b = 1
while b < num:
    a, b = b, a+b
print(b)

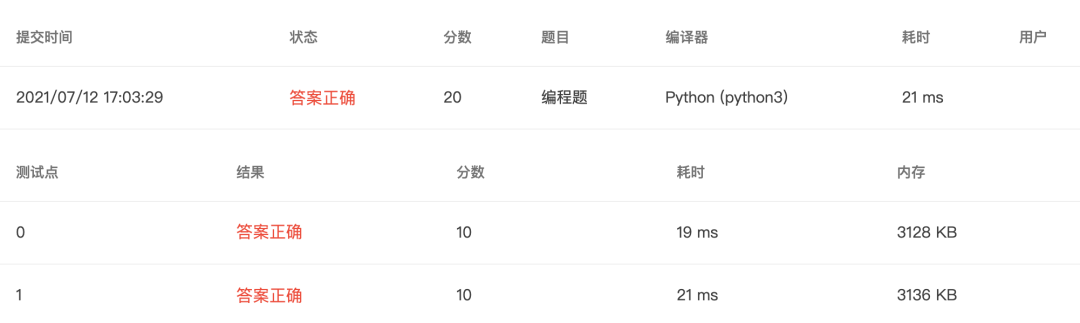
4-13 求误差小于输入值的e的近似值 (20 分)

题目

自然常数e可以用级数1+1/1!+1/2!+⋯+1/n!来近似计算。ei代表前i项求和。输入误差范围error,当 ei+1-ei<error,则表示e的近似值满足误差范围。

输入格式:

❝

在一行输入误差范围,误差小于等于0.01。

输出格式:

❝

在一行输出e的近似值（保留6位小数）。

输入样例1: 在这里给出一组输入。例如：

❝

0.01

输出样例1: 在这里给出相应的输出。例如：

❝

2.716667

输入样例2: 在这里给出一组输入。例如：

❝

0.000000001

输出样例2: 在这里给出相应的输出。例如：

❝

2.718282

解答

error = float(input())
sum = 1
count = 1
n = 1
while True:
    n = n*count
    count += 1
    sum += 1/n
    if 1/n < error:
        print("{:.6f}".format(sum))
        break

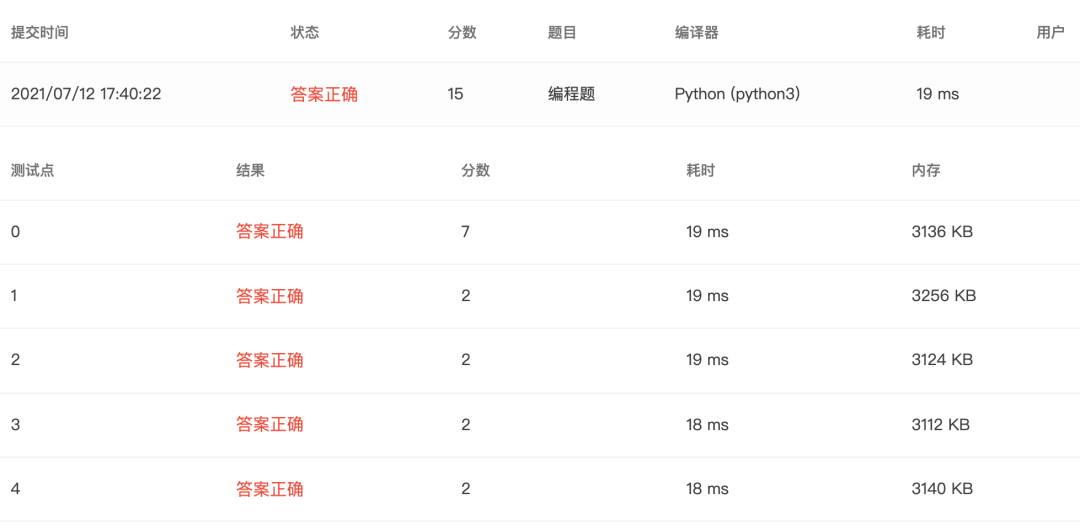
4-14 统计字符 (15 分)

题目

本题要求编写程序，输入10个字符，统计其中英文字母、空格或回车、数字字符和其他字符的个数。本题要求编写程序，输入10个字符，统计其中英文字母、空格或回车、数字字符和其他字符的个数。

输入格式:

❝

输入为10个字符。最后一个回车表示输入结束，不算在内。

输出格式: 在一行内按照

❝

letter = 英文字母个数, blank = 空格或回车个数, digit = 数字字符个数, other = 其他字符个数

的格式输出。

输入样例:

❝

aZ & 09 Az

输出样例:

❝

letter = 4, blank = 3, digit = 2, other = 1

解答

letter_nums = 0
blank_nums = 0
digit_nums = 0
other_nums = 0
count = 0
str = ""
while True:
    s = input()
    count += 1
    str += s
    if len(str)+count > 10:
        count -= 1
        break
blank_nums += count
for i in str:
    if i.isalpha():
        letter_nums += 1
    elif i.isspace():
        blank_nums += 1
    elif i.isdigit():
        digit_nums += 1
    else:
        other_nums += 1
print("letter = {}, blank = {}, digit = {}, other = {}".format(
    letter_nums, blank_nums, digit_nums, other_nums))

4-15 换硬币 (20 分)

题目

将一笔零钱换成5分、2分和1分的硬币，要求每种硬币至少有一枚，有几种不同的换法？

输入格式:

❝

输入在一行中给出待换的零钱数额x∈(8,100)。

输出格式:

❝

要求按5分、2分和1分硬币的数量依次从大到小的顺序，输出各种换法。每行输出一种换法，格式为：“fen5:5分硬币数量, fen2:2分硬币数量, fen1:1分硬币数量, total:硬币总数量”。最后一行输出“count = 换法个数”。

输入样例:

❝

13

输出样例:

❝

fen5:2, fen2:1, fen1:1, total:4

fen5:1, fen2:3, fen1:2, total:6

fen5:1, fen2:2, fen1:4, total:7

fen5:1, fen2:1, fen1:6, total:8

count = 4

解答

num = int(input())
count = 0
for i in range(num//5, 0, -1):
    for j in range(num//2, 0, -1):
        for k in range(num, 0, -1):
            if 5*i+2*j+k == num:
                print("fen5:{}, fen2:{}, fen1:{}, total:{}".format(i, j, k, i+j+k))
                count += 1
print("count = {}".format(count))

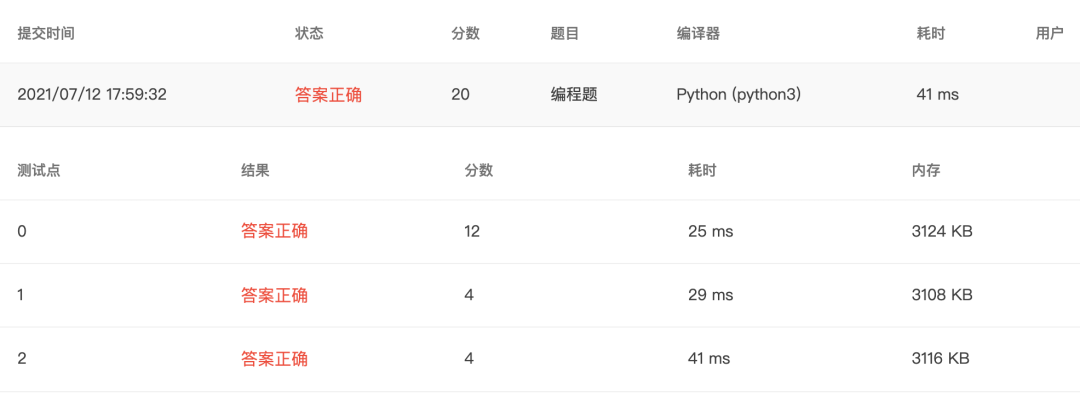
4-16 jmu-python-判断是否构成三角形 (10 分)

题目

输入三角形的三边，判断是否能构成三角形。若能构成输出yes，否则输出no。

输入格式:

❝

在一行中直接输入3个整数，3个整数之间各用一个空格间隔，没有其他任何附加字符。

输出格式:

❝

直接输出yes或no，没有其他任何附加字符。

输入样例1:

❝

3 4 5

输出样例1:

❝

yes

输入样例2:

❝

1 2 3

输出样例2:

❝

no

解答

a, b, c = map(int, input().split())
if a+b > c and a+c > b and b+c > a:
    print("yes")
else:
    print("no")

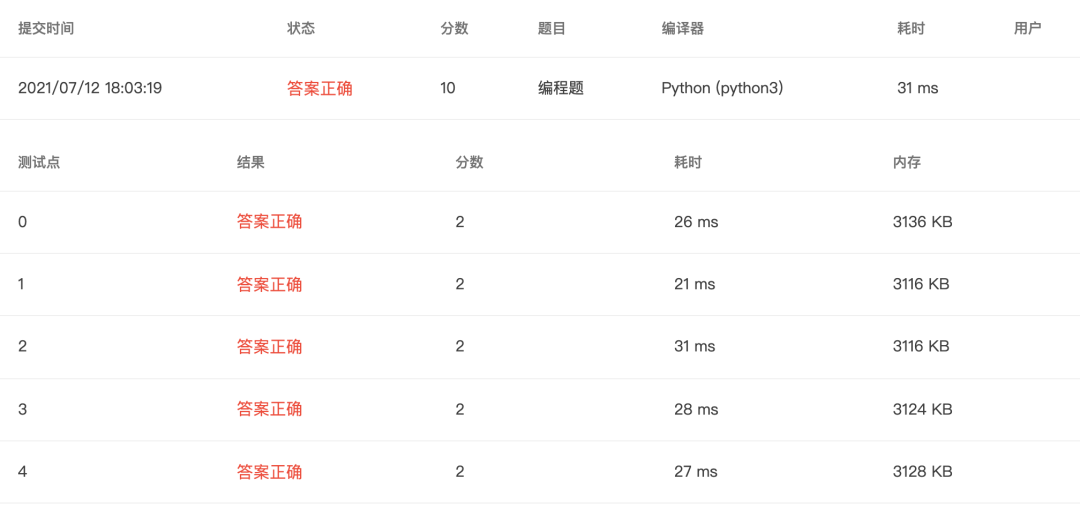
4-17 水仙花数（20 分） (20 分)

题目

水仙花数是指一个N位正整数（N≥3），它的每个位上的数字的N次幂之和等于它本身。例如：153=1×1×1+5×5×5+3×3×3。

本题要求编写程序,计算所有N位水仙花数。水仙花数是指一个N位正整数（N≥3），它的每个位上的数字的N次幂之和等于它本身。例如：153=1×1×1+5×5×5+3×3×3。本题要求编写程序,计算所有N位水仙花数。

输入格式:

❝

输入在一行中给出一个正整数N（3≤N≤5）

输出格式:

❝

按递增顺序输出所有N位水仙花数，每个数字占一行。

输入样例: 在这里给出一组输入。例如：

❝

3

输出样例: 在这里给出相应的输出。例如：

❝

153

370

371

407

解答

提交代码 - 1

def judge(num, n):
    sum = 0
    i = num
    while i > 0:
        sum += pow(i % 10, n)
        i //= 10
    if sum == num:
        return True
    else:
        return False


n = int(input())
for i in range(pow(10, n-1), pow(10, n)):
    if judge(i, n):
        print(i)

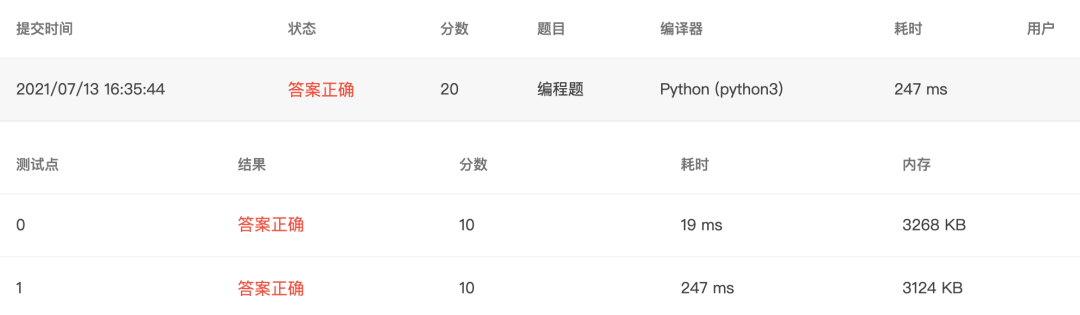
提交代码 - 2

n = int(input())
for num in range(10**(n-1), 10**n):
    lists = map(int, str(num))
    sum = 0
    for i in lists:
        sum += i**n
    if sum == num:
        print(num)

4-18 猴子选大王 (20 分)

题目

一群猴子要选新猴王。新猴王的选择方法是：让N只候选猴子围成一圈，从某位置起顺序编号为1~N号。从第1号开始报数，每轮从1报到3，凡报到3的猴子即退出圈子，接着又从紧邻的下一只猴子开始同样的报数。如此不断循环，最后剩下的一只猴子就选为猴王。请问是原来第几号猴子当选猴王？

输入格式：

❝

输入在一行中给一个正整数N（≤1000）。

输出格式：

❝

在一行中输出当选猴王的编号。

输入样例：

❝

11

输出样例：

❝

7

解答

n = int(input())
ans = 0
for i in range(2, n+1):
    ans = (ans+3) % i
print(ans+1)

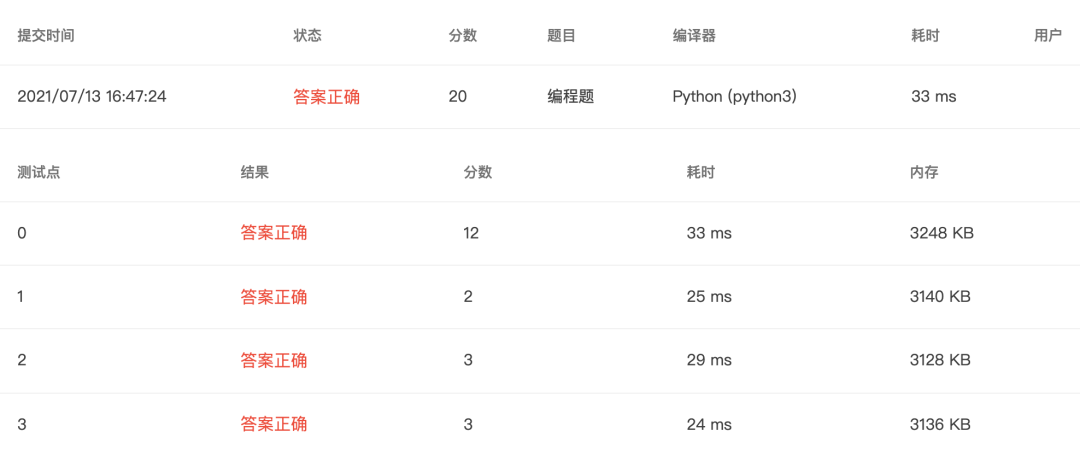
4-19 矩阵运算 (20 分)

题目

给定一个_n_×_n_的方阵，本题要求计算该矩阵除副对角线、最后一列和最后一行以外的所有元素之和。副对角线为从矩阵的右上角至左下角的连线。

输入格式:

❝

输入第一行给出正整数n（1<n≤10）；随后n行，每行给出n个整数，其间以空格分隔。

输出格式:

❝

在一行中给出该矩阵除副对角线、最后一列和最后一行以外的所有元素之和。

输入样例:

❝

4 2 3 4 1 5 6 1 1 7 1 8 1 1 1 1 1

输出样例:

❝

35

解答

n = int(input())
index = n-1
ans = 0
while n > 1:
    lst = list(map(int, input().split()))
    for i, num in enumerate(lst):
        if i != len(lst)-1 and i != index:
            ans += num
    index -= 1
    n -= 1
print(ans)

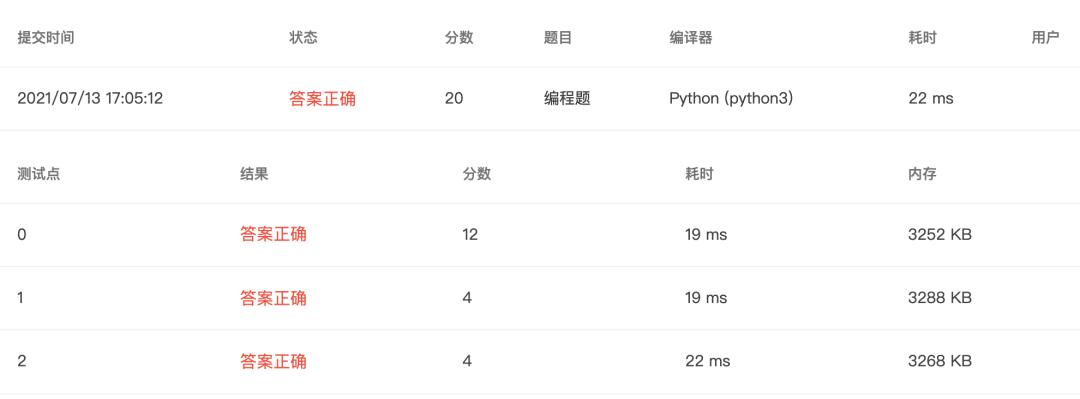
4-20 求矩阵各行元素之和 (15 分)

题目

本题要求编写程序，求一个给定的_m_×_n_矩阵各行元素之和。

输入格式：

❝

输入第一行给出两个正整数m和n（1≤m,n≤6）。随后m行，每行给出n个整数，其间以空格分隔。

输出格式：

❝

每行输出对应矩阵行元素之和。

输入样例：

❝

3 2 6 3 1 -8 3 12

输出样例：

❝

9 -7 15

解答

m, n = map(int, input().split())
while m:
    lst = list(map(int, input().split()))
    sum = 0
    for i in lst:
        sum += i
    m -= 1
    print(sum)

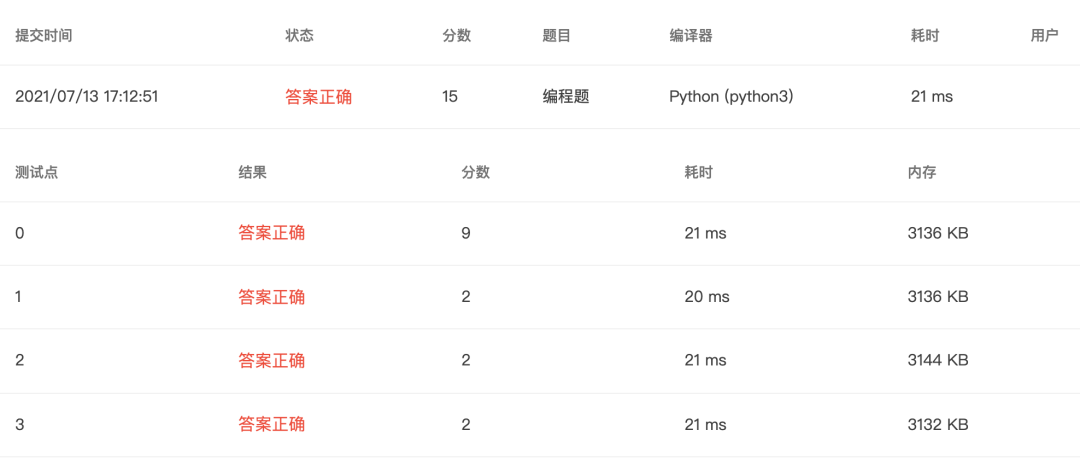
4-21 判断上三角矩阵 (15 分)

题目

上三角矩阵指主对角线以下的元素都为0的矩阵；主对角线为从矩阵的左上角至右下角的连线。本题要求编写程序，判断一个给定的方阵是否上三角矩阵。

输入格式：

❝

输入第一行给出一个正整数T，为待测矩阵的个数。接下来给出T个矩阵的信息：每个矩阵信息的第一行给出一个不超过10的正整数n。随后n行，每行给出n个整数，其间以空格分隔。

输出格式：

❝

每个矩阵的判断结果占一行。如果输入的矩阵是上三角矩阵，输出“YES”，否则输出“NO”。

输入样例：

❝

3

3

1 2 3

0 4 5

0 0 6

2

1 0

-8 2

3

1 2 3

1 4 5

0 -1 6

输出样例：

❝

YES NO NO

解答

def judge(a):
    for i in range(len(a)):
        for j in range(len(a)):
            if i > j and a[i][j] != 0:
                return False
    return True


t = int(input())
while t:
    n = int(input())
    a = []
    while n:
        s = input()
        a.append([int(i) for i in s.split()])
        n -= 1
    if judge(a):
        print("YES")
    else:
        print("NO")
    t -= 1

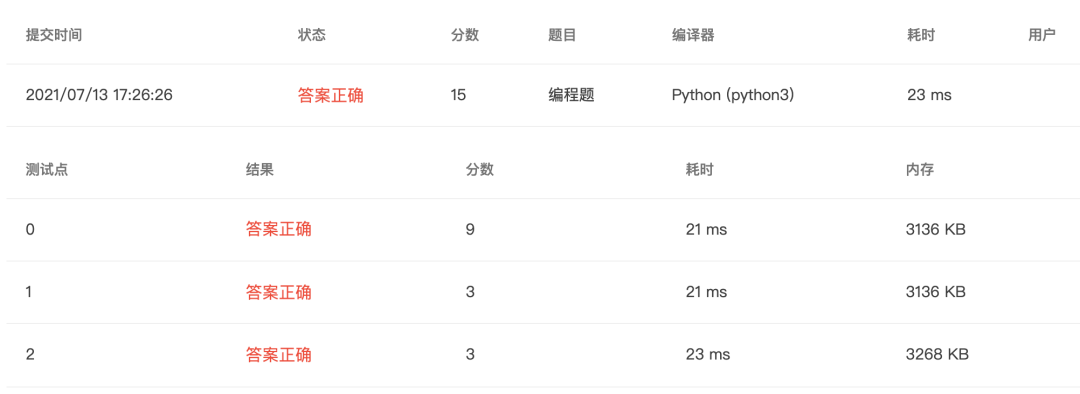
4-22 找鞍点 (20 分)

题目

一个矩阵元素的“鞍点”是指该位置上的元素值在该行上最大、在该列上最小。

本题要求编写程序，求一个给定的n阶方阵的鞍点。

输入格式：

❝

输入第一行给出一个正整数n（1≤n≤6）。随后n行，每行给出n个整数，其间以空格分隔。

输出格式：

❝

输出在一行中按照“行下标 列下标”（下标从0开始）的格式输出鞍点的位置。如果鞍点不存在，则输出“NONE”。题目保证给出的矩阵至多存在一个鞍点。

输入样例1：

❝

4

1 7 4 1

4 8 3 6

1 6 1 2

0 7 8 9

输出样例1：

❝

2 1

输入样例2：

❝

2 1 7 4 1

输出样例2：

❝

NONE

解答

n = int(input())
a = []
for i in range(n):
    a.append(list(map(int, input().split())))
for i in range(n):
    max_num_row = max(a[i][k] for k in range(n))
    for j in range(n):
        max_num_col = min(a[k][j] for k in range(n))
        if max_num_row == max_num_col:
            print("{} {}".format(i, j))
            exit()
print("NONE")

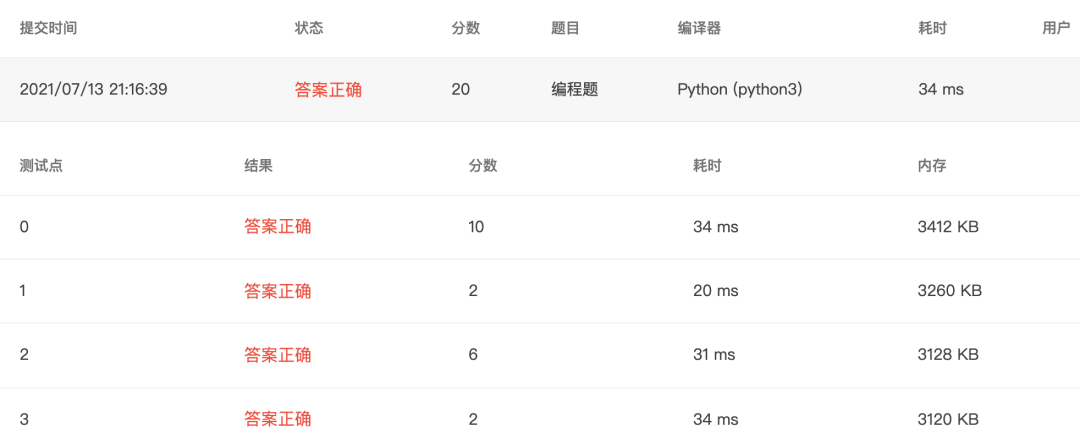
4-23 求矩阵的局部极大值 (15 分)

题目

给定_M_行_N_列的整数矩阵_A_，如果_A_的非边界元素_A_[i][j]大于相邻的上下左右4个元素，那么就称元素_A_[i][j]是矩阵的局部极大值。本题要求给定矩阵的全部局部极大值及其所在的位置。

输入格式：

❝

输入在第一行中给出矩阵A的行数M和列数N（3≤M,N≤20）；最后M行，每行给出A在该行的N个元素的值。数字间以空格分隔。

输出格式：

❝

每行按照“元素值 行号 列号”的格式输出一个局部极大值，其中行、列编号从1开始。要求按照行号递增输出；若同行有超过1个局部极大值，则该行按列号递增输出。若没有局部极大值，则输出“None 总行数 总列数”。

输入样例1：

❝

4 5

1 1 1 1 1

1 3 9 3 1

1 5 3 5 1

1 1 1 1 1

输出样例1：

❝

9 2 3

5 3 2

5 3 4

输入样例2：

❝

3 5

1 1 1 1 1

9 3 9 9

1 1 5 3 5 1

输出样例2：

❝

None 3 5

解答

m, n = map(int, input().split())
a = []
count = 0
for i in range(m):
    a.append(list(map(int, input().split())))
for i in range(1, m-1):
    for j in range(1, n-1):
        if a[i][j] > a[i-1][j] and a[i][j] > a[i][j+1] and a[i][j] > a[i+1][j] and a[i][j] > a[i][j-1]:
            print("{} {} {}".format(a[i][j], i+1, j+1))
            count += 1
if count == 0:
    print("None {} {}".format(m, n))

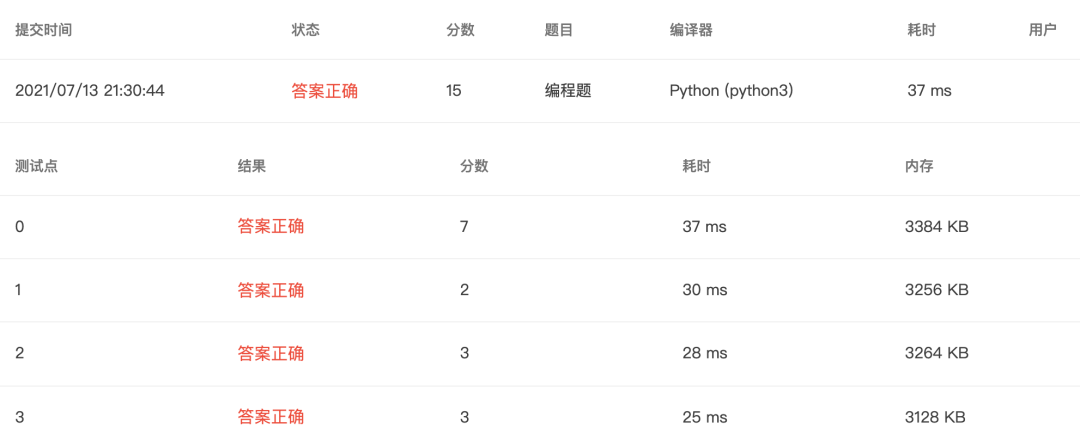
4-24 打印九九口诀表 (15 分)

题目

下面是一个完整的下三角九九口诀表：

❝

1*1=1

12=2   22=4

13=3   23=6   3*3=9

14=4   24=8   34=12  44=16

15=5   25=10  35=15  45=20  5*5=25

16=6   26=12  36=18  46=24  56=30  66=36

17=7   27=14  37=21  47=28  57=35  67=42  77=49 >
18=8   28=16  38=24  48=32  58=40  68=48  78=56  8*8=64

19=9   29=18  39=27  49=36  59=45  69=54  79=63  89=72  9*9=81

本题要求对任意给定的一位正整数N，输出从11到NN的部分口诀表。

输入格式：

❝

输入在一行中给出一个正整数N（1≤N≤9）。

输出格式：

❝

输出下三角N*N部分口诀表，其中等号右边数字占4位、左对齐。

输入样例：

❝

4

输出样例：

❝

1*1=1

12=2   22=4

13=3   23=6   3*3=9

14=4   24=8   34=12  44=16

解答

n = int(input())
for i in range(1, n+1):
    for j in range(1, n+1):
        if i >= j:
            print("{}*{}={:<4d}".format(j, i, i*j), end="")
    print()

4-25 输出三角形字符阵列 (15 分)

题目

本题要求编写程序，输出n行由大写字母A开始构成的三角形字符阵列。

输入格式：

❝

输入在一行中给出一个正整数n（1≤n<7）。

输出格式：

❝

输出n行由大写字母A开始构成的三角形字符阵列。格式见输出样例，其中每个字母后面都有一个空格。

输入样例：

❝

4

输出样例：

❝

A B C D
E F G
H I
J

解答

n = int(input())
count = 0
while n:
    for i in range(1, n+1):
        print("{} ".format(chr(ord('A')+count)), end="")
        count += 1
    print()
    n -= 1

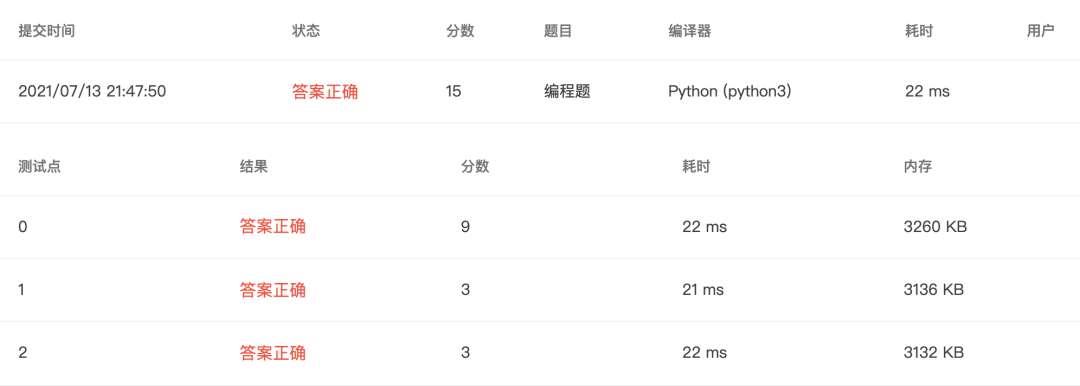
4-26 求1!+3!+5!+……+n! (10 分)

题目

求1!+3!+5!+……+n!的和，要求用循环嵌套设计，n<12。输入格式:

❝

输入在一行中给出一个不超过12的正整数n。

输出格式:

❝

在一行中按照格式“n=n值,s=阶乘和”的顺序输出，其中阶乘和是正整数。

输入样例:

❝

5

输出样例:

❝

n=5,s=127

解答

n = int(input())
t = 1
sum = 1
for i in range(1, n+1, 2):
    if i != 1:
        for j in range(i-1, i+1):
            t *= j
        sum += t
print("n={},s={}".format(n, sum))

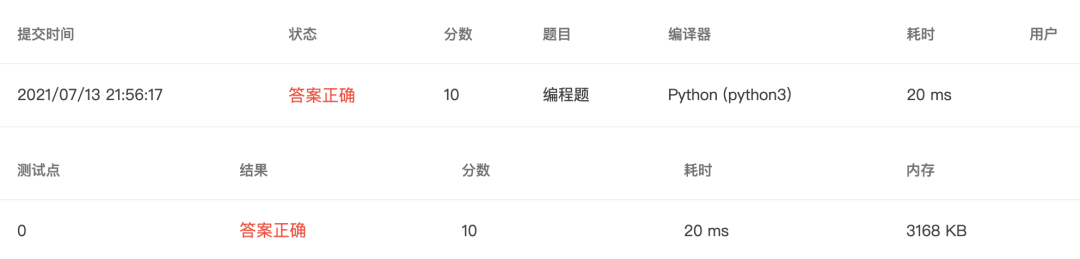
4-27 二维数组中每行最大值和每行和 (10 分)

题目

求一个3*3二维数组中每行的最大值和每行的和。输入格式:

❝

在一行中输入9个小于100的整数，其间各以一个空格间隔

输出格式:

❝

输出3行3列的二维数组，并在每行后面分别输出每行最大值和每行元素的和，每个数据输出占4列。

输入样例:

❝

3 6 5 9 8 2 1 4 5

输出样例:

❝

3   6   5   6  14
9   8   2   9  19
1   4   5   5  10

解答

lst = list(map(int, input().split()))
for i in range(3):
    max_num = lst[i*3]
    sum = 0
    for j in range(3):
        max_num = max(max_num, lst[i*3+j])
        sum += lst[i*3+j]
        print("{:4d}".format(lst[i*3+j]), end="")
    print("{:4d}{:4d}".format(max_num, sum))

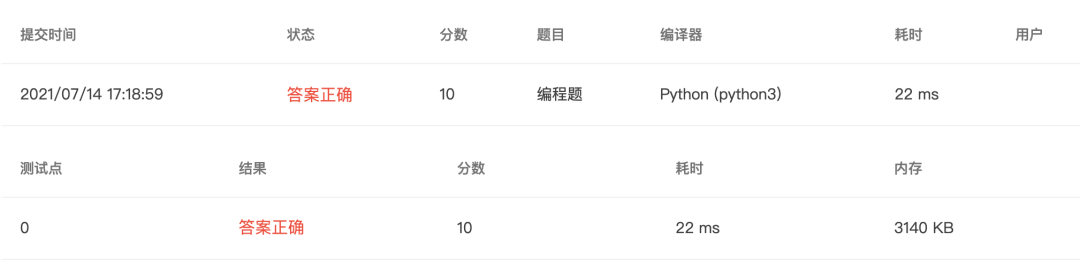
4-28 矩阵转置 (10 分)

题目

将一个3×3矩阵转置（即行和列互换）。

输入格式:

❝

在一行中输入9个小于100的整数，其间各以一个空格间隔。

输出格式:

❝

输出3行3列的二维数组，每个数据输出占4列。

输入样例:

❝

1 2 3 4 5 6 7 8 9

输出样例:

❝

1   4   7
2   5   8
3   6   9

解答

lst = list(map(int, input().split()))
for i in range(3):
    for j in range(3):
        print("{:4d}".format(lst[i+j*3]), end="")
    print()

4-29 找出不是两个数组共有的元素 (20 分)

题目

给定两个整型数组，本题要求找出不是两者共有的元素。

输入格式:

❝

输入分别在两行中给出两个整型数组，每行先给出正整数N（≤20），随后是N个整数，其间以空格分隔。

输出格式:

❝

在一行中按照数字给出的顺序输出不是两数组共有的元素，数字间以空格分隔，但行末不得有多余的空格。题目保证至少存在一个这样的数字。同一数字不重复输出。

输入样例:

❝

10 3 -5 2 8 0 3 5 -15 9 100 11 6 4 8 2 6 -5 9 0 100 8 1

输出样例:

❝

3 5 -15 6 4 1

解答

注意：返回答案的顺序也是有要求的 暴力解法

lst1 = list(map(int, input().split()))
lst2 = list(map(int, input().split()))
lst1 = lst1[1:]
lst2 = lst2[1:]
ans = []
for i in lst1:
    if i not in lst2 and i not in ans:
        ans.append(i)
for i in lst2:
    if i not in lst1 and i not in ans:
        ans.append(i)
for i, num in enumerate(ans):
    if i != len(ans)-1:
        print("{} ".format(num), end="")
    else:
        print("{}".format(num))

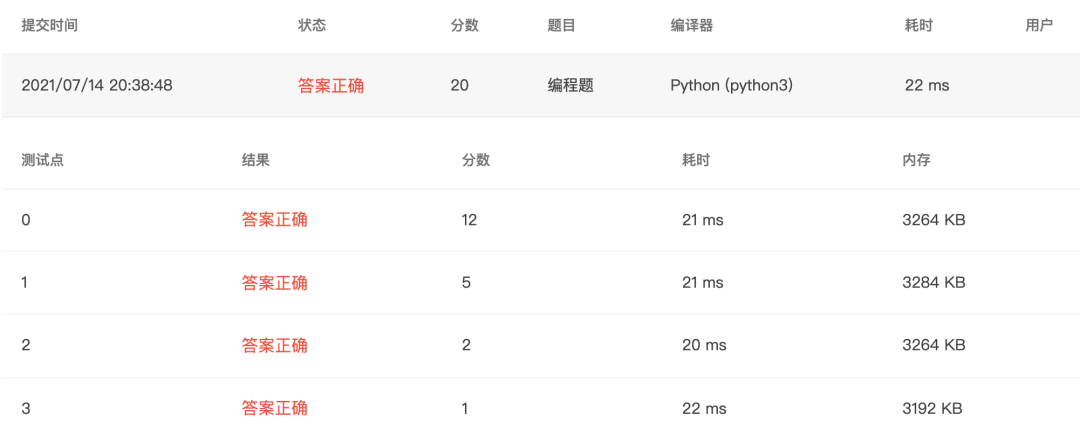
4-30 找完数 (20 分)

题目

所谓完数就是该数恰好等于除自身外的因子之和。例如：6=1+2+3，其中1、2、3为6的因子。本题要求编写程序，找出任意两正整数m和n之间的所有完数。

输入格式：

❝

输入在一行中给出2个正整数m和n（1<m≤n≤10000），中间以空格分隔。

输出格式：

❝

逐行输出给定范围内每个完数的因子累加形式的分解式，每个完数占一行，格式为“完数 = 因子1 + 因子2 + ... + 因子k”，其中完数和因子均按递增顺序给出。若区间内没有完数，则输出“None”。

输入样例：

❝

2 30

输出样例：

❝

6 = 1 + 2 + 3 28 = 1 + 2 + 4 + 7 + 14

解答

暴力

import math
m, n = map(int, input().split())
count = 0
for i in range(m, n+1):
    ans = []
    for j in range(1, i):
        if i % j == 0:
            ans.append(j)
    if sum(ans) == i:
        count += 1
        print("{} = ".format(i), end="")
        print(' + '.join('%s' % id for id in ans))
if count == 0:
    print("None")

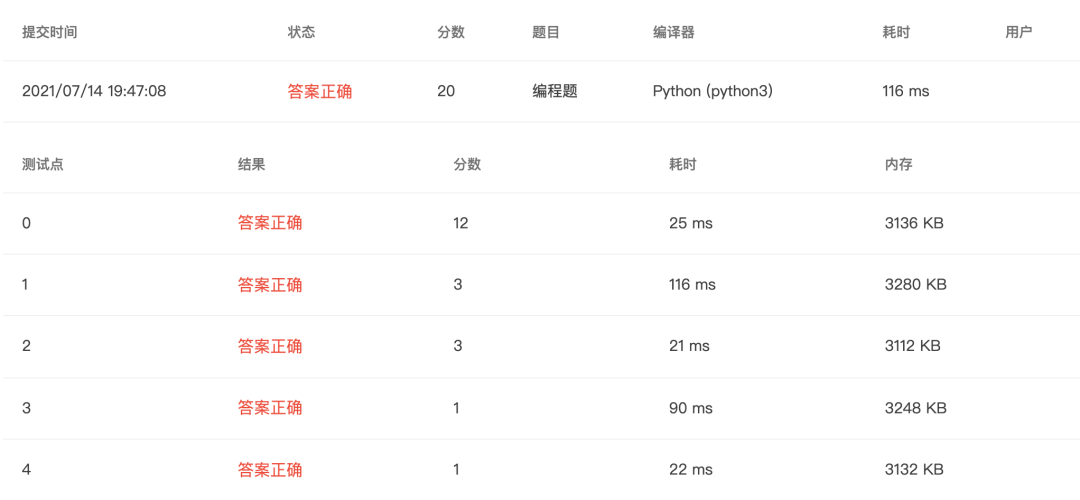
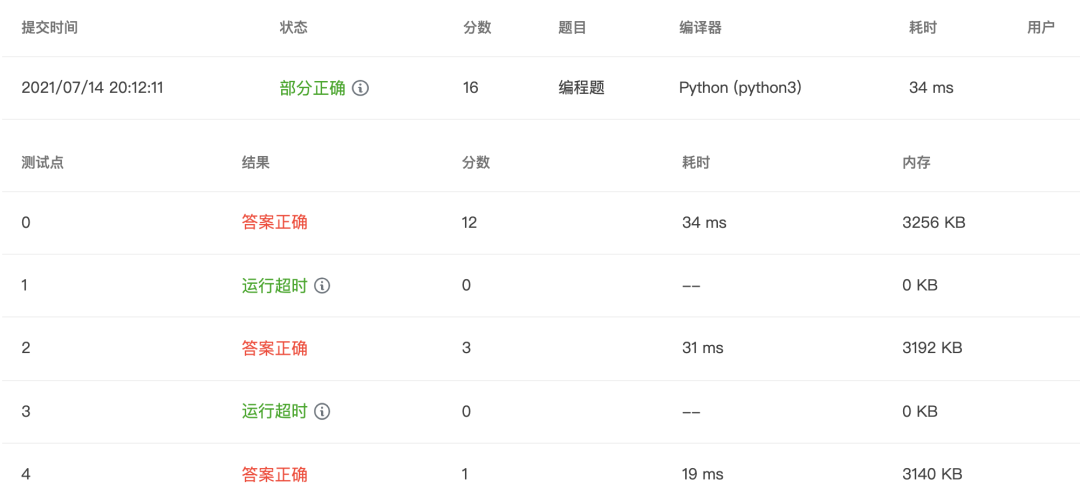优化后

import math
m, n = map(int, input().split())
count = 0
for i in range(m, n+1):
    ans = []
    ans.append(1)
    for j in range(2, int(math.sqrt(i)+1)):
        if i % j == 0:
            ans.append(j)
            if j*j != i:
                ans.append(i//j)
    if sum(ans) == i:
        count += 1
        ans.sort()
        print("{} = ".format(i), end="")
        print(' + '.join('%s' % id for id in ans))
if count == 0:
    print("None")

结语

文章仅作为学习笔记，记录从0到1的一个过程

希望对您有所帮助，如有错误欢迎小伙伴指正～

我是 海轰ଘ(੭ˊᵕˋ)੭

如果您觉得写得可以的话，请点个赞吧

谢谢支持❤️