面试高频考题——手撸一个 LRU 算法!
今天给大家讲一道面试中经常容易遇到的一道题:“手写一个 LRU 算法”。
LRU 就是 Least Recently Used 的缩写,翻译过来就是“最近最少使用”。 也就是说 LRU 算法会将最近最少用的缓存移除,让给最新使用的缓存。这是非常常见的一个缓存淘汰策略。
利用好 LRU 算法,我们能够提高对热点数据的缓存效率,进而提升缓存服务的内存使用率。
那么如何实现呢?
其实,通过缓存的 key 获取其对应的缓存,我们应该能想到用哈希表来实现,毕竟这是一个键值对结构,可以在 O(1) 时间内获取 key 对应的缓存值。
但是,哈希表本身是无序的,因此,我们还需要一个类似于队列的数据结构来记录访问的先后顺序,将最近访问的数据放在头部(如下图),移除最后一项数据(最旧),我们可以用双向链表来实现数据的增删以及顺序的调整。
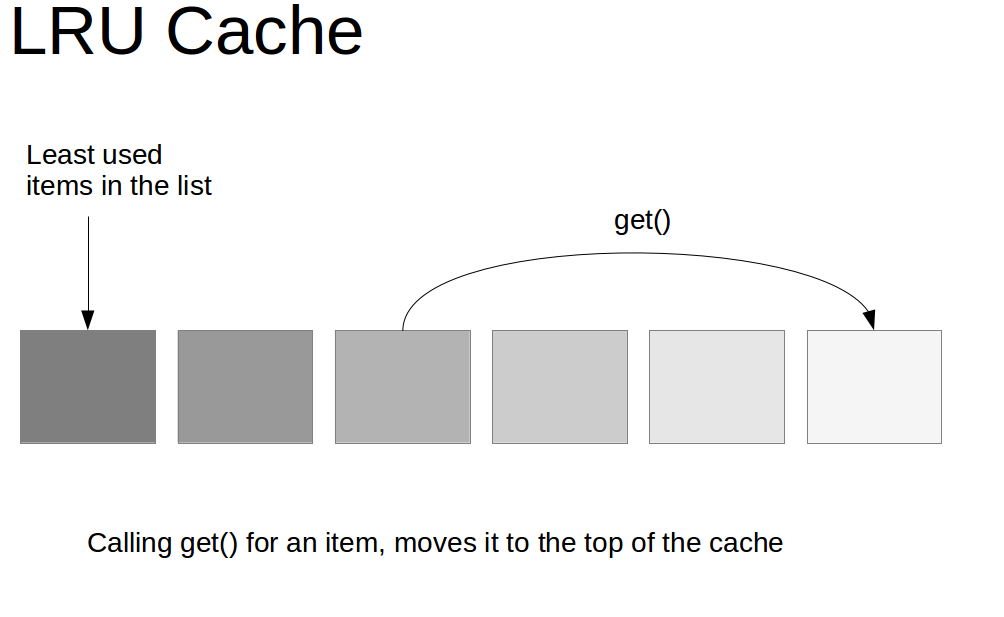
因此,我们结合“哈希表 + 双向链表”来实现 LRU 算法。其中:
•双向链表按照被使用的顺序存储 kv 键值对,靠近头部的 kv 键值对是最近使用的,而靠近尾部的键值对是最久未使用的。•哈希表通过缓存的 key 映射到双向链表中的位置。我们可以在 O(1) 时间内定位到缓存的 key 所对应的 value 在链表中的位置。
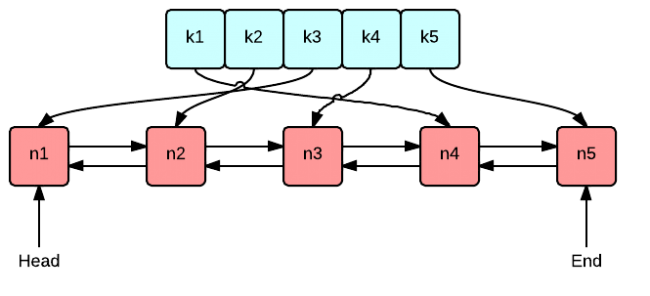
对于 get 操作,判断 key 是否存在哈希表中:
•若不存在,返回 -1。•若存在,则 key 对应的节点 node 是最近使用的节点。将该节点移动到双向链表的头部,最后返回该节点的值即可。
对于 put 操作,同样先判断 key 是否存在哈希表中:
•若不存在,则创建一个新的 node 节点,放入哈希表中。然后在双向链表的头部添加该节点。接着判断双向链表节点数是否超过 capacity。若超过,则删除双向链表的尾部节点,并且删除哈希表中对应的项。•若存在,则更新 node 节点的值,然后该节点移动到双向链表的头部。
双向链表节点(哈希表的 value)的结构如下:
class Node {int key;int value;Node prev;Node next;Node() {}Node(int key, int value) {this.key = key;this.value = value;}}
你可能会问,哈希表的 value 为何还要存放 key?
这是因为,双向链表有一个删除尾节点的操作。我们定位到双向链表的尾节点,在链表中删除之后,还要找到该尾节点在哈希表中的位置,因此需要根据 value 中存放的 key,定位到哈希表的数据项,然后将其删除。
以下是 Java 版本代码的完整实现。
class LRUCache {class Node {int key;int value;Node prev;Node next;Node() {}Node(int key, int value) {this.key = key;this.value = value;}}private int size;private int capacity;private Map<Integer, Node> cache;/* 虚拟头节点 */private Node head;/* 虚拟尾节点 */private Node tail;public LRUCache(int capacity) {this.size = 0;this.capacity = capacity;cache = new HashMap<>();head = new Node();tail = new Node();head.next = tail;tail.prev = head;}public int get(int key) {Node node = cache.get(key);if (node == null) {return -1;}// 将最近这次访问的数据移到头部moveToHead(node);return node.value;}public void put(int key, int value) {Node node = cache.get(key);if (node == null) {Node newNode = new Node(key, value);cache.put(key, newNode);// 将最近新增的数据放到头部addToHead(newNode);++size;// 若数据量超过设定的最大容量,移除尾部(最不常访问)的节点数据if (size > capacity) {Node tail = removeTail();// 缓存淘汰,移除尾部节点数据cache.remove(tail.key);--size;}} else {node.value = value;moveToHead(node);}}private void moveToHead(Node node) {removeNode(node);addToHead(node);}private void removeNode(Node node) {node.prev.next = node.next;node.next.prev = node.prev;}private void addToHead(Node node) {node.next = head.next;head.next = node;node.next.prev = node;node.prev = head;}private Node removeTail() {Node node = tail.prev;removeNode(node);return node;}}
长按识别下图二维码,关注公众号「Doocs 开源社区」,第一时间跟你们分享好玩、实用的技术文章与业内最新资讯。
