基于差分的求和方法 与 阿贝尔变换

这里介绍基于差分的有限项求和方法，并引出分部求和公式——「阿贝尔变换」

abstract.png 基于差分的求和方法

函数的前向差分通常简称为函数的差分。定义如下：

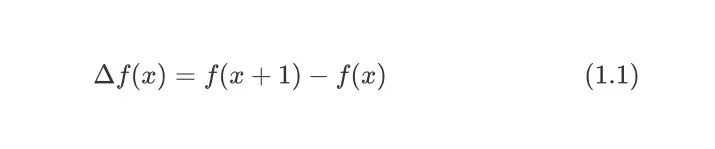figure 1.jpeg

其中，𝛥为差分算子。这里令g(x)为f(x)差分后的函数

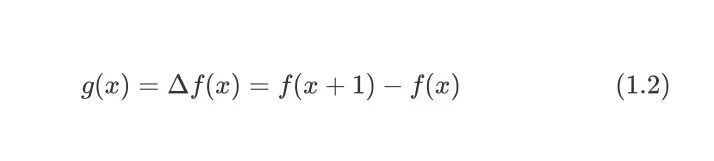figure 2.jpeg

则对g(x)的求和过程可转换为对原函数f(x)的计算，即：

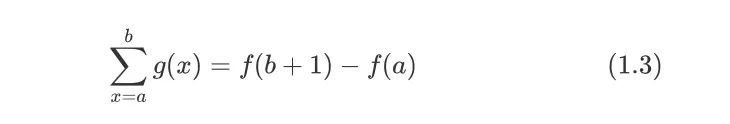figure 3.jpeg

事实上，证明(1.3)式也很简单，如下

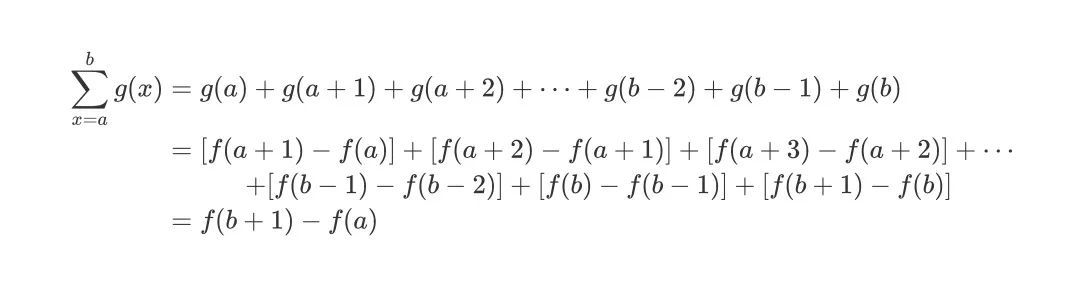figure 4.jpeg 升阶乘、降阶乘

这里，我们在指数m处使用上划线表示升阶乘。表示有m个因子一直向上乘

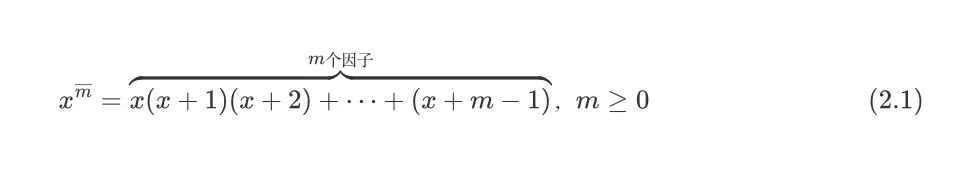figure 5.jpeg

同理，可以在指数m处使用下划线表示降阶乘。表示有m个因子一直向下乘

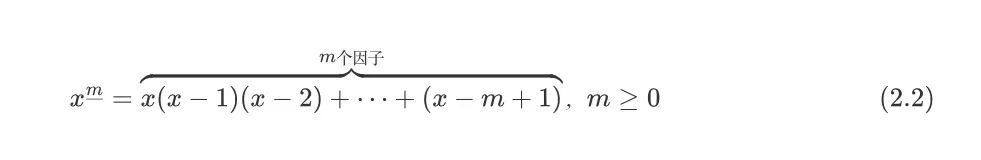figure 6.jpeg

特别地：

figure 7.jpeg 常用差分-逆差分对

从上不难看出，在对g(x)求和时，可将g(x)视为f(x)的差分。此时我们只需找出g(x)的逆差分函数f(x)即可。这里给出常用的差分-逆差分对

figure 8.jpeg

这里对移位算子E进行说明

figure 9.jpeg

对于上表的常用差分-逆差分对，我们选择最后一个进行证明，如下所示

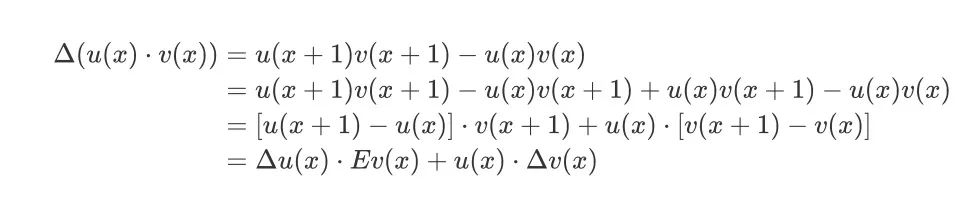figure 10.jpeg

之所以要对最后一个进行特别强调，是因为它暗含了一个与分部积分类似的分部求和方法。即所谓的「阿贝尔变换」

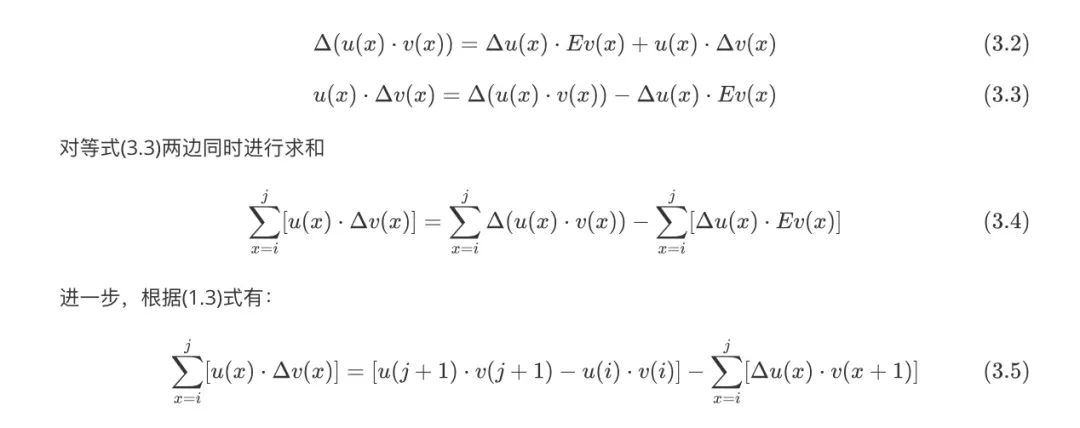figure 11.jpeg 参考文献

1. 具体数学 · 第2版 Ronald L.Graham、Oren Patashnik、Donald E.Knuth著