图网络(GNN)前传 : 图与矩阵的兄弟情结
为什么说 Graph 和 Matrix 是兄弟呢?因为它们有同一个爹!
矩阵的历史我们见识过了,知道 Matrix 一词是由英国(废话,这是英文单词,难道由法国人或者德国人首创吗)数学家西尔维斯特(Sylvester)在 1850 年首次在论文中引入的。
那么,Graph 这个英文单词呢?
1图论简史
上图中两个小岛与河的两岸共有七座桥连通,在每座桥都只能走一遍的前提下,如何才能把这七座桥都走遍呢?
这个就是所谓的柯尼斯堡七桥问题,也是现在小学生玩的一笔画问题的历史来源。
下面简要介绍一下图论的历史。
1735 年,有几名大学生写信给当时正在俄国彼得斯堡科学院任职的欧拉(Euler),请他帮忙解决柯尼斯堡七桥问题。欧拉于 1736 年发表的关于柯尼斯堡七桥的论文被认为是图论历史上的第一篇论文。 该论文发表一个多世纪之后,英国数学家及矩阵代数理论开拓者凯莱(Cayley)研究了一类特定的图,即树。这项研究对理论化学有许多启示,后来图论标准术语的一部分就是来自数学和化学两个领域中的思想融合。 而 Graph 一词由西尔维斯特在 1878 年发表于《自然》的一篇论文《化学和代数》中引入的。他在代数运算和分子图之间作了类比,还给出了图的几何乘法的规则,即用图的乘积构造图。
好了,原来这两个词是由同一个数学家引入的。看来它俩天生是一对好兄弟?
实际上,图和矩阵确实能相互表示,是一对可以互诉衷肠的好兄弟。但既然矩阵这词先出生,本篇就先来看看用矩阵表示图的常见方式。先简单概括下,用矩阵表示图有许多优点,
可以使用代数方法来研究图论;
对矩阵作分析可以得到图的性质; 以矩阵的形式存储和处理图的有关信息。
2图论基本概念
.图(Graph)
定义: 设
注:
本文只考虑无向图,即边是没有方向的。 在图中,若边 ,则称节点 与节点 相邻接;并说节点 与边 相关联,节点 与边 相关联;若边 和边 有一个共同的端点,则称边 和边 相邻接。 在图中,两端点相同的边称为环;两个节点间如果有多条边,则称为平行边。有平行边的图称为多重图(Multigraph),带环的图称为带环图,没有环也没有平行边的图,称为简单图。
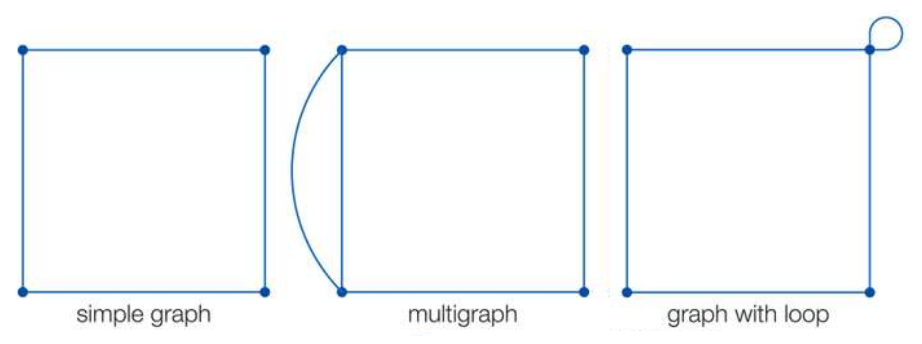
下图所示的三个图分别是简单图、多重图以及带环图。
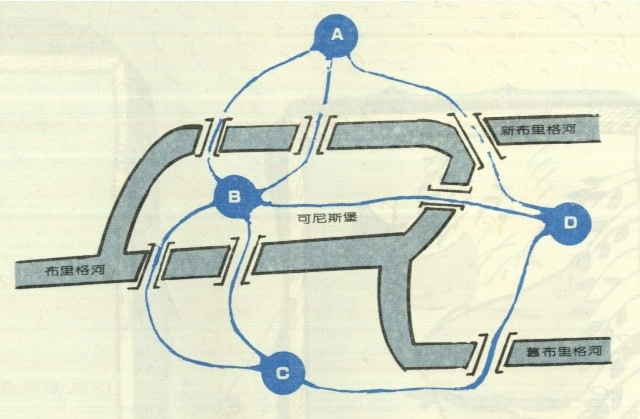
最终转化为如下所示的具有 4 个节点和 7 条边的图。
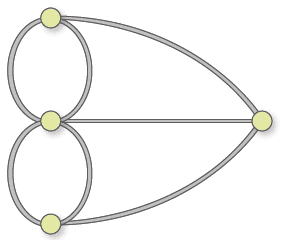
通,这个通可以是物理上走得通,也可以是抽象意义上的通,例如心灵上能够沟通。
那么请问该如何用一个图来表示这几口猿之间的沟通关系呢?假设至少懂同一种语言算作可以沟通。
.通路(Path)
在图论中,图中的通路是指一个由有限或无限条相邻接的边组成的边序列。通路中边的条数称为通路的长度。
请指出下图中桔红色粗线条指示的通路及其长度。
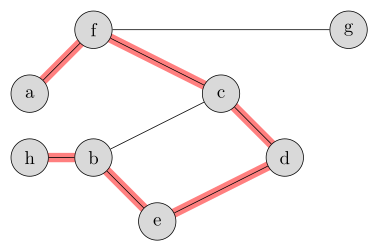
.距离(Distance)
图中节点
3图的矩阵表示
.邻接矩阵(Adjacency matrix)
需要注意的是,邻接矩阵并不唯一,换句话说,它依赖于
例 1 计算下图的邻接矩阵。
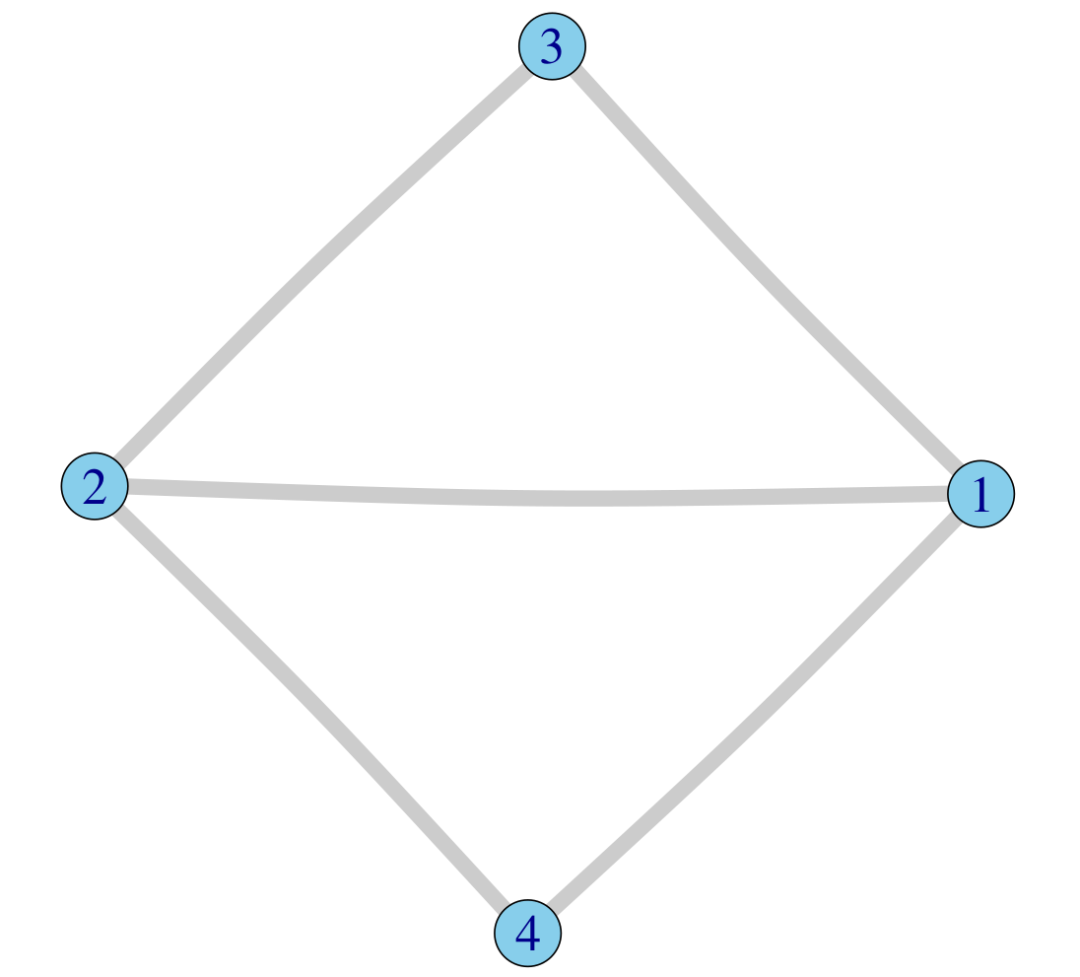
根据节点编号,我们计算邻接矩阵的各个元素如下,
[,1] [,2] [,3] [,4]
[1,] 0 1 1 1
[2,] 1 0 1 1
[3,] 1 1 0 0
[4,] 1 1 0 0
因此,邻接矩阵为,
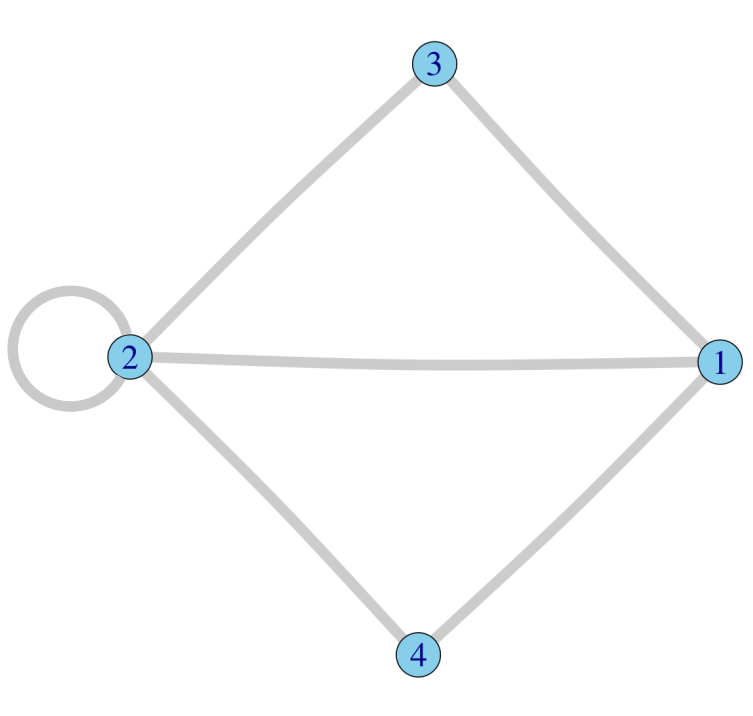
解 根据上面定义,得该图的邻接矩阵为,
注意,这里的一个环在算边数时只算 1。
图的邻接矩阵很好地刻画了图中各节点间的邻接关系,这很有用,但是这里不考虑这点。
我们来看看它作为矩阵,能不能让它参与运算呢?比如,矩阵乘法。我们知道,用矩阵表示线性变换的话,矩阵乘法可以表示变换的复合。
那么问题来了,邻接矩阵可以相乘吗?能的话,相乘又意味着什么呢?实际上,对于一个图,可以用它的邻接矩阵来确定两个节点之间的通路的数目。
我们直接看答案,邻接矩阵可以跟自己相乘,即幂次。
定理 设
证明 只看核心点,假设
.连通矩阵
两个节点间有通路相连则称两个节点连通,否则为不连通。
定义 设
用计算机求一个图的连通矩阵并不像求邻接矩阵那样方便,特别是对于比较复杂的图。这里我们给出一个借助于邻接矩阵来求连通矩阵的方法。
根据上面定理可知,对于如下矩阵之和
当
将矩阵
例子 求上文中那个带环图的连通矩阵。
解 上面已经给出了它的邻接矩阵,
先求出它的幂,然后再按上面的方法求连通矩阵。
最后得到如下连通矩阵,
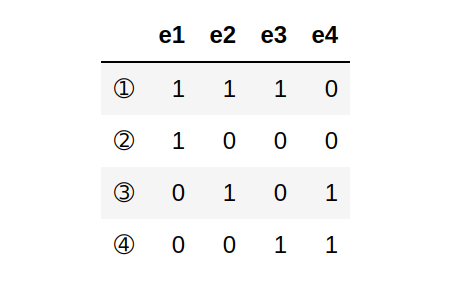
.关联矩阵(Incidence matrix)
定义 设
类似于邻接矩阵,关联矩阵依赖于
再次看上文中的带环图,它的关联矩阵如下,
其中边的次序为,
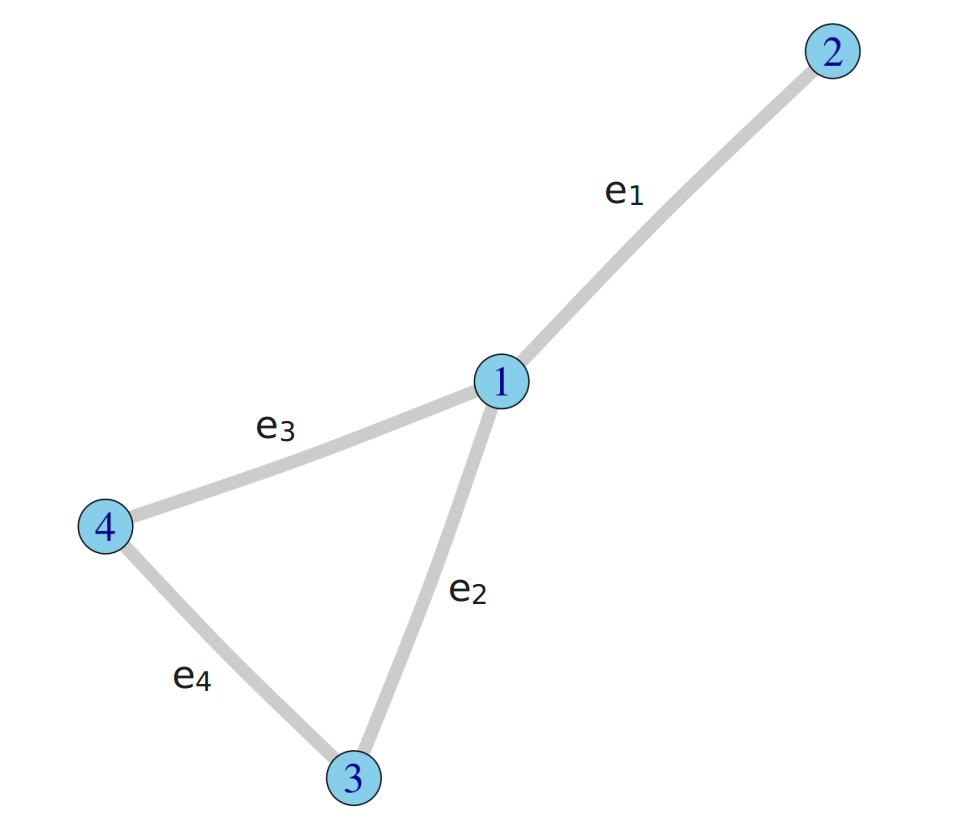
其关联矩阵为,
关联矩阵的行对应节点,列对应边。
.度矩阵(Degree matrix)
先看一个概念,即节点的度。节点
我们来看一下七桥问题中的图上节点的度,

图
例子 再次看上面那个带环图。

它的度矩阵为,
观察一下与邻接矩阵的关系,
发现邻接矩阵中对角线上的元素需要乘以 2,然后每行加起来就得到该行对应的节点的度。
.图拉普拉斯矩阵
对于没有环和平行边的简单图,可以如下定义图上的拉普拉斯矩阵,
即度矩阵减去邻接矩阵。

上面这个图的拉普拉斯矩阵为,
[,1] [,2] [,3] [,4]
[1,] 3 -1 -1 -1
[2,] -1 3 -1 -1
[3,] -1 -1 2 0
[4,] -1 -1 0 2
这里主要是展现用矩阵表示图的情况,关于图上拉普拉斯矩阵的更多内容留到后面。
4小结
矩阵可以表示图像(Image),也可以表示图(Graph),此时的矩阵并不像是变换的化身,算是矩阵的另一重身份。
有趣的是,矩阵表示图以后,有时候竟然也能参与矩阵乘法,请弄清楚该运算的意义。
此篇讲了用矩阵老哥表示图老弟的各种方式,下篇我们来看用图反过来表示矩阵。
