与 AI 博弈:从 AlphaGo 到 MuZero(一)
AlphaGo 论文地址:https://www.nature.com/articles/nature16961 AlphaGo Zero 论文地址:https://www.nature.com/articles/nature24270 AlphaZero 论文地址:https://arxiv.org/abs/1712.01815 MuZero 论文地址:https://arxiv.org/abs/1911.08265
DeepMind 官网介绍:https://deepmind.com/research/case-studies/alphago-the-story-so-far
0. 预备知识
信息对称( Perfect information / Fully information ):是指游戏的所有信息和状态都是所有玩家都可以观察到的,因此双方的游戏策略只需要关注共同的状态即可,而信息不对称(Imperfect information / Partial information)就是玩家拥有只有自己可以观察到的状态,这样游戏决策时也需要考虑更多的因素。
零和(zero-sum):就是所有玩家的收益之和为零,如果我赢就是你输,没有双赢或者双输,因此游戏决策时不需要考虑合作等因素。
纳什平衡(Nash equilibrium):又称为非合作博弈均衡,是博弈论的一个重要术语,以约翰·纳什命名。在一个博弈过程中,无论对方的策略选择如何,当事人一方都会选择某个确定的策略,则该策略被称作支配性策略。如果两个博弈的当事人的策略组合分别构成各自的支配性策略,那么这个组合就被定义为纳什平衡。
0.1 马尔可夫决策过程(Markov decision process,MDP)
基本的强化学习可以建模为马尔可夫决策过程:
环境状态的集合 ; 动作的集合 ; 在状态之间转换的规则(转移概率矩阵); 规定转换后“即时奖励”的规则(奖励函数); 描述主体能够观察到什么的规则;
规则通常是随机的。主体通常可以观察即时奖励和最后一次转换。在许多模型中,主体被假设为可以观察现有的环境状态,这种情况称为“完全可观测”(full observability),反之则称为“部分可观测”(partial observability)。通常,主体被允许的动作是有限的,例如,在棋盘中棋子只能上、下、左、右移动,或是使用的游戏金币不能多于所拥有的。
强化学习的主体与环境基于离散的时间步作用。在每一个时间 ,主体接收到一个观测 通常包含奖励 。然后它从合法的动作集合中选择一个动作 ,然后送到环境中去。环境则变化到一个新的状态 ,然后决定了这个变化 相关联的奖励 。
强化学习主体的目标,是得到尽可能多的奖励。主体选择的动作是其历史的函数,它也可以选择随机的动作。
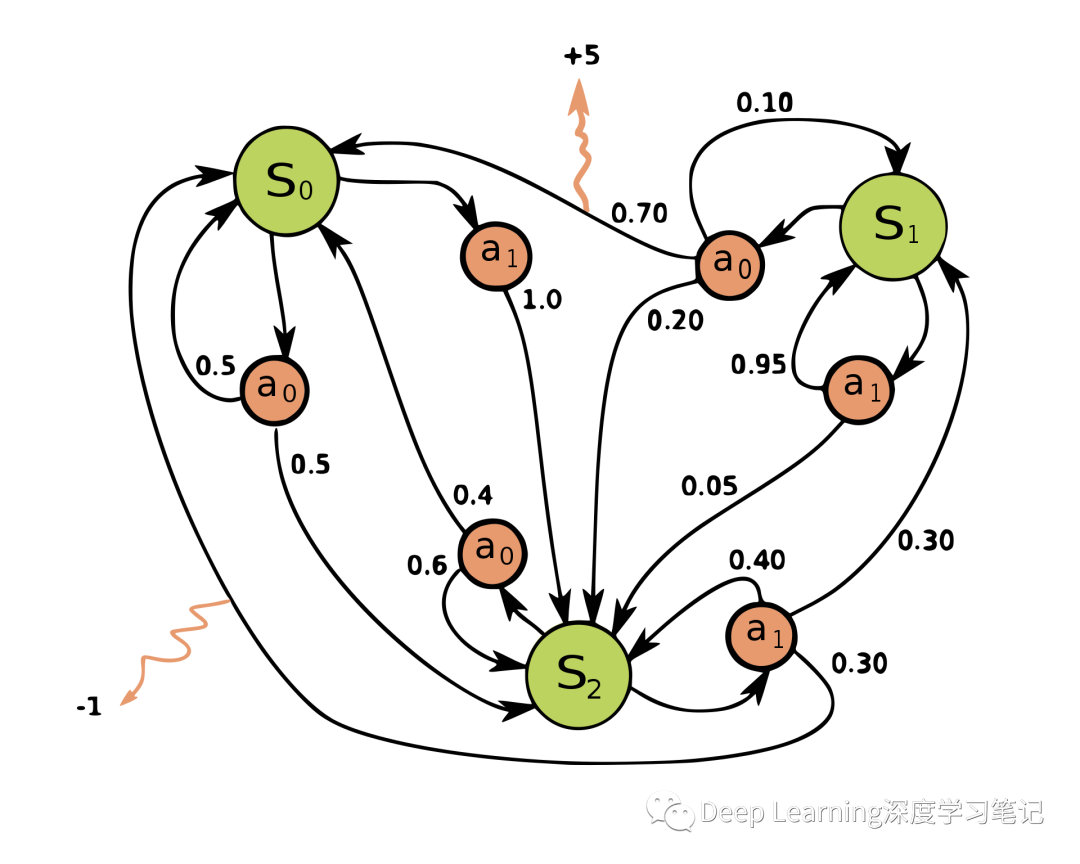 一个简单的 MDP 示例,包含三个状态(绿色圆圈)和两个动作(橙色圆圈),以及两个奖励(橙色箭头)
一个简单的 MDP 示例,包含三个状态(绿色圆圈)和两个动作(橙色圆圈),以及两个奖励(橙色箭头)
在每个时间步骤中,随机过程都处于某种状态 ,决策者可以选择在状态 下可用的动作 。该随机过程在下一时间步骤会随机进入新状态 ,并给予决策者相应的回馈 。
随机过程进入新状态 的概率受所选操作影响。具体来说,它是由状态转移函数 给出的。因此,下一个状态 取决于当前状态 和决策者的动作 。但是给定 和 ,它条件独立于所有先前的状态和动作;换句话说,MDP 的状态变换满足马尔可夫性质。
马尔可夫决策过程是马尔可夫链的推广,不同之处在于添加了行动(允许选择)和奖励(给予动机)。反过来说,如果每个状态只存在一个操作和所有的奖励都是一样的,一个马尔可夫决策过程可以归结为一个马尔可夫链。
0.2 围棋(Go Game)
标准国际围棋具有 个网格,共计 个点。
状态空间:由黑棋、白棋、空格组成
状态 可由 的张量表示,其值为 0 或 1。 初代 AlphaGo 采用 的张量表示。 动作空间:
可能的动作序列数为:
下棋时,对弈双方各执一种颜色的棋子,黑先白后,轮流将一枚棋子放置于交叉点上。与棋子直线相连的空白交叉点叫做气。当这些气都被对方棋子占据后,该棋子就没有了“气”,要被从棋盘上提掉。如果棋子的相邻(仅上下左右)直线交叉点上有了同色的棋子,则这两个棋子被叫做相连的。任意多个棋子可以以此方式联成一体,连成一体的棋子的气的数目是所有组成这块棋的单个棋子气数之和。如果这些气都被异色棋子占领,这块棋子就要被一起提掉。
在任何情况下,均禁止棋手向棋盘连下两子,否则将立刻判负。因此较文雅的中盘认输方法——投子,即是向棋盘摆下两枚棋子。
劫是围棋中较特殊的一种情况。举例来说,当黑方某一手提掉对方一子,而这一个黑子恰好处于白方虎口之内,这时白方不能立即提掉这一黑子,而必须在棋盘其他地方着一手(称为“找劫材”),使黑方不得不应一手(称为“应劫”),然后白才能够提掉这个黑子。故高手下棋常常会保留一些先手作为劫材,一旦形成打劫,劫材多的一方打胜的可能性较大。
0.2.1 Tromp-Taylor 规则
AlphaGo Zero 采用的围棋规则为 Tromp-Taylor 规则
围棋是在一个 的方格子上进行的,由两个叫黑方和白方的棋手进行。 网格上的每一个点都可以染色为黑色、白色或空三种颜色之一。 给定点 P ,如果没有被染色为 C ,且存在一条(水平或垂直)起始于 P 点、由相连的 P 的同色点组成、终止于某 C 色点的路径,那么我们说点 P 能到达 C 色。 清除一种颜色是指清空一切那种颜色且不能到达无色的点。 从全盘无色的格点开始,两位玩家轮流操作,由黑方先行。 每个回合,玩家只能从以下两种操作中选择其一:a. 弃权;b.行动;且此行动的结果不得重复已有的格点染色。 一次行动由以下步骤组成:a.将一个无色点染成己方的颜色; b.然后清除对方的颜色;c.清除己方的颜色。 游戏在连续两次弃权后结束。 黑(白)方的总分是黑(白)色格点颜色的总数,与仅与黑(白)色相连的无色点的总数之和。 游戏结束时,得分较高的玩家为胜者。分数相同则为平局。
0.3 蒙特卡洛树搜索(Monte Carlo Tree Search, MCTS)
蒙特卡洛树搜索的重点是分析最有希望的棋步,根据搜索空间的随机抽样来扩大搜索树。在每一次博弈中,通过随机选择棋步将游戏进行到最后。每次博弈的最终结果被用来给博弈树中的结点加权,以便在未来的博弈中更有可能选择更好的结点。博弈中最基本方法是在当前棋手的每一步可能的合法棋步之后应用相同数量的对局,然后选择最可能胜利的棋步。这种方法的称为朴素蒙特卡洛对局搜索( Pure Monte Carlo Game Search),其效率通常会随着时间的推移而增加,因为根据以前的对局,更多的对局被分配给最能让当前棋手胜利的棋步。每一轮蒙特卡洛树搜索包括四个步骤:
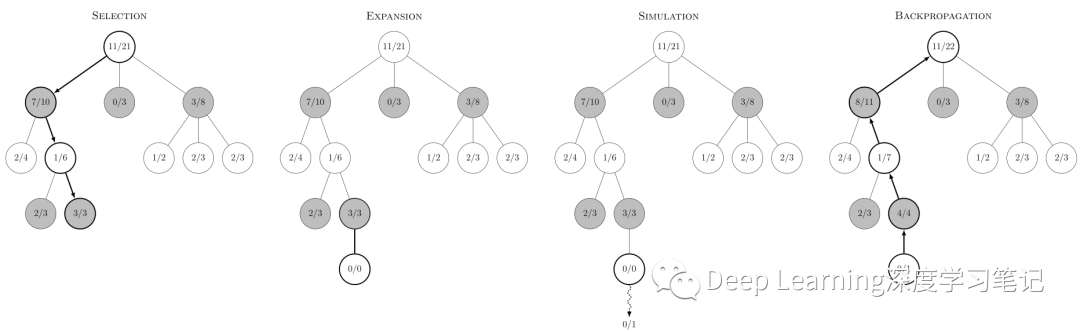 上图显示了一个决策所涉及的步骤,每一个结点的内容代表胜利次数/游戏次数。在选择中,黑色即将移动。根节点显示,到目前为止,在这个位置的 21 场白棋有 11 场获胜。它也反映出了沿其下方三个黑色节点显示的总共 10/21 黑色胜利,每个黑色节点代表一个可能的黑色移动。如果白色输掉了模拟,则选择步骤所有结点都会增加它们的模拟计数(分母加一),但黑色结点由于获得胜利其分子加一。如果相反,白色获胜,则选择中的所有结点仍将增加其模拟计数(分母加一),但其中由于白色节点将获得胜利其分子加一。在可以平局的游戏中,平局会导致黑色和白色的分子增加 0.5,分母增加 1。这确保了在选择步骤期间,每个玩家的选择扩展到该玩家最有可能的移动,也反映了每个玩家的目标是最大化他们移动的价值。
上图显示了一个决策所涉及的步骤,每一个结点的内容代表胜利次数/游戏次数。在选择中,黑色即将移动。根节点显示,到目前为止,在这个位置的 21 场白棋有 11 场获胜。它也反映出了沿其下方三个黑色节点显示的总共 10/21 黑色胜利,每个黑色节点代表一个可能的黑色移动。如果白色输掉了模拟,则选择步骤所有结点都会增加它们的模拟计数(分母加一),但黑色结点由于获得胜利其分子加一。如果相反,白色获胜,则选择中的所有结点仍将增加其模拟计数(分母加一),但其中由于白色节点将获得胜利其分子加一。在可以平局的游戏中,平局会导致黑色和白色的分子增加 0.5,分母增加 1。这确保了在选择步骤期间,每个玩家的选择扩展到该玩家最有可能的移动,也反映了每个玩家的目标是最大化他们移动的价值。
蒙特卡洛搜索具体步骤:
[1] 选择(Selection):从根结点 出发递归选择连续的子结点直到到达叶子结点 ( Tree Policy 为选择结点(落子)的策略,它的好坏直接影响搜索的好坏,所以是 MCTS 的一个研究重点。选择平均赢子数最多的走法就是一种 Tree Policy,而目前采用最广泛的策略有 UCT)。根结点为当前游戏状态,而叶子结点为任何潜在(没有进行模拟)的合法下一步操作。下面的步骤是一种偏向于选择子结点的方法,它让游戏树向最有希望的棋步扩展,这是蒙特卡洛树搜索的本质。
对于被检查的结点( 假设 Tree Policy 为 UCT 算法),它有三种可能:
该结点所有的动作都已经被扩展过:那么将使用 UCB 公式计算该节点所有子节点的 UCB 值,并找到值最大的一个子结点继续检查。反复向下迭代。执行步骤 [1] 该结点有可行的动作还未被扩展过:如果被检查的棋局依然存在没有被拓展的子节点(例如说某结点有 20 个可行动作,但是在搜索树中才创建了 19 个子节点),那么认为这个结点就是本次迭代的的目标结点 ,并找出 还未被拓展的动作 。执行步骤 [2] 选择该结点时游戏已经结束:直接执行步骤 [4] [2] 扩展(Expansion):创建结点 一个或多个子结点并从中选择结点 。 的棋局就是结点 在执行了动作 之后的棋局。
[3] 模拟(Simulation):在结点 开始,根据 Default Policy 从扩展的位置模拟下棋到终局,计算节点 的质量度。完全随机落子就是一种最简单的 Default Policy。当然完全随机是比较低效的,通过加上一些先验知识等方法改进这一部分能够更加准确的估计落子的价值,增加程序的棋力。Default Policy 可以使用深度学习网络,比如 AlphaGo Zero。
[4] 反向传播(Backpropagation):使用随机游戏的结果,更新从 到 的路径上的结点信息
0.4 UCT(Upper Confidence Bounds for Tree)
UCT 的全称是 UCB for Trees,UCB 指的是 Upper Confidence Bounds。
首先,提出一个多臂老虎机问题(The Multi-Armed Bandit Problem)
多臂老虎机是一个有多个拉杆的赌博机,每一个拉杆的中奖几率是不一样的,问题是:如何在有限次数内,选择拉不同的拉杆,获得最多的收益。假设这个老虎机有 5 个拉杆,最简单的方法就是每个拉杆都试几次,找到中奖概率最大的那个拉杆,然后把之后有限的游戏机会都用在这个拉杆上。然而这个方法并不是可靠的,因为每个拉杆试 1000 次显然比试 10 次所获得的中奖概率(预估概率)更加准确。比如你试了10次,其中那个本来中奖概率不高的拉杆,有可能因为你运气好,会给你一个高概率中奖的假象。在有限次数下,你到底是坚持在你认为中奖概率高的拉杆上投入更多的次数呢( Exploit ),还是去试试别的拉杆( Explore )呢?如何分配 Explore 和 Exploit 的次数?
很明显最优的策略(optimal policy)为每次均选择最高中奖概率的拉杆,但这明显这种方式是不切实际的。必须花费一部分时间去寻找最高中奖率的拉杆。因此需要使用其他策略去接近最优策略。
就最大限度地提高总回报而言,一个更好的方式是将一段时间内的采样限制在表现最好的行动上。这正是置信度上限(UCB)策略所采取的方法。
0.4.1 The Upper Confidence Bound (UCB) Algorithm
UCB 算法不是通过简单地选择一个任意的行动来进行探索(exploration),并且选择的概率保持不变,而是在收集更多的环境知识时改变其 exploration-exploitation 的平衡。其移动主要聚焦于 exploration,当那些被试得最少的行动被优先考虑时,就会专注于 exploitation,选择具有最高估计回报的动作。
UCB 算法中, 表示在时间步 下的动作选择:
其中:
为动作 在时间步 的价值估计 为动作 在时间步 之前被选择过的次数 为控制 exploration 程度的置信值
UCB 公式可以被认为是由两个不同的部分组成:
Exploitation: 代表代表方程的 exploitation 部分。UCB是基于 "在不确定的事实中保持乐观 "的原则,这基本上意味着如果不知道哪个行动是最好的,那么就选择目前看起来是最好的行动。等式的这一半本身就能做到这一点:目前具有最高估计回报的行动将是被选择的行动。 Exploration: 方程的后半部分增加了 exploration ,探索的程度由超参数 调整。有效地,方程的这一部分提供了对行动奖励估计的不确定性的测量。 如果一个动作没有被经常尝试,或者根本没有被尝试,那么 就会很小。因此,不确定性项会很大,使这个动作更有可能被选中。每采取一次动作,就会对其估计值更有信心。在这种情况下, 递增,因此不确定性项减少,使得这个行动作为探索的结果被选择的可能性降低(尽管由于 exploitation 部分,它仍然可能被选为具有最高价值的行动)。 当没有选择某个动作时,其不确定性项将缓慢增长,这是由于分子中的对数函数。然而,每选择该动作时,由于 的增加是线性的,不确定性将迅速缩小。因此,由于奖励估计的不确定性,对于不经常选择的操作,exploration 部分会更大。 随着时间的推移,exploration 部分逐渐减少(因为当 到无限大时,因为 ),直到最终只根据 exploitation 来选择行动。
1. AlphaGO

AlphaGo 是一个玩棋盘游戏的计算机程序。它由 Google(现为 Alphabet Inc.)的子公司 DeepMind Technologies 开发。AlphaGo 的后续版本变得越来越强大,包括以 Master 为名的版本。在退出竞技比赛后,AlphaGo Master 被称为 AlphaGo Zero 的更强大版本接替,它完全是无监督训练得到,没有从人类游戏经验中学习。AlphaGo Zero 随后被推广到一个名为 AlphaZero 的程序中,该程序可以玩其他游戏,包括国际象棋和将棋。AlphaZero 又被一个名为 MuZero 的程序所取代,该程序无需学习规则即可学习。
简单来说,AlphaGo 的做法是使用了蒙特卡洛树搜索与两个深度神经网络相结合的方法,一个是通过估值网络(value network)来评估大量的选点,一个是通过策略网络(policy network)来选择落子,并使用强化学习进一步改善它。在这种设计下,电脑可以结合树状图的长远推断,又可像人类的大脑一样自发学习进行直觉训练,以提高下棋实力。
| 版本 | 硬件资源 | Elo rating | 日期 | 成绩 |
|---|---|---|---|---|
| AlphaGo Fan | 176 GPUs | 3,144 | Oct 2015 | 5:0 against Fan Hui |
| AlphaGo Lee | 48 TPUs distributed | 3,739 | Mar 2016 | 4:1 against Lee Sedol |
| AlphaGo Master | 4 TPUs,single machine | 4,858 | May 2017 | 60:0 against professional players; Future of Go Summit |
| AlphaGo Zero (40 block) | 4 TPUs,single machine | 5,185 | Oct 2017 | 100:0 against AlphaGo Lee89:11 against AlphaGo Master |
| AlphaZero (20 block) | 4 TPUs, single machine | 5,018 | Dec 2017 | 60:40 against AlphaGo Zero (20 block) |
1.1 AlphaGo 历史
AlphaGo 的研究计划于 2014 年启动,此后和之前的围棋程序相比表现出显著提升。在和 Crazy Stone 和 Zen 等其他围棋程序的500局比赛中,单机版 AlphaGo(运行于一台电脑上)仅输一局。而在其后的对局中,分布式版AlphaGo(以分布式运算运行于多台电脑上)在 500 局比赛中全部获胜,且对抗运行在单机上的 AlphaGo 约有77% 的胜率。2015年 10 月的分布式运算版本 AlphaGo 使用了 1,202 块 CPU 及 176 块 GPU。
2015 年 10 月,AlphaGo 击败樊麾,成为第一个无需让子即可在 19 路棋盘上击败围棋职业棋手的电脑围棋程序,写下了历史,并于 2016 年 1 月发表在知名期刊《自然》。
2016 年 3 月,透过自我对弈数以万计盘进行练习强化,AlphaGo 在一场五番棋比赛中 4:1 击败顶尖职业棋手李世石,成为第一个不借助让子而击败围棋职业九段棋手的电脑围棋程序,立下了里程碑。五局赛后韩国棋院授予 AlphaGo 有史以来第一位名誉职业九段。
2016 年 7 月 18 日,因柯洁那段时间状态不佳,其在 Go Ratings 网站上的 WHR 等级分下滑,AlphaGo 得以在 Go Ratings 网站的排名中位列世界第一,但几天之后,柯洁便又反超了 AlphaGo。2017 年 2 月初,Go Ratings 网站删除了 AlphaGo、DeepZenGo 等围棋人工智能在该网站上的所有信息。
2016 年 12 月 29 日至 2017 年 1 月 4 日,再度强化的 AlphaGo 以 “Master” 为账号名称,在未公开其真实身份的情况下,借非正式的网络快棋对战进行测试,挑战中韩日的一流高手,测试结束时 60 战全胜。
2017 年 5 月 23 至 27 日在乌镇围棋峰会上,最新的强化版 AlphaGo 和世界第一棋手柯洁比试、并配合八段棋手协同作战与对决五位顶尖九段棋手等五场比赛,获取三比零全胜的战绩,团队战与组队战也全胜,此次AlphaGo 利用谷歌 TPU 执行,加上快速进化的机器学习法,运算资源消耗仅李世石版本的十分之一。在与柯洁的比赛结束后,中国围棋协会授予 AlphaGo 职业围棋九段的称号。
AlphaGo 在没有人类对手后,AlphaGo 之父杰米斯·哈萨比斯宣布 AlphaGo 退役。而从业余棋手的水平到世界第一,AlphaGo 的棋力获取这样的进步,仅仅花了两年左右。
AlphaGo Zero 拥有更加强大的学习能力,可自我学习,在 21 天达到胜过中国顶尖棋手柯洁的 Alpha Go Master 的水平。
DeepMind 后来开发了 AlphaZero,这是 AlphaGo Zero 的通用版本,除了围棋之外,它还可以下国际象棋和将棋。2017 年 12 月,AlphaZero 以 60 比 40 的胜负击败了 3 天版的 AlphaGo Zero,并且经过 8 小时的训练,它在 Elo 等级上的表现超过了 AlphaGo Lee。AlphaZero 还击败了顶级国际象棋程序 (Stockfish) 和顶级将棋程序 (Elmo)。
1.2 AlphaGo 公开模型迭代

2. AlphaGo
AlphaGo 是该系列的第一篇论文,展示了深度神经网络可以通过预测策略(从状态到行动的映射)和价值估计(从给定状态获胜的概率)来进行围棋。这些策略和价值网络被用来加强基于树的搜索,通过选择从给定状态中采取哪些行动,以及哪些状态值得进一步探索。
AlphaGo 使用 4 个深度卷积神经网络:3 个策略网络和 1 个价值网络。其中 2 个策略网络通过人类历史棋局中的走法进行监督学习训练。
监督学习描述了由多种损失函数 组成的损失函数。在这种情况下, 是策略网络从一个给定的状态预测的动作,而 是人类玩家在该状态下采取的行动。
Rollout policy 是一个较小的神经网络,它也接受较小的输入状态表示。因此,与更高容量的网络相比, rollout policy 对人类高手走法的建模精度要低得多。然而, rollout policy 网络的推理时间(在给定状态下预测动作的时间)为 2 微秒,而较大的网络为 3 毫秒,这使其对蒙特卡洛树搜索模拟非常有用。
作者使用由多个机器学习阶段组成的管道来训练神经网络。首先直接从围棋专家的棋局动作中训练一个监督学习 (SL) 策略网络 。这提供了具有即时反馈和高质量梯度的快速、高效的学习更新。作者还训练了一个快速策略 ,它可以在 Rollout 期间快速采样动作。接下来,作者训练强化学习 (RL) 策略网络 ,通过优化自我博弈的最终结果来改进 SL 策略网络。这会将策略调整到赢得比赛的正确目标,而不是最大限度地提高预测准确性。最后,作者训练了一个价值网络 来预测 RL 策略网络自我博弈的赢家。AlphaGo 有效地将策略和价值网络与 MCTS 相结合。
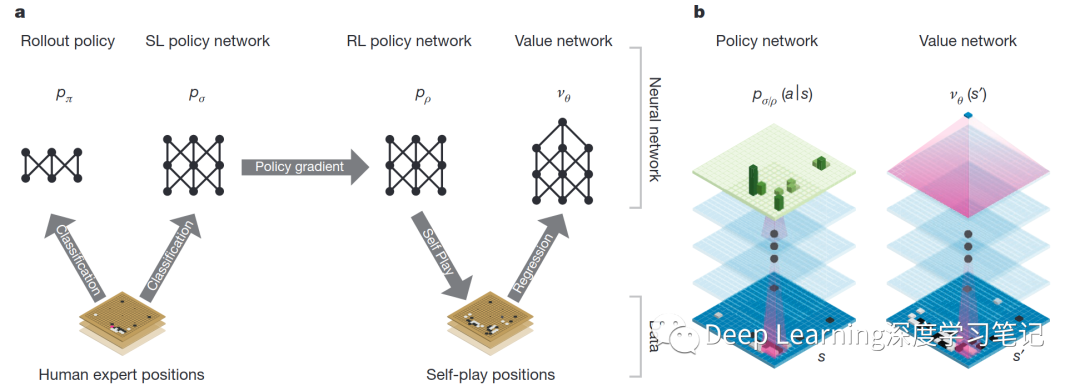 神经网络训练管道以及架构 a.训练快速 Rollout 策略网络 和监督学习 (SL) 策略网络 以预测人类围棋专家在棋局数据集中的移动。强化学习 (RL) 策略网络 被初始化为 SL 策略网络,然后通过策略梯度学习进行改进,以最大化结果(即赢得更多游戏)与先前版本的策略网络相比。通过使用 RL 策略网络玩自我博弈来生成一个新的数据集。最后,通过回归训练一个价值网络 ,以预测来自自我博弈数据集的位置的预期结果(即当前玩家是否获胜)。b. AlphaGo 中使用的神经网络架构的示意图。策略网络将棋盘位置 的表示作为其输入,通过参数为 (SL 策略网络)或 (RL 策略网络)的许多卷积层,并输出 或 合法动作 的概率分布,由棋盘上的概率图表示。价值网络类似地使用参数为 的卷积层,但输出一个标量值 来预测位置 的预期结果。
神经网络训练管道以及架构 a.训练快速 Rollout 策略网络 和监督学习 (SL) 策略网络 以预测人类围棋专家在棋局数据集中的移动。强化学习 (RL) 策略网络 被初始化为 SL 策略网络,然后通过策略梯度学习进行改进,以最大化结果(即赢得更多游戏)与先前版本的策略网络相比。通过使用 RL 策略网络玩自我博弈来生成一个新的数据集。最后,通过回归训练一个价值网络 ,以预测来自自我博弈数据集的位置的预期结果(即当前玩家是否获胜)。b. AlphaGo 中使用的神经网络架构的示意图。策略网络将棋盘位置 的表示作为其输入,通过参数为 (SL 策略网络)或 (RL 策略网络)的许多卷积层,并输出 或 合法动作 的概率分布,由棋盘上的概率图表示。价值网络类似地使用参数为 的卷积层,但输出一个标量值 来预测位置 的预期结果。
2.1 Supervised Learning of Policy Networks
对于训练的第一阶段,作者建立在先前的工作之上,即使用监督学习预测围棋游戏中的围棋专家移动。SL 策略网络 为权重为 的卷积层和激活函数的组合。最终的 层输出所有合法动作 的概率分布。策略网络的输入 是棋局状态的简单表示。策略网络在随机采样的状态-动作对 上进行训练,使用随机梯度上升法来最大化在状态 中选择的人类动作 的可能性,
作者从 KGS 围棋服务器的 3000 万个棋局中训练了一个 13 层的策略网络,并称之为 SL 策略网络。该网络在测试集上预测人类围棋专家的走法,使用所有输入特征的准确率为 57.0%,仅使用原始棋盘位置和移动历史作为输入的准确率为 55.7%。准确率的小幅提高导致了棋力的大幅提高;更大的网络能达到更好的准确率,但在搜索过程中评估起来比较慢。作者还训练了一个更快但不太准确的 rollout 策略网络 ,使用权重为 的小模式特征的线性 ;这达到了 24.2% 的准确率,只用了 2μs 来选择一个动作,而不是策略网络的 3ms。
2.2 Reinforcement learning of policy networks
训练的第二阶段旨在通过策略梯度强化学习 (RL) 来改进策略网络。RL 策略网络 在结构上与 SL 策略网络相同,并且其权重 被初始化为相同的值:。作者在当前策略网络 和随机选择先前迭代的策略网络之间进行博弈。随机选择先前迭代的策略网络作为对手可以通过防止过度拟合当前策略来稳定训练。使用奖励函数 ,对于所有非终局时间步 ,该函数值为零。结果 是从当前角度来看游戏结束时的终局奖励在时间步 的玩家: 表示获胜, 表示失败。然后通过随机梯度上升法在每个时间步 更新权重,其方向是使预期结果最大化:
作者评估了 RL 策略网络在游戏中的性能,从动作的输出概率分布中以 对每个动作进行采样。当正面交锋时,RL 策略网络在与 SL 策略网络的比赛中胜率超过 80%。作者还针对当时最强大的开源围棋程序 Pachi 进行了测试(这是一个复杂的蒙特卡洛搜索程序,在 KGS 上排名第 2 位,每步执行 100,000 次模拟。完全不使用搜索)RL 策略网络赢得了与 Pachi 的 85% 的比赛。
2.3 Reinforcement Learning of Value Networks
训练的最后阶段侧重于位置评估,估计一个价值函数 ,该函数预测双方使用政策 p 进行游戏的位置 s 的结果:
理想情况下,想知道完美玩法下的最优价值函数 ;在实践中,作者使用 RL 策略网络 来估计策略的价值函数 。使用权重为 的价值网络 来近似价值函数,。该神经网络具有与策略网络类似的架构,但输出的是单个预测而不是概率分布。作者通过状态-结果对 的回归来训练价值网络的权重,使用随机梯度下降来最小化预测值 与相应结果 之间的均方误差 (MSE)
**从包含完整游戏的数据中预测游戏结果的朴素方法会导致过度拟合。**问题是连续的位置是强相关的,仅仅相差一子,但回归目标是为整个游戏共享的。当以这种方式在 KGS 数据集上进行训练时,价值网络记住了游戏结果,而不是推广到新的位置,在测试集上实现了 0.37 的最小 MSE,而在训练集上为 0.19。为了缓解这个问题,作者生成了一个新的自我对弈数据集,其中包含 3000 万个不同的位置,每个位置都从一个单独的游戏中采样。每个游戏都在 RL 策略网络和自身之间进行,直到游戏结束。对该数据集的训练导致训练和测试集的 MSE 分别为 0.226 和 0.234。与使用快速 rollout 策略 的蒙特卡洛 rollout 相比;价值函数始终更准确。使用 RL 策略网络 对 的单一评估也接近了 Monte-Carlo rollouts 的准确性,但使用的计算量减少了 15,000 倍
2.4 Searching with policy and value networks
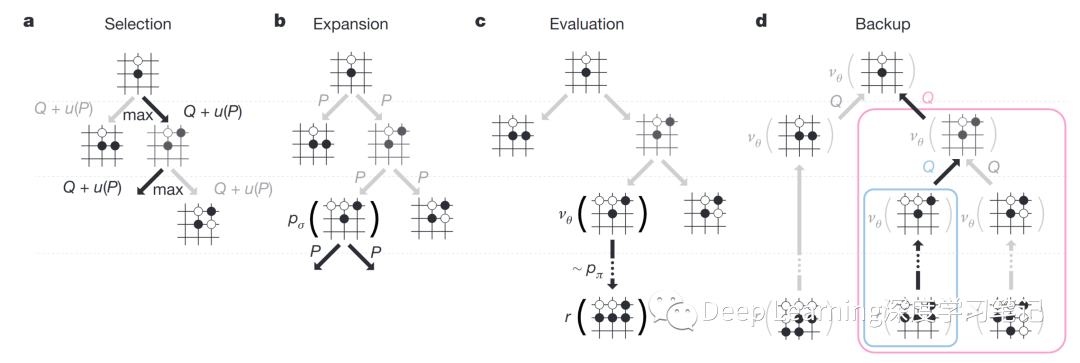 AlphaGo 中的蒙特卡洛树搜索。a.每次模拟通过选择具有最大动作值 的边以及取决于存储的该边的先验概率 的奖励 来遍历树。b.叶子节点可以展开;新节点由策略网络 处理一次,输出概率存储为每个动作的先验概率 。c.在模拟结束时,叶节点以两种方式评估:使用价值网络 ;并通过使用快速推出策略 将推出运行到游戏结束,然后使用函数 计算获胜者。d,更新动作值 以跟踪该动作下方子树中所有评估 和 的平均值
AlphaGo 中的蒙特卡洛树搜索。a.每次模拟通过选择具有最大动作值 的边以及取决于存储的该边的先验概率 的奖励 来遍历树。b.叶子节点可以展开;新节点由策略网络 处理一次,输出概率存储为每个动作的先验概率 。c.在模拟结束时,叶节点以两种方式评估:使用价值网络 ;并通过使用快速推出策略 将推出运行到游戏结束,然后使用函数 计算获胜者。d,更新动作值 以跟踪该动作下方子树中所有评估 和 的平均值
AlphaGo 在 MCTS 算法(上图)中结合了策略和价值网络,该算法选择步骤通过前瞻搜索。搜索树的每条边 存储一个动作价值 、访问计数 和先验概率 。树的遍历通过模拟,从根状态开始。在每个模拟的每个时间步 ,从状态 中选择一个动作 ,
以便最大化动作价值加上 与先验概率成正比,但随着重复访问而衰减以鼓励探索。当遍历在步骤 到达叶节点 时,叶节点可能被扩展。叶位置 仅由 SL 策略网络 处理一次。输出概率存储为每个合法动作 的先验概率 ,。叶节点以两种截然不同的方式进行评估:首先,通过价值网络 ;其次,通过使用快速 Rollout 策略 进行的随机 Rollout 的结果 直到最终步骤 ;使用混合参数 将这些评估组合成叶评估 ,
在模拟 结束时,更新所有遍历边的动作价值和访问计数。每条边都会累积通过该边的所有模拟的访问次数和平均评估,
其中 是第 次模拟的叶节点, 表示在第 次模拟期间是否遍历了边 。搜索完成后,算法从根位置选择访问次数最多的移动。
SL 策略网络 在 AlphaGo 中的表现优于更强的 RL 策略网络 ,作者推测是因为人类围棋专家选择了一系列有希望的移动,而 RL 优化了单一的最佳移动。然而,从更强的 RL 策略网络导出的值函数 在 AlphaGo 中的表现比从 SL 策略网络导出的值函数 更好。
评估策略和价值网络需要比传统搜索启发式多几个数量级的计算。为了有效地将 MCTS 与深度神经网络相结合,AlphaGo 使用异步多线程搜索,在 CPU 上执行模拟,并在 GPU 上并行计算策略和价值网络。AlphaGo 的最终版本使用了 40 个搜索线程、48 个 CPU 和 8 个 GPU。作者还实现了一个分布式版本的 AlphaGo,它利用了多台机器、40 个搜索线程、1202 个 CPU 和 176 个 GPU。
参考资料
http://tromp.github.io/go.html https://towardsdatascience.com/the-upper-confidence-bound-ucb-bandit-algorithm-c05c2bf4c13f https://en.wikipedia.org/wiki/AlphaGo https://deepmind.com/blog/article/alphago-zero-starting-scratch https://towardsdatascience.com/the-evolution-of-alphago-to-muzero-c2c37306bf9
