MIT和亚马逊举办的路径优化比赛—— US$175000的解决方案分享
MIT和亚马逊举办的路径优化比赛——
US$175000的解决方案分享
不久前
MIT和亚马逊联合举办的
最后一公里配送的路径优化比赛结束了(点击阅读全文,查看比赛链接)
前三名总共获得US$175000。
今天小编借着这个比赛的机会给大家介绍下相关的运筹优化知识和各路高手的解法。

目录/contents
1. 比赛简介
问题背景
数据集结构
成绩评价
2. 前3名的解决方案简介
第1名
第2名
第3名
3. 第1名的解决方案及细节分析
模型
具体求解步骤
(1)先将ATSP转化为TSP
(2)用zone-id得到cluster
(3)从历史数据得到软约束
对于step2 通过深度优先搜索将有向图变成 palm tree 结构
对于step3 从palm tree得到强连通分量 以及 分量路径
(4)用改进后的LKH-3求解
结果
题外话环节
参考资料
比赛简介
问题背景
最后一公里配送问题,指的就是区域配送中心到末端设施这一段的配送问题。司机需要在配送中心装载好货物,按顺序访问多个末端设施进行收货或送货操作,最后回到配送中心。
这个送货的路径在比赛中被称作route(如下图所示);配送中心是这条route的起点和终点,称做station;访问的末端设施,收件人寄件人的具体地址则被称作stop(图中圆点);图中stop的颜色相同说明归属于同一个zone;图中stop的标号说明访问这个stop的次序;而我们需要确定的就是这个次序,即stop sequence。
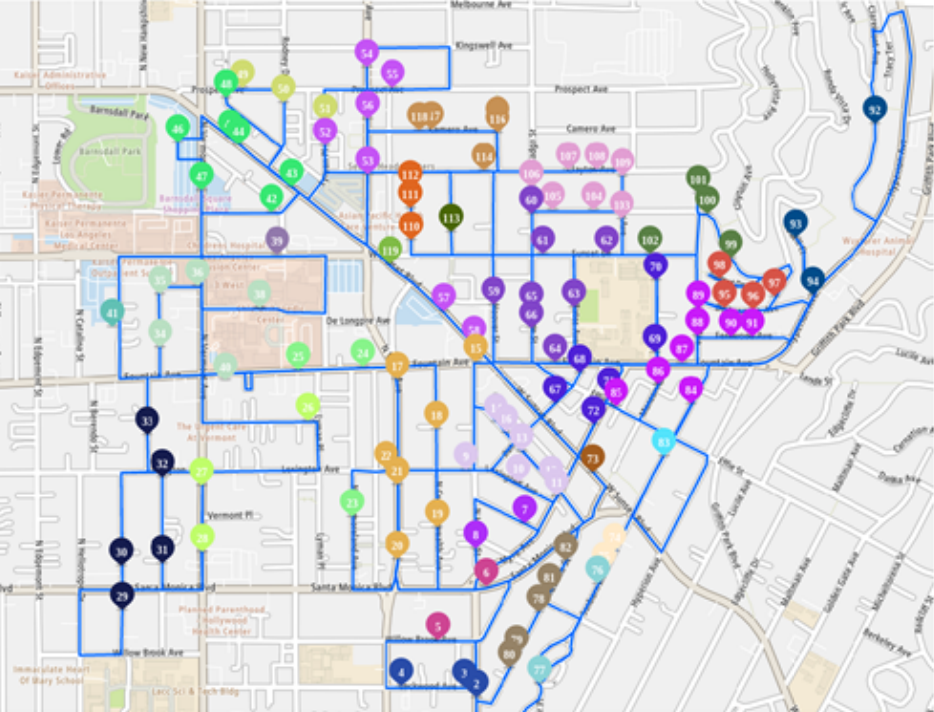
数据集结构
详见,官方data_structures文档
https://github.com/MIT-CAVE/rc-cli/blob/main/templates/data_structures.md
主要是
· route的实际stop sequence
· route的信息(如出发时间、日期、出发地点等)
· stop的信息(如stop的经纬度,是否送货,stop所属的zone id等)
· package的信息(如包裹的大小、包裹规定送达的时间窗等)
· stop之间的travel time
成绩评价
而如何评价一个sequence的好坏呢?这就是这个最后一公里问题不同寻常的地方了。不同于传统路径规划问题中配送距离或时间越短则说路径越好,而这里的路径好坏是人为评分的结果,分为高中低三个档次,这里可能包含了司机的主观经验。
故举办方会提供历史上6112条route的信息,其中有2718条评分高的route。参赛者在测试算法效果时,可将每条评分高的route的信息(如访问的stop的经纬度位置、包裹的尺寸等)输入算法中,输出每条route预测的stop sequence。通过计算预测的和实际的sequence间的相似程度,可以衡量算法预测出来的sequence的好坏。对所有的route重复上述操作即可获得总得分submission score,进而衡量算法的好坏。流程如下图所示:
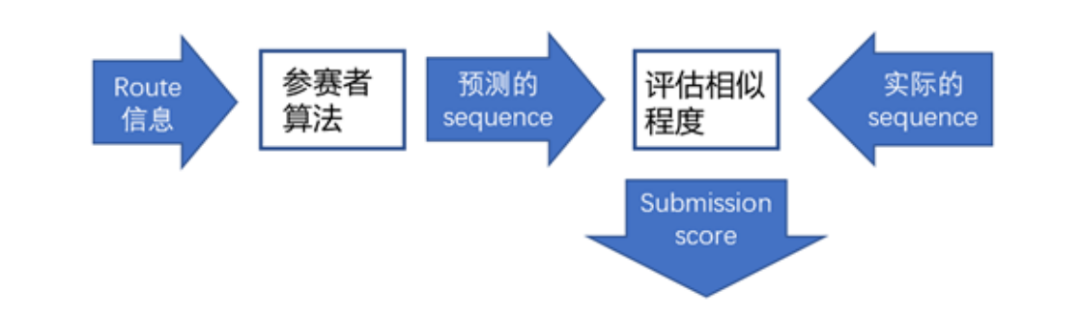
参赛者提交完最终版算法之后,举办方将输入的route替换成3000条新的route,重复上图流程后,根据得到的submission score对所有队伍由低到高进行排名。具体的计算方式如下式所列:
submission score 越低越好

这里举个栗子,如下表,序列A为依次访问站点1、2、3、4,序列B为依次访问站点2、4、3、1,则a[i]为B[i]在A中的位置,当a中的元素不严格按照升序排列,即A和B为相同序列时SD(A,B)会大于0,否则为0;SD(A,B)越大,说明A和B的差异越大。ERPnorm(A,B)表示的是A和B每位间的正则化行程距离,ERPe(A,B)表示A转换成B需要的最少操作数,即把3放在4前面,把1放在2前面共两次操作。ERPnorm(A,B)/ERPe(A,B)表示平均每次ERP操作所涉及的两个站点之间的正则化行程时间。
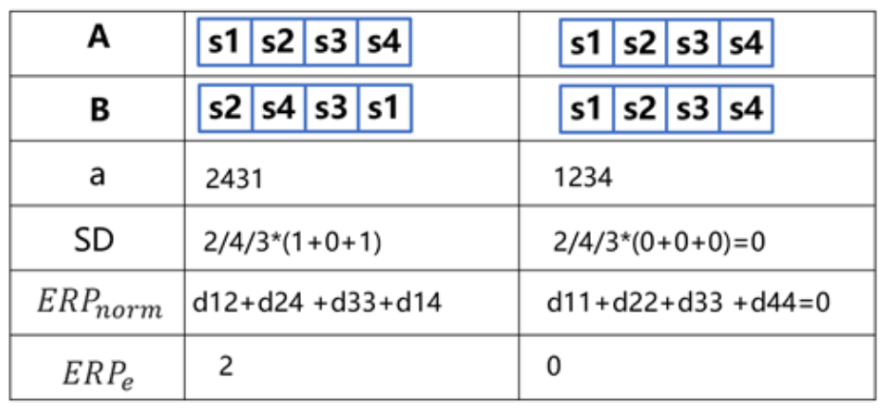
小知识:编辑距离
字符串的编辑距离,通常用来衡量两个字符串的差异化程度。最常见的编辑距离是Levenshtein距离,由俄罗斯的数学家Vladimir Levenshtein在1965年提出。是指利用字符操作,把字符串A转换成字符串B所需要的最少操作数。其中,字符操作包括:删除一个字符、插入一个字符、修改一个字符。一般来说,两个字符串的编辑距离越小,则它们越相似。
例如对于字符串 if 和 iff ,可以通过插入一个 f 或者删除一个'f'来达到目的。
总的来说,就是将实际的sequence作为一个最高基准,参赛方根据已有的信息预测的sequence和实际sequence越接近,说明其算法越好。虽说和机器学习很像,但遗憾的是,这次比赛中排行榜前三的队伍都是采用优化算法来求解的,接下来就给大家介绍一下~
前3名的解决方案简介
第1名
Local Search with Learned Constraints for Last Mile Routing
该篇文章将原始问题建模成带约束的非对称旅行商问题。具体的约束从历史数据中学得,主要包括簇约束、优先级约束。最后采用改进的LKH算法进行求解。
第2名
Last-Mile Delivery Trajectory Prediction Using Hierarchical TSP with Customized Cost Matrix
该篇文章将原始问题建模成多层次TSP问题(高层次将zone作为TSP中的城市,低层次的将stop作为TSP中的stop),并自定义成本矩阵(主要根据zone的层级关系调整行驶时间矩阵),分层次调用GLPK进行求解,最后对得到的sequence进行修正(根据历史数据判断是否需要将sequence翻转,即A->B->C变为C->B->A) 。
第3名
Data-Driven Vehicle Routing in Last-Mile Delivery
该篇文章也是将原始问题建模成TSP问题,不过它通过对历史数据的描述性分析,用zone_id来调整成本矩阵,直接调用遗传算法求解,然后调整超参数,得到最优模型后,再求得stop sequence。
第1名的解决方案及细节分析
Cook, W等人用此解决方案获得了第1名
也拿到了US$100,000,(羡慕🤑
模 型
目标函数:时间 + 惩罚系数*软约束的惩罚
硬约束:
簇约束(cluster constraint): stop只能与相同cluster的stop进行拼接
硬约束(hard-constraint):在任何时候都必须满足的约束
cluster指的是根据某种规则将stop聚类得到的。文中多次聚类得到 cluster, super cluster, super-super cluster, top-level cluster 如无特殊说明,后续用 cluster 指代这4种
软约束:
优先级约束(precedence constraint): stop(或cluster)之间有先后顺序。e.g. : precedence(a,b) a必须在b之前先访问。
路径约束(path constraint): stop(或cluster)之间有先后顺序,并且相连。e.g.:path(a,b) 访问a后必须马上访问b。
邻居约束(neighbor constraint): stop(或cluster)之间必须相连。e.g.:path(a,b) a必须是b的上一个或下一个。
软约束(soft-constraint):一种尽可能满足的“希望”
原文中还考虑了一种软约束,称为binary disjunction,是针对以上3种约束而建立的另一个约束。例如,binary disjunction(A,B)表示模型中同时考虑约束A或约束B,满足其一即可避免惩罚
具体求解步骤
(1)先将ATSP转化为TSP
可以参见往期的文章
非对称TSP问题(Asymmetric Travelling Salesman Problem)转换为对称TSP问题
https://mp.weixin.qq.com/s/Df5CxbK4bVgTTIVbTZHWSg
(2)用zone-id得到cluster
一个stop是带有 zone-id 属性的,该属性与实际sequence有很大的联系,往往同一个zone下stop访问完了,才会访问下一个zone。
大部分参赛队伍都通过分析历史数据知道了这点,并且以此来作为改进TSP求解的一个重点
一个zone-id由4部分组成 [符号]-[数字].[数字][符号] ,例如 A-2.2E ,所以作者根据以此得到4种层级的cluster。比如4部分都相同的为最底层的cluster。super-cluster则有3部分相同,例如 A-2.2[符号] 与 A-2.2E 是属于同一个 super-cluster 。以此类推
(3)从历史数据得到软约束
这里是小编认为文章最精彩的部分,也是其与众不同之处。限于篇幅,这里仅以最底层的cluster优先级约束(即以zone的访问顺序)为例说明。
其中用到的重要概念
强连通分量(strongly connected components): 有向图G中,任意两个顶点都强连通(stronglyconnected),即互相有可达的有向路径。则称G为强连通分量。
分量路径(component path): 以分量(本文指的是强连通分量)为单位组成的路径
将历史数据中的一条route的sequence通过如下步骤分成分量路径 4
step1:由历史的stop sequence构建有向图
step2:通过深度优先搜索将有向图变成 palm tree 结构
step3:从palm tree得到强连通分量 以及 分量路径
对于step1很简单,不再此赘述。
对于step2 通过深度优先搜索将有向图变成 palm tree 结构
可以先拿一个简单的无向图例子
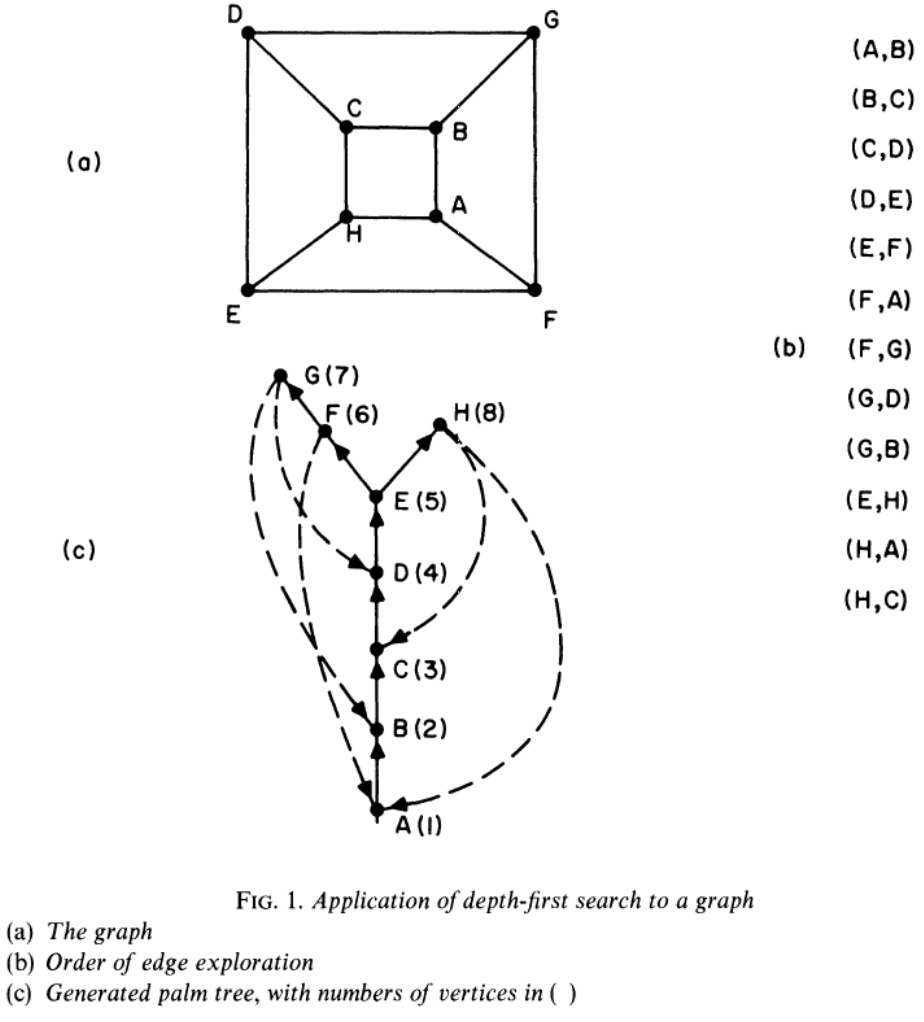
首先,会按字母顺序从A开始访问,然后查找A能抵达且未访问过的节点{B, H, F},然后按字母顺序访问B,然后查找B能抵达且未访问过的节点{C, G},则按字母顺序访问C,然后查找C能抵达且未访问过的节点{D, H},然后按字母顺序访问D,然后查找D能抵达且未访问过的节点{E, G},则按字母顺序访问E,然后查找E能抵达且未访问过的节点{F,H},然后按字母顺序访问F,然后查找F能抵达且未访问过的节点{G},然后按字母顺序访问G,此时发现G 不存在能抵达且未访问过的节点,则回头找G的上一个点即F,发现F也不存在能抵达且未访问过的节点,则再回头找F的上一个点即E,然后发现此时能抵达且未访问过的节点{H},则访问H,此时已经访问完所有,停止搜索。
然后就得到了图中(c)的实线部分,再把(a)中剩下的路径以虚线画到(c),就得到了 palm tree 结构
注意到palm tree 结构中实线部分是原始有向图中的节点间访问时的“主干”路径;而虚线则能够“走回头路”,即构成环的部分
则对于有向图而言,同理可得到(b) palm tree结构
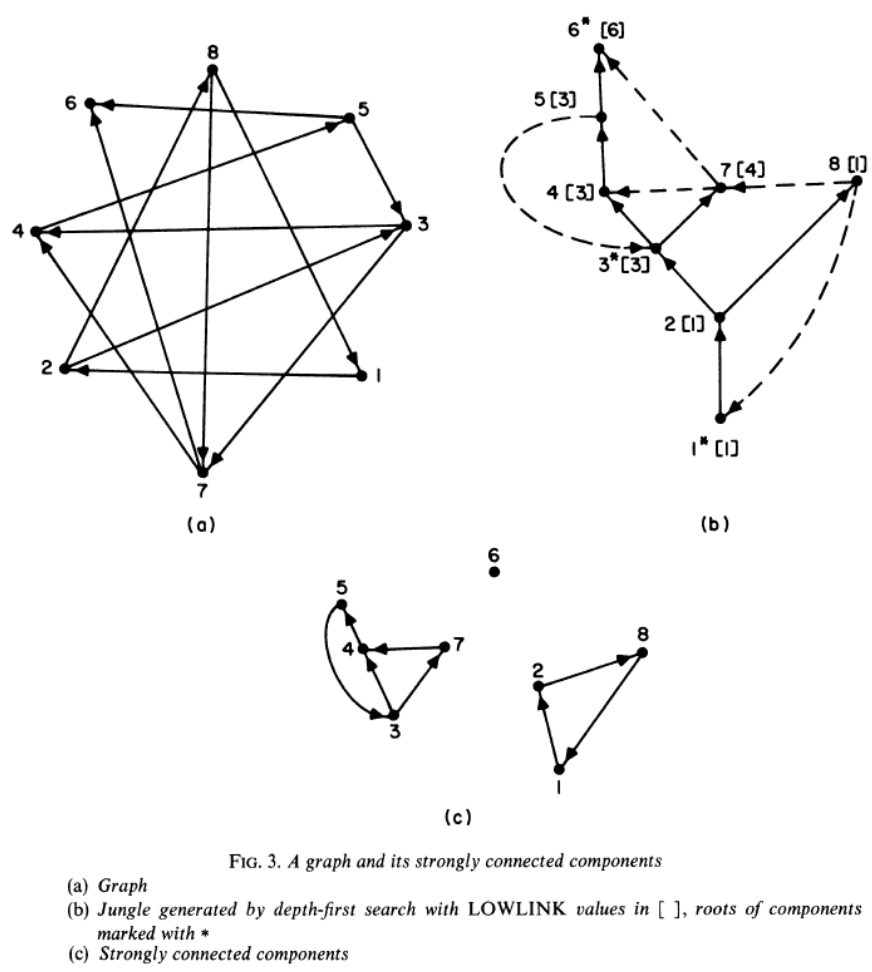
再然后再遍历每条虚线,如果虚线的重点到起点是可以通过实线可达的,则所经过的节点和边构成一个强连通子图。
比如对于虚线边(5, 3),发现3到5可以通过实线边3->4->5,可达。则点{3,4,5}和边{(3,4),(4,5),(5,3)}组成的图是一个强连通子图。
再将考虑指向这个强连通子图的线,比如实线(2,3),则需要从{3,4,5}中找一个虚线路径抵达2,发现没有,则不纳入;再比如虚线(7, 4),则要从{3,4,5}中找一个实线路径抵达7,发现(3,7)可以,则7和对应的边也纳入强连通子图。
其实就是缩小了寻找的范围,考虑虚线时,则需要找一个实线路径可达;考虑实线时,则需要找一个虚线路径可达
以此反复即可找到各个尽可能大的强连通分量即图(c)。
对于step3 从palm tree得到强连通分量 以及 分量路径
这时有趣的地方来了,强连通分量的路径是单向的,在图c中强连通分量的路径是红色箭头所示,这表明{1,2,8}必须要在{3,4,5,7}前访问,也就是说优先级由高到低是{1,2,8} > {3,4,5,7} > {6}
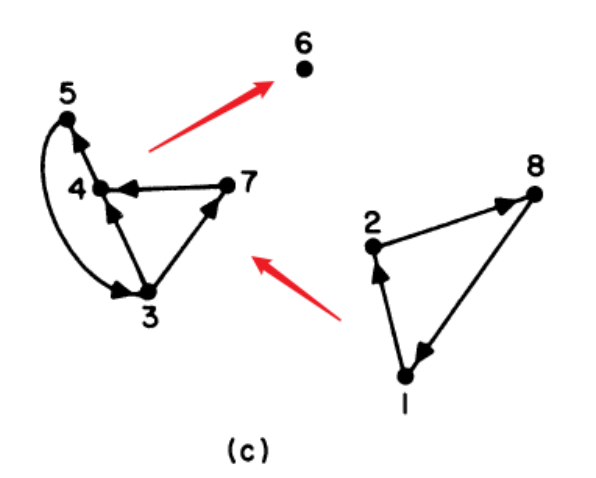
这时可能好奇,那历史中有这么多条sequence,得到的优先级有冲突怎么?
· 对于历史数据中的1条sequence,发现优先级a>b时,则precedence(a,b) =precedence(a,b) +1 *weight;若优先级a
· weight是根据route的sequence的质量high, medium, low依次为2, 1.5, 1
· 更进一步,precedence(a,b) 优先级大小也是可以利用的。
(4)用改进后的LKH-3求解
作者主要用到
Concorde求解器(用来查看最优时的结果)和
LKH-3求解算法(最终提交时采用的求次优解的方法,因为比赛有运行时间限制)。
TSP领域公认比较出名的求解器/求解算法:
(1)求精确最优解——Concorde
Concorde原始版本是用ANSIC编程语言编写的。Concorde的TSP求解器已用于获得所有110个
TSPLIB实例的最优解;最大的城市有85900个。
Concorde官网
(https://www.math.uwaterloo.ca/tsp/concorde.html)
Concorde的python易用版本
(https://github.com/jingw2/pyconcorde)
(2)启发式求近似最优解——LKH
最新的LKH-3
(http://webhotel4.ruc.dk/~keld/research/LKH-3/)
不仅可以快速求解:
TSP: Symmetric traveling salesman problem
ATSP: Asymmetric traveling salesman problem
HCP: Hamiltonian cycle problem
HPP: Hamiltonian path problem
还可以求解:
ACVRP: Asymmetric capacitated vehicle routing problem
ADCVRP: Asymmetric distance constrained vehicle routing problem
BWTSP: Black and white traveling salesman problem
CCVRP: Cumulative capacitated vehicle routing problem
CTSP: Colored traveling salesman problem
CVRP: Capacitated vehicle routing problem
CVRPTW: Capacitated vehicle routing problem with time windows
DCVRP: Distance constrained capacitated vehicle routing problem
1-PDTSP: One-commodity pickup-and-delivery traveling salesman problem
m-PDTSP: Multi-commodity pickup-and-delivery traveling salesman problem
m1-PDTSP: Multi-commodity one-to-one pickup-and-delivery traveling salesman problem
MLP: Minimum latency problem
MTRP: Multiple traveling repairman problem
MTRPD: Multiple traveling repairman problem with distance constraints
mTSP: Multiple traveling salesmen problem
OCMTSP: Open close multiple traveling salesman problem
OVRP: Open vehicle routing problem
PDPTW: Pickup-and-delivery problem with time windows
PDTSP: Pickup-and-delivery traveling salesman problem
PDTSPF: Pickup-and-delivery traveling salesman problem with FIFO loading
PDTSPL: Pickup-and-delivery traveling salesman problem with LIFO loading
RCTVRP: Risk-constrained cash-in-transit vehicle routing problem
RCTVRPTW: Risk-constrained cash-in-transit vehicle routing with time windows
SOP: Sequential ordering problem
STTSP: Steiner traveling salesman problem
TRP: Traveling repairman problem
TSPDL: Traveling salesman problem with draft limits
TSPPD: Traveling salesman problem with pickups and deliveries
TSPTW: Traveling salesman problem with time windows
VRPB: Vehicle routing problem with backhauls
VRPBTW: Vehicle routing problem with backhauls and time windows
VRPMPD: Vehicle routing problem with mixed pickup and delivery
VRPMPDTW: Vehicle routing problem with mixed pickup and delivery and time windows
VRPSPD: Vehicle routing problem with simultaneous pickup and delivery
VRPSPDTW: Vehicle routing problem with simultaneous pickup-delivery and time windows
想知道其他求解TSP方法也可以看看我们的往期文章
https://mp.weixin.qq.com/s/eAb5bLoTQxwD6EuPavuRjQ
结果
作者原文比较散乱
没有整理结果
小编在此整理了下作者实验的结果

LKH-AMZ是作者对LKH-3进行了一些约束条件方面的扩展
题外话环节
作者原文中还是很多其他细节的
比如训练集和测试集的划分、ATSP的3-opt和4-opt、路径合并、敏感性分析等等
朋友们是进一步了解这些细节呢
还是想看一下第2、3名的解决方案呢
(挖坑)

参考资料
1. Cook, W., Held, S., & Helsgaun, K. (2021). Local Search with Learned Constraints for Last Mile Routing. In Winkenbach, M., Parks, S., &Noszek, J. (Eds.), Technical Proceedings of the 2021 Amazon Last Mile Routing Research Challenge (pp. XXI.1–XXI.12). MIT Libraries. https://hdl.handle.net/1721.1/131235
2. Xiaotong Guo, Baichuan Mo and Qingyi Wang. (2021). Last-Mile Delivery Trajectory Prediction Using Hierarchical TSP with Customized Cost Matrix. In Winkenbach, M., Parks, S., & Noszek, J. (Eds.), Technical Proceedings of the 2021 Amazon Last Mile Routing Research Challenge (pp. II.1–II.12). MIT Libraries. https://hdl.handle.net/1721.1/131235
3. Okan Arslan and Rasit Abay. (2021). Data-Driven Vehicle Routing in Last-Mile Delivery. In Winkenbach, M., Parks, S., & Noszek, J.(Eds.),echnical Proceedings of the 2021 Amazon Last Mile Routing Research Challenge (pp. VI.1–VI.14). MIT Libraries. https://hdl.handle.net/1721.1/131235
4. Tarjan, R. (1972). Depth-first search and linear graph algorithms. SIAM Journal on Computing, 1 , 146-160.doi:10.1137/0201010.
5. Helsgaun, K. (2017). An extension of the Lin-Kernighan-Helsgaun TSP solver for constrained traveling salesman and vehicle routing problems. Technical Report Roskilde Universitet. URL: http://akira.ruc.dk/~keld/research/LKH/LKH-3_REPORT.pdf.
- END -
文案:丘润文、王月婷(华南理工大学工商管理学院研究生一年级)、谢旖(华南理工大学工商管理学院研究生二年级)
指导老师:朱文斌(华南理工大学工商管理学院)
排版:程欣悦(荆楚理工学院本科四年级)
如对文中内容有疑问,欢迎交流。PS:部分资料来自网络。
如有需求,可以联系:朱文斌(华南理工大学工商管理学院:i@zhuwb.com)丘润文(华南理工大学工商管理学院研究生一年级:bmqiurunwen@mail.scut.edu.cn)程欣悦(荆楚理工学院本科四年级:1293900389@qq.com)
【END】
