超详细图解Self-Attention的那些事儿
点击上方“程序员大白”,选择“星标”公众号
重磅干货,第一时间送达

Self-Attention 是 Transformer最核心的思想,最近几日重读论文,有了一些新的感想。由此写下本文与读者共勉。
笔者刚开始接触Self-Attention时,最大的不理解的地方就是Q K V三个矩阵以及我们常提起的Query查询向量等等,现在究其原因,应当是被高维繁复的矩阵运算难住了,没有真正理解矩阵运算的核心意义。因此,在本文开始之前,笔者首先总结一些基础知识,文中会重新提及这些知识蕴含的思想是怎样体现在模型中的。
一些基础知识
向量的内积是什么,如何计算,最重要的,其几何意义是什么? 一个矩阵 与其自身的转置相乘,得到的结果有什么意义?
1. 键值对注意力
这一节我们首先分析Transformer中最核心的部分,我们从公式开始,将每一步都绘制成图,方便读者理解。
键值对Attention最核心的公式如下图。其实这一个公式中蕴含了很多个点,我们一个一个来讲。请读者跟随我的思路,从最核心的部分入手,细枝末节的部分会豁然开朗。
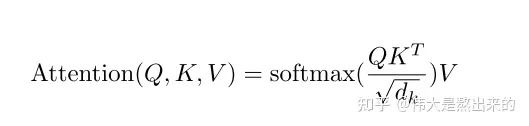
假如上面的公式很难理解,那么下面的公式读者能否知道其意义是什么呢?
我们先抛开Q K V三个矩阵不谈,self-Attention最原始的形态其实长上面这样。那么这个公式到底是什么意思呢?
我们一步一步讲
代表什么?
一个矩阵乘以它自己的转置,会得到什么结果,有什么意义?
我们知道,矩阵可以看作由一些向量组成,一个矩阵乘以它自己转置的运算,其实可以看成这些向量分别与其他向量计算内积。(此时脑海里想起矩阵乘法的口诀,第一行乘以第一列、第一行乘以第二列......嗯哼,矩阵转置以后第一行不就是第一列吗?这是在计算第一个行向量与自己的内积,第一行乘以第二列是计算第一个行向量与第二个行向量的内积第一行乘以第三列是计算第一个行向量与第三个行向量的内积.....)
回想我们文章开头提出的问题,向量的内积,其几何意义是什么?
答:表征两个向量的夹角,表征一个向量在另一个向量上的投影
记住这个知识点,我们进入一个超级详细的实例:
我们假设 ,其中 为一个二维矩阵, 为一个行向量(其实很多教材都默认向量是列向量,为了方便举例请读者理解笔者使用行向量)。对应下面的图, 对应"早"字embedding之后的结果,以此类推。
下面的运算模拟了一个过程,即 。我们来看看其结果究竟有什么意义
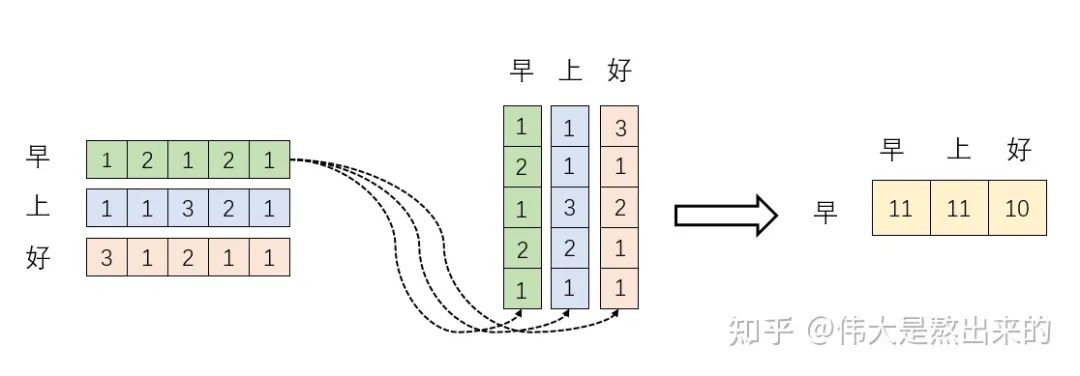
首先,行向量 分别与自己和其他两个行向量做内积("早"分别与"上""好"计算内积),得到了一个新的向量。我们回想前文提到的向量的内积表征两个向量的夹角,表征一个向量在另一个向量上的投影。那么新的向量向量有什么意义的?是行向量 在自己和其他两个行向量上的投影。我们思考,投影的值大有什么意思?投影的值小又如何?
投影的值大,说明两个向量相关度高。
我们考虑,如果两个向量夹角是九十度,那么这两个向量线性无关,完全没有相关性!
更进一步,这个向量是词向量,是词在高维空间的数值映射。词向量之间相关度高表示什么?是不是在一定程度上(不是完全)表示,在关注词A的时候,应当给予词B更多的关注?
上图展示了一个行向量运算的结果,那么矩阵 的意义是什么呢?
矩阵 是一个方阵,我们以行向量的角度理解,里面保存了每个向量与自己和其他向量进行内积运算的结果。
至此,我们理解了公式 中, 的意义。我们进一步,Softmax的意义何在呢?请看下图
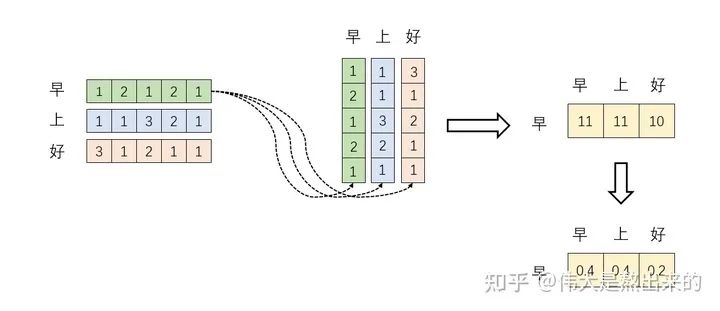
我们回想Softmax的公式,Softmax操作的意义是什么呢?
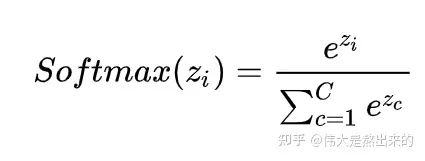
答:归一化
我们结合上面图理解,Softmax之后,这些数字的和为1了。我们再想,Attention机制的核心是什么?
加权求和
那么权重从何而来呢?就是这些归一化之后的数字。当我们关注"早"这个字的时候,我们应当分配0.4的注意力给它本身,剩下0.4关注"上",0.2关注"好"。当然具体到我们的Transformer,就是对应向量的运算了,这是后话。
行文至此,我们对这个东西是不是有点熟悉?Python中的热力图Heatmap,其中的矩阵是不是也保存了相似度的结果?
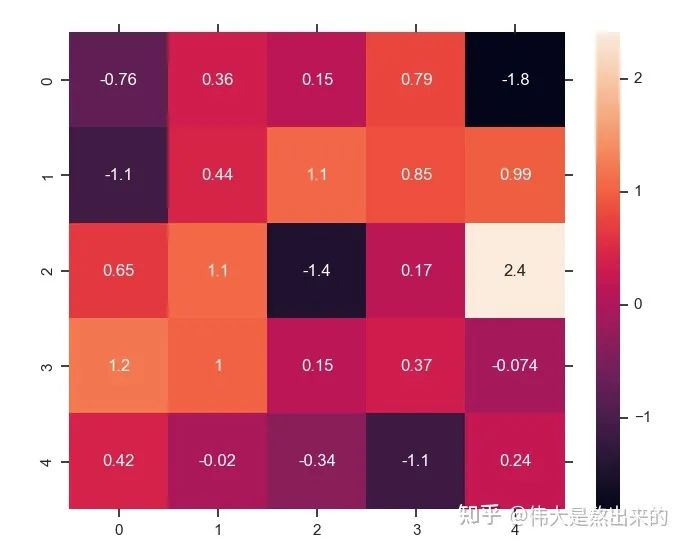
我们仿佛已经拨开了一些迷雾,公式 已经理解了其中的一半。最后一个 X 有什么意义?完整的公式究竟表示什么?我们继续之前的计算,请看下图
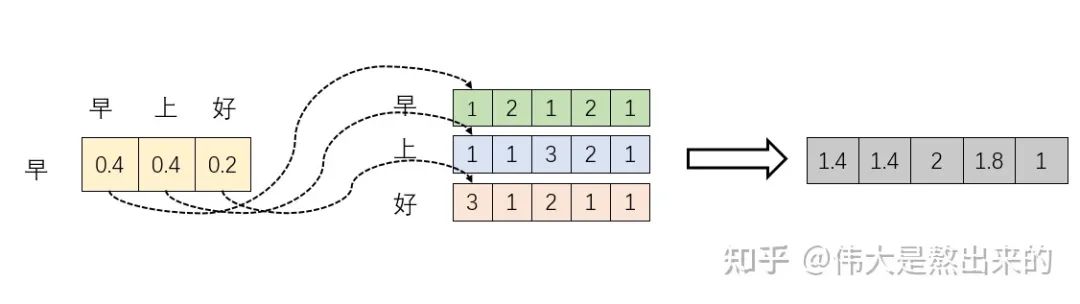
我们取 的一个行向量举例。这一行向量与 的一个列向量相乘,表示什么?
观察上图,行向量与 的第一个列向量相乘,得到了一个新的行向量,且这个行向量与 的维度相同。
在新的向量中,每一个维度的数值都是由三个词向量在这一维度的数值加权求和得来的,这个新的行向量就是"早"字词向量经过注意力机制加权求和之后的表示。
一张更形象的图是这样的,图中右半部分的颜色深浅,其实就是我们上图中黄色向量中数值的大小,意义就是单词之间的相关度(回想之前的内容,相关度其本质是由向量的内积度量的)!
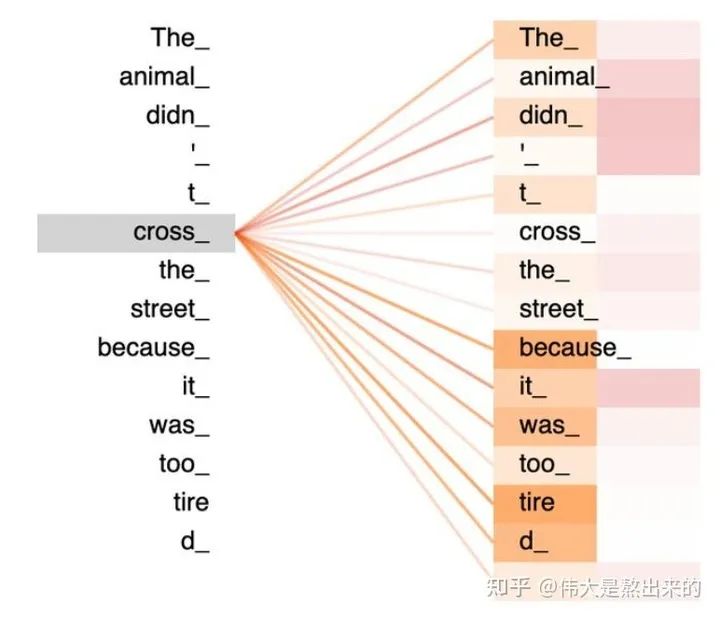
如果您坚持阅读到这里,相信对公式 已经有了更深刻的理解。
我们接下来解释原始公式中一些细枝末节的问题
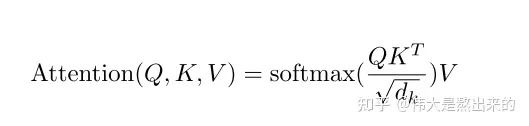
2. Q K V矩阵
在我们之前的例子中并没有出现Q K V的字眼,因为其并不是公式中最本质的内容。
Q K V究竟是什么?我们看下面的图
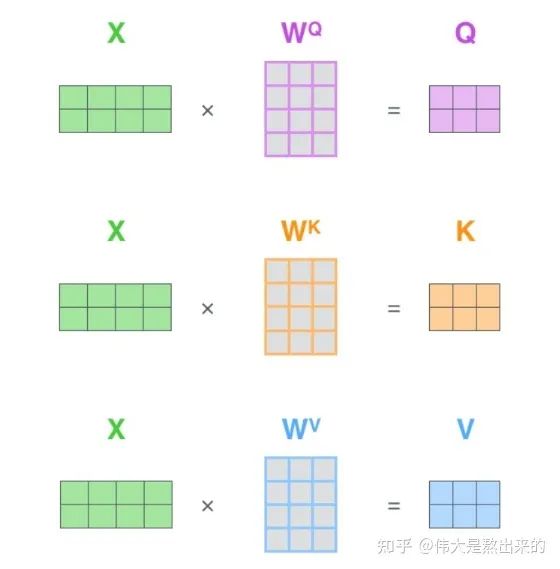
其实,许多文章中所谓的Q K V矩阵、查询向量之类的字眼,其来源是 与矩阵的乘积,本质上都是 的线性变换。
为什么不直接使用 而要对其进行线性变换?
当然是为了提升模型的拟合能力,矩阵 都是可以训练的,起到一个缓冲的效果。
如果你真正读懂了前文的内容,读懂了 这个矩阵的意义,相信你也理解了所谓查询向量一类字眼的含义。
3. 的意义
假设 里的元素的均值为0,方差为1,那么 中元素的均值为0,方差为d. 当d变得很大时, 中的元素的方差也会变得很大,如果 中的元素方差很大,那么 的分布会趋于陡峭(分布的方差大,分布集中在绝对值大的区域)。总结一下就是 的分布会和d有关。因此 中每一个元素除以 后,方差又变为1。这使得 的分布“陡峭”程度与d解耦,从而使得训练过程中梯度值保持稳定。
至此Self-Attention中最核心的内容已经讲解完毕,关于Transformer的更多细节可以参考我的这篇回答:
最后再补充一点,对self-attention来说,它跟每一个input vector都做attention,所以没有考虑到input sequence的顺序。更通俗来讲,大家可以发现我们前文的计算每一个词向量都与其他词向量计算内积,得到的结果丢失了我们原来文本的顺序信息。对比来说,LSTM是对于文本顺序信息的解释是输出词向量的先后顺序,而我们上文的计算对sequence的顺序这一部分则完全没有提及,你打乱词向量的顺序,得到的结果仍然是相同的。
这就牵扯到Transformer的位置编码了,我们按住不表。
Self-Attention的代码实现
# Muti-head Attention 机制的实现
from math import sqrt
import torch
import torch.nn
class Self_Attention(nn.Module):
# input : batch_size * seq_len * input_dim
# q : batch_size * input_dim * dim_k
# k : batch_size * input_dim * dim_k
# v : batch_size * input_dim * dim_v
def __init__(self,input_dim,dim_k,dim_v):
super(Self_Attention,self).__init__()
self.q = nn.Linear(input_dim,dim_k)
self.k = nn.Linear(input_dim,dim_k)
self.v = nn.Linear(input_dim,dim_v)
self._norm_fact = 1 / sqrt(dim_k)
def forward(self,x):
Q = self.q(x) # Q: batch_size * seq_len * dim_k
K = self.k(x) # K: batch_size * seq_len * dim_k
V = self.v(x) # V: batch_size * seq_len * dim_v
atten = nn.Softmax(dim=-1)(torch.bmm(Q,K.permute(0,2,1))) * self._norm_fact # Q * K.T() # batch_size * seq_len * seq_len
output = torch.bmm(atten,V) # Q * K.T() * V # batch_size * seq_len * dim_v
return output

# Muti-head Attention 机制的实现
from math import sqrt
import torch
import torch.nn
class Self_Attention_Muti_Head(nn.Module):
# input : batch_size * seq_len * input_dim
# q : batch_size * input_dim * dim_k
# k : batch_size * input_dim * dim_k
# v : batch_size * input_dim * dim_v
def __init__(self,input_dim,dim_k,dim_v,nums_head):
super(Self_Attention_Muti_Head,self).__init__()
assert dim_k % nums_head == 0
assert dim_v % nums_head == 0
self.q = nn.Linear(input_dim,dim_k)
self.k = nn.Linear(input_dim,dim_k)
self.v = nn.Linear(input_dim,dim_v)
self.nums_head = nums_head
self.dim_k = dim_k
self.dim_v = dim_v
self._norm_fact = 1 / sqrt(dim_k)
def forward(self,x):
Q = self.q(x).reshape(-1,x.shape[0],x.shape[1],self.dim_k // self.nums_head)
K = self.k(x).reshape(-1,x.shape[0],x.shape[1],self.dim_k // self.nums_head)
V = self.v(x).reshape(-1,x.shape[0],x.shape[1],self.dim_v // self.nums_head)
print(x.shape)
print(Q.size())
atten = nn.Softmax(dim=-1)(torch.matmul(Q,K.permute(0,1,3,2))) # Q * K.T() # batch_size * seq_len * seq_len
output = torch.matmul(atten,V).reshape(x.shape[0],x.shape[1],-1) # Q * K.T() * V # batch_size * seq_len * dim_v
return output推荐阅读
关于程序员大白
程序员大白是一群哈工大,东北大学,西湖大学和上海交通大学的硕士博士运营维护的号,大家乐于分享高质量文章,喜欢总结知识,欢迎关注[程序员大白],大家一起学习进步!

