剪视频剪出一个贪心算法……

对于非专业剪辑玩家,不做什么宏大特效电影镜头,只是做个视频教程,其实也没啥难度,只需要把视频剪流畅,所以用到最多的功能就是切割功能,然后删除和拼接视频片接。
没有剪过视频的读者可能不知道,在常用的剪辑软件中视频被切割成若干片段之后,每个片段都可以还原成原始视频。
就比如一个 10 秒的视频,在中间切一刀剪成两个 5 秒的视频,这两个五秒的视频各自都可以还原成 10 秒的原视频。就好像蚯蚓,把自己切成 4 段就能搓麻,把自己切成 11 段就可以凑一个足球队。
剪视频时,每个视频片段都可以抽象成了一个个区间,时间就是区间的端点,这些区间有的相交,有的不相交……
假设剪辑软件不支持将视频片段还原成原视频,那么如果给我若干视频片段,我怎么将它们还原成原视频呢?
这是个很有意思的区间算法问题,也是力扣第 1024 题「视频拼接」,题目如下:

函数签名如下:
int videoStitching(int[][] clips, int T);
记得以前写过好几篇区间相关的问题:
区间问题合集 写过求区间交集、区间并集、区间覆盖这几个问题。
贪心算法做时间管理 写过利用贪心算法求不相交的区间。
算上本文的区间剪辑问题,经典的区间问题也就都讲完了。
思路分析
题目并不难理解,给定一个目标区间和若干小区间,如何通过裁剪和组合小区间拼凑出目标区间?最少需要几个小区间?
前文多次说过,区间问题肯定按照区间的起点或者终点进行排序。
因为排序之后更容易找到相邻区间之间的联系,如果是求最值的问题,可以使用贪心算法进行求解。
区间问题特别容易用贪心算法,公众号历史文章除了 贪心算法之区间调度,还有一篇 贪心算法玩跳跃游戏,其实这个跳跃游戏就相当于一个将起点排序的区间问题,你细品,你细品。
至于到底如何排序,这个就要因题而异了,我做这道题的思路是先按照起点升序排序,如果起点相同的话按照终点降序排序。
为什么这样排序呢,主要考虑到这道题的以下两个特点:
1、要用若干短视频凑出完成视频[0, T],至少得有一个短视频的起点是 0。
这个很好理解,如果没有一个短视频是从 0 开始的,那么区间[0, T]肯定是凑不出来的。
2、如果有几个短视频的起点都相同,那么一定应该选择那个最长(终点最大)的视频。
这一条就是贪心的策略,因为题目让我们计算最少需要的短视频个数,如果起点相同,那肯定是越长越好,不要白不要,多出来了大不了剪辑掉嘛。
基于以上两个特点,将clips按照起点升序排序,起点相同的按照终点降序排序,最后得到的区间顺序就像这样:
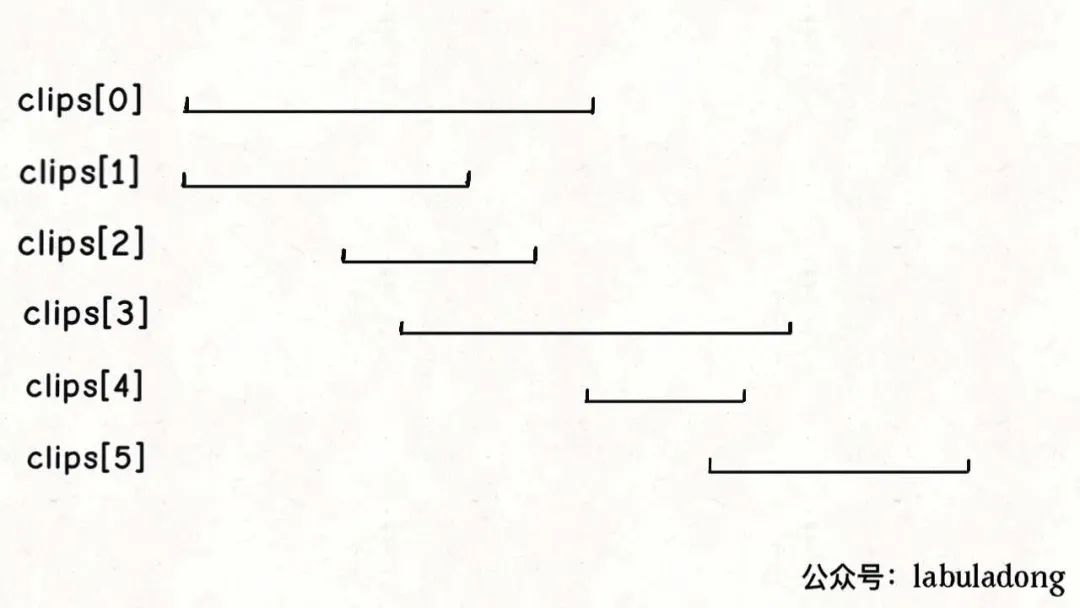
这样我们就可以确定,如果clips[0]是的起点是 0,那么clips[0]这个视频一定会被选择。
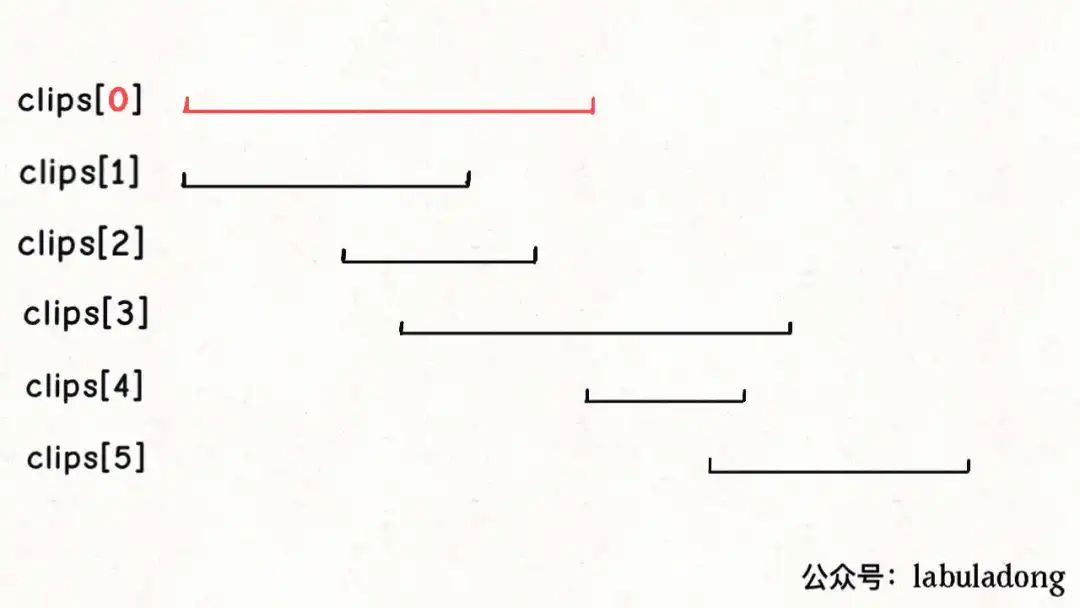
当我们确定clips[0]一定会被选择之后,就可以选出第二个会被选择的视频:
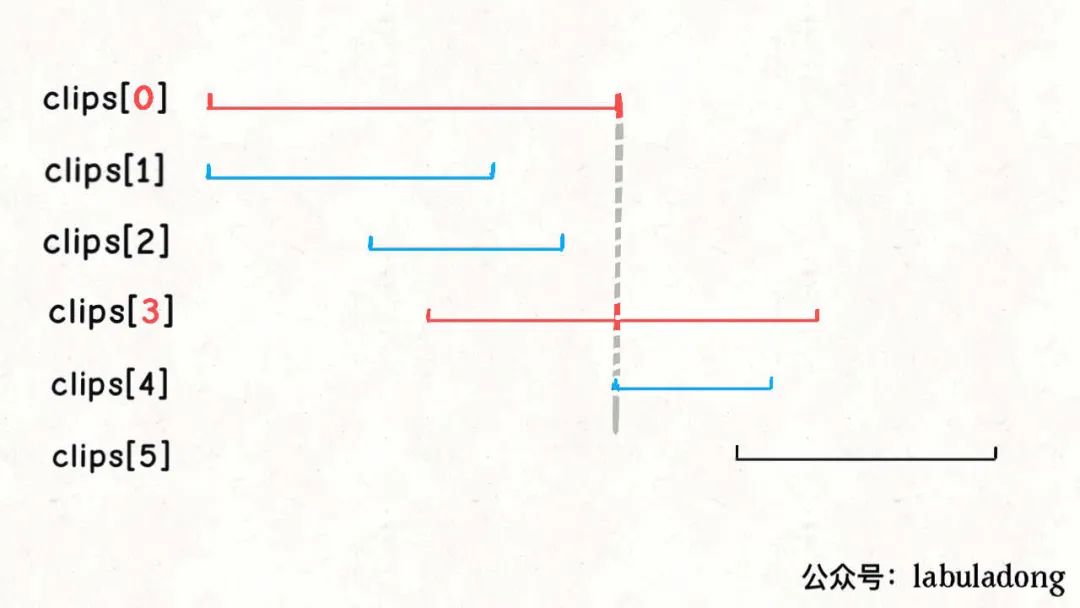
我们会比较所有起点小于clips[0][1]的区间,根据贪心策略,它们中终点最大的那个区间就是第二个会被选中的视频。
然后可以通过第二个视频区间贪心选择出第三个视频,以此类推,直到覆盖区间[0, T],或者无法覆盖返回 -1。
以上就是这道题的解题思路,仔细想想,这题的核心和前文 贪心算法玩跳跃游戏 写的跳跃游戏是相同的,如果你能看出这两者的联系,就可以说理解贪心算法的奥义了。
代码实现
实现上述思路需要我们用两个变量curEnd和nextEnd来进行:
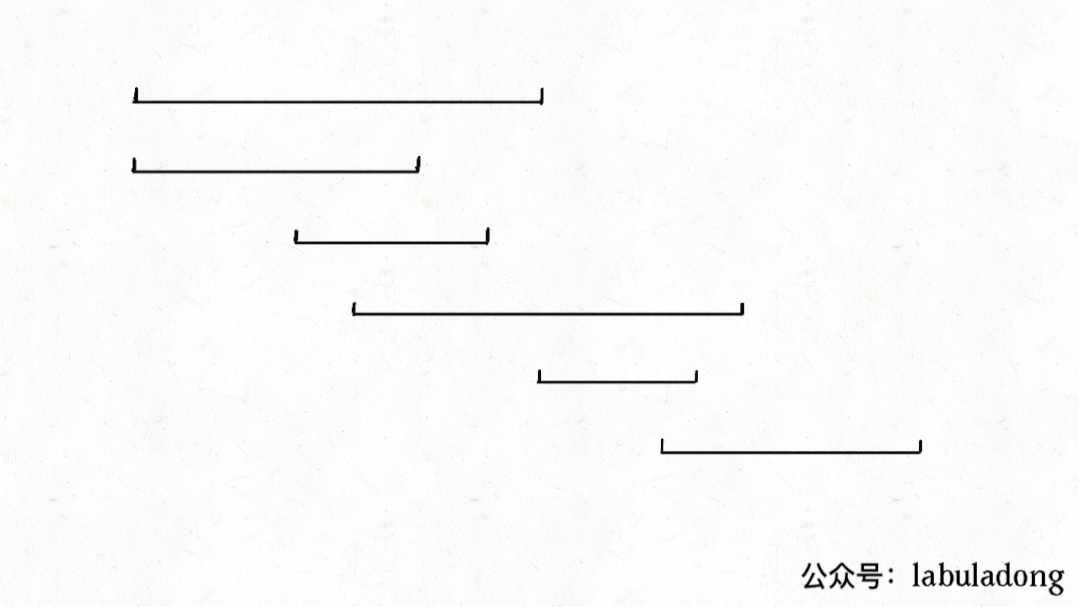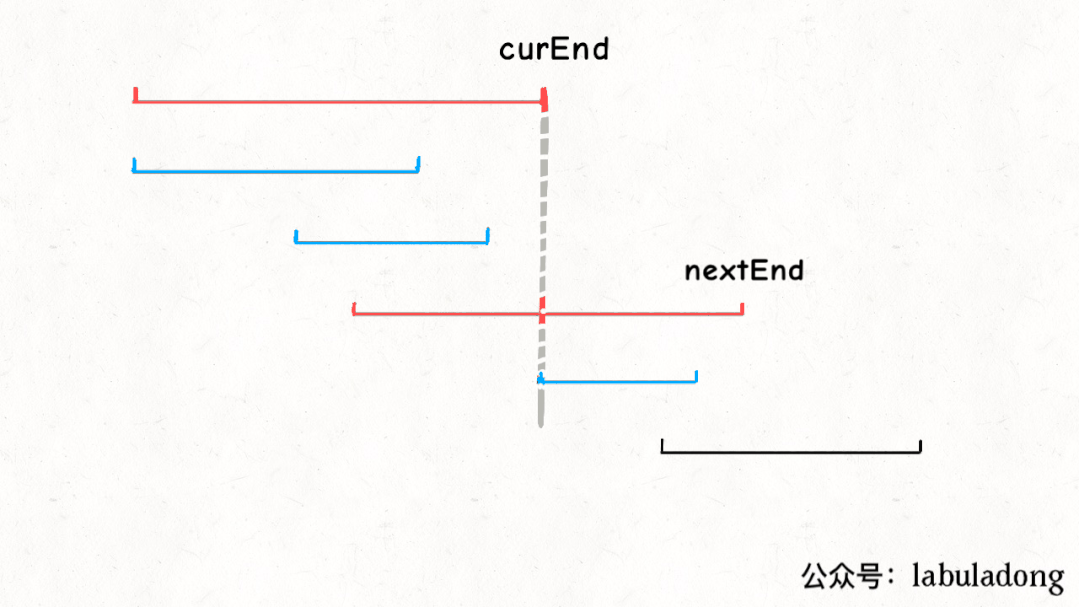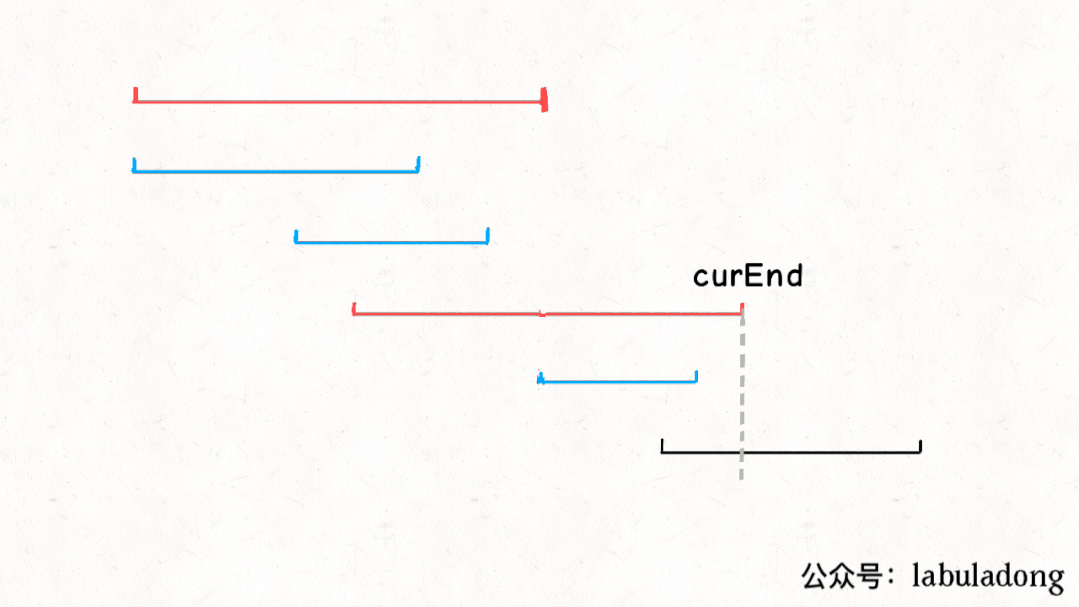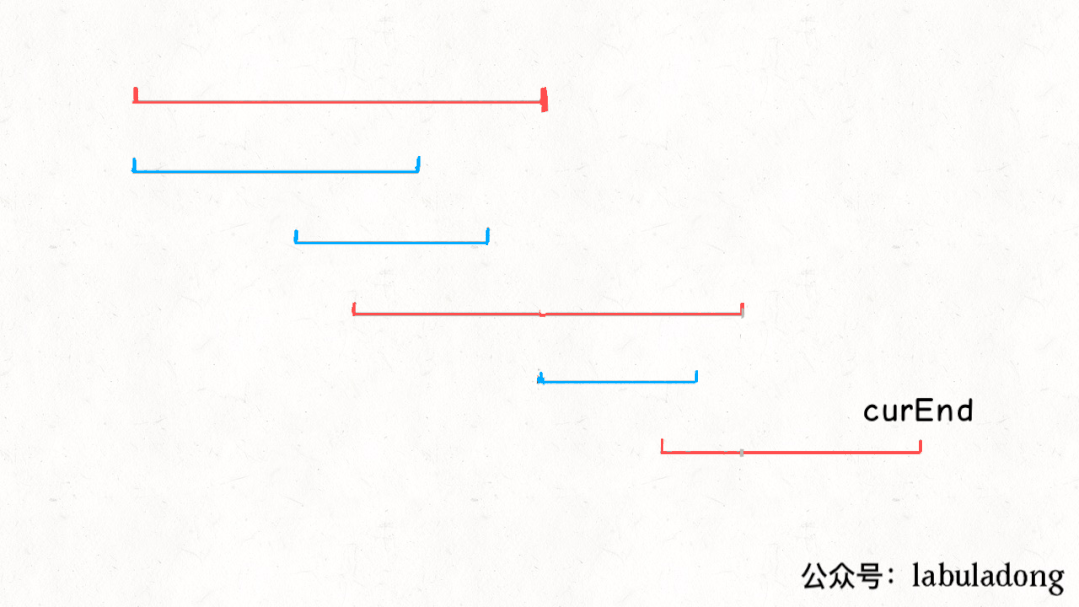
最终代码实现如下:
int videoStitching(int[][] clips, int T) {
if (T == 0) return 0;
// 按起点升序排列,起点相同的降序排列
Arrays.sort(clips, (a, b) -> {
if (a[0] == b[0]) {
return b[1] - a[1];
}
return a[0] - b[0];
});
// 记录选择的短视频个数
int res = 0;
int curEnd = 0, nextEnd = 0;
int i = 0, n = clips.length;
while (i < n && clips[i][0] <= curEnd) {
// 在第 res 个视频的区间内贪心选择下一个视频
while (i < n && clips[i][0] <= curEnd) {
nextEnd = Math.max(nextEnd, clips[i][1]);
i++;
}
// 找到下一个视频,更新 curEnd
res++;
curEnd = nextEnd;
if (curEnd >= T) {
// 已经可以拼出区间 [0, T]
return res;
}
}
// 无法连续拼出区间 [0, T]
return -1;
}
这段代码的时间复杂度是多少呢?虽然代码中有一个嵌套的 while 循环,但这个嵌套 while 循环的时间复杂度是O(N)。因为当i递增到n时循环就会结束,所以这段代码只会执行O(N)次。
但是别忘了我们对clips数组进行了一次排序,消耗了O(NlogN)的时间,所以本算法的总时间复杂度是O(NlogN)。


▊《labuladong的算法小抄》
付东来(@labuladong) 著
用喜闻乐见的语言讲算法
GitHub 68.8K star的硬核算法教程
(京东限时活动,快快扫码抢购吧!)

如果喜欢本文 欢迎 在看丨留言丨分享至朋友圈 三连 热文推荐
▼点击阅读原文,查看本书详情~
