LeetCode 啥题都有:Go 刷「打家劫舍」二
上次刷了一道动态规划的题目:Leetcode-198. 打家劫舍I ,今天我们来看它的进阶版II。
介绍

这是 House Robber II,也就是 I 的变型版本。II 和 I 的最大区别在于 II 把房子围成一个圈了。这意味着第一幢房子和最后一幢房子是紧挨着的。根据规则,两间相邻的房子不能同时偷,对小偷打击还是蛮大的。
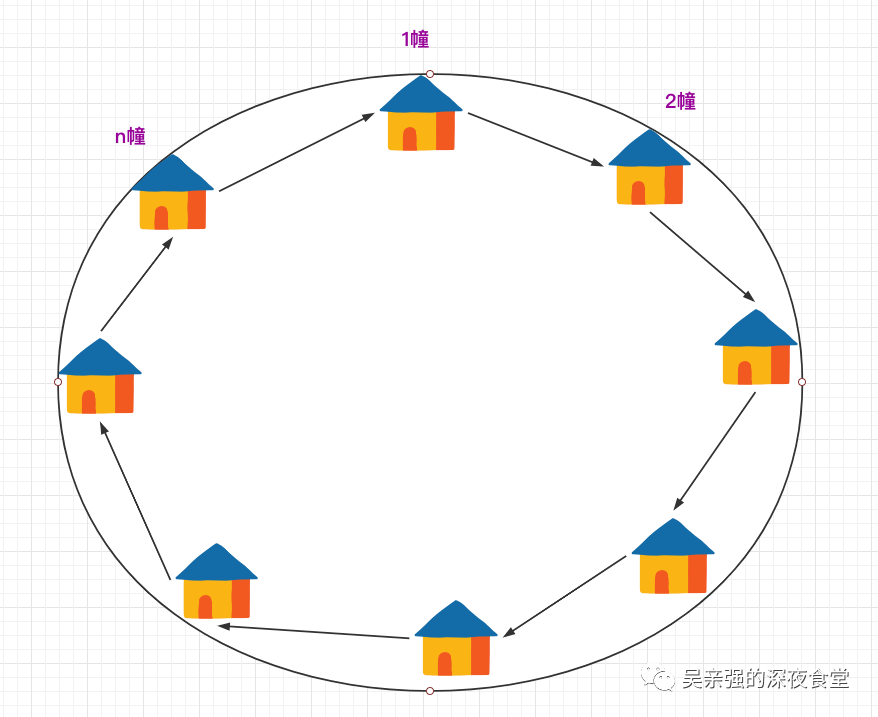
小偷在不触发报警装置的情况下,针对这类场景,如何让自己偷窃的利益最大化?
解题
上面提到,相邻两家不能同时偷。但是如果只有一家,那么构不成相邻的条件,就偷唯一的那户人家。
如果有两家,那么偷的必然是两家中钱多的那家。
那如果总数大于 2 家呢?
对于第 n 家来说,只有两种选择:偷或者不偷。
是咋么计算出当前这家是否要偷的呢。
我们假设当前这家编号为 n,那么,
max(偷第 n 家的钱 + dp[截止第 n-2 家偷的钱], dp[截止第 n-1 家偷的钱])。这才是这道关于动态规划最核心的一个点。
看懂了吗?没看懂也没关系,手把手摸个图片出来。 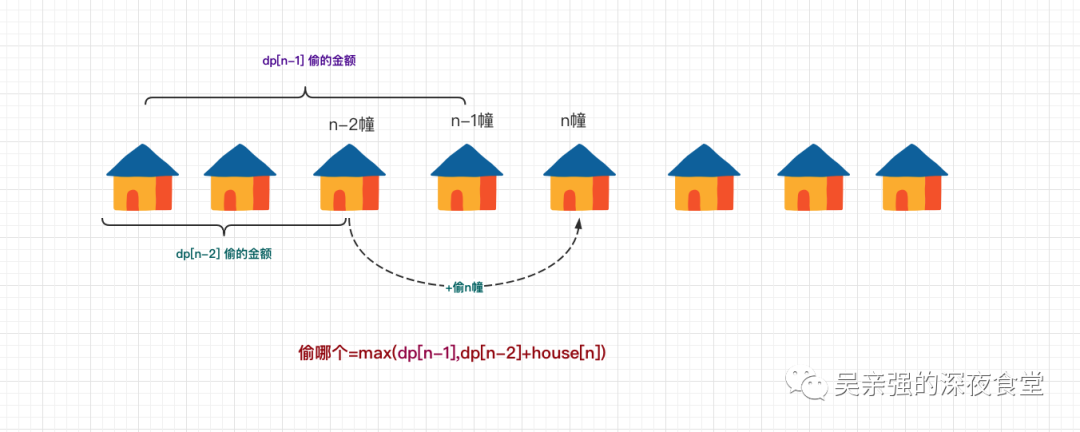
还没看懂,加我微信 remember_wuqinqiang 我告诉你。这里顺便打个广告,没加我好友的赶紧加我好友。
最后,还需要考虑一个问题,如何确保偷了第一家就不偷最后一家,偷最后一家就不偷第一家的情况。 很简单,直接定义两个 dp,一个范围不包括第一家,一个范围不包括最后一家。 最后我们变成了求:
// 伪代码
最佳偷钱:=max(dp[不包括第一家],dp[不包括最后一家])那么剩下的就是对两个 dp 的状态转移公式了。
func rob(nums []int) int {
n := len(nums)
if n == 0 {
return 0
}
if n == 1 {
return nums[0]
}
dp1, dp2 := make([]int, n), make([]int, n)
dp1[0] = nums[0]
dp1[1] = max(dp1[0], nums[1])
dp2[0] = 0 //dp2 不偷第一家
dp2[1] = max(dp2[0], nums[1])
for i := 2; i < n; i++ {
if i < n-1 { // dp1 不偷最后一家
dp1[i] = max(dp1[i-1], dp1[i-2]+nums[i])
} else {
dp1[i] = dp1[i-1]
}
dp2[i] = max(dp2[i-1], dp2[i-2]+nums[i])
}
return max(dp2[n-1], dp1[n-1])
}
func max(x int, y int) int {
if x > y {
return x
}
return y
}其实代码还能更简洁。
func rob(nums []int) int {
n := len(nums)
if n == 0 {
return 0
}
if n == 1 {
return nums[0]
}
if n == 2 {
return max(nums[0], nums[1])
}
return max(helper(nums[1:]), helper(nums[:n-1]))
}
func helper(nums []int) int {
first, second := nums[0], max(nums[0], nums[1])
for _, v := range nums[2:] {
first, second = second, max(second, first+v)
}
return second
}
func max(a, b int) int {
if a > b {
return a
}
return b
}今天的题就分享到这了。
推荐阅读
评论
