蒙特卡罗方法如何化简为繁
本文不用公式,仅仅是想说明这种方法的基本思想以及潜在应用。由于该方法应用广泛,技术细节值得深入研究,因此需要一系列文章来阐述,本号后面会陆续展开。
1
引 言
蒙特卡罗(Monte Carlo,MC)方法,是指使用随机性(貌似变繁了)来解决很多确定性问题(貌似是简单的)的方法。它们使用重复性随机采样的过程来进行未知参数的数值估计,是以概率统计理论为指导的数值计算方法。
MC 允许对涉及许多随机变量的复杂情况进行建模,其用途极为广泛,并在物理学、博弈论和金融领域带来了许多开创性的成果。2016 年,打败人类顶级围棋手的 AlphaGo 横空出世,背后的两大核心技术之一就是蒙特卡罗树搜索方法。
蒙特卡罗方法种类繁多,但是它们都有共同点,即它们依靠随机数生成来解决确定性问题。本篇概述 MC 的一些基本思想,并对它们潜在的应用有所了解。
想象一下在坐标网格上的一个
尽管这种关于随机采样的直观想法很简单,但它在实际应用中却广受亲睐,例如从法律到气候预测的许多领域都有广泛应用,并且与本文的主题(机器学习和统计)可能是最相关。它的正式名称正是: 蒙特卡罗方法。
当遇到一个由确定性原则组成的问题时,比如形状的面积、函数的分布、在游戏中玩家下一步应该选择什么操作等,蒙特卡罗方法可以假设可以通过概率和随机性来对这些问题建模。
蒙特卡罗方法依赖于来自某个分布的重复性随机采样来获得数值结果。这是一种方法,而不是一个具体的算法。
蒙特卡罗方法怎么来的?其实它并不是人名,而是摩纳哥的著名赌城。蒙特卡罗法作为一种计算方法,是由美国数学家乌拉姆(Stanislaw Ulam)与美籍匈牙利数学家冯·诺伊曼(John von Neumann)在 20 世纪 40 年代中叶,为研制核武器的需要而首先提出来的。乌拉姆在洛斯阿拉莫斯国家实验室从事核武器项目时,提出了马尔可夫链蒙特卡罗方法。乌拉姆取得突破后,约翰·冯·诺伊曼立刻意识到了它的重要性。冯·诺依曼在首台计算机 ENIAC 上编写程序以执行蒙特卡罗计算。
但实际上,该方法的基本思想早就被统计学家所采用了,例如早在 18 世纪,法国数学家蒲丰(或布丰)提出了用随机投针来计算圆周率的方法。下面,我们用这个类似思想但更简单的方法来计算
同时也作为一个基于形状的示例,请思考不使用任何数学方法(仅使用蒙特卡罗采样)来找出圆形面积的公式。随机采样可以用作找到函数积分(曲线下的面积)的简易方法。重要的是,圆周率
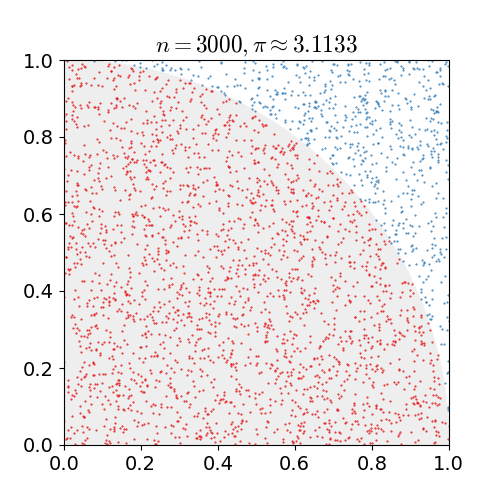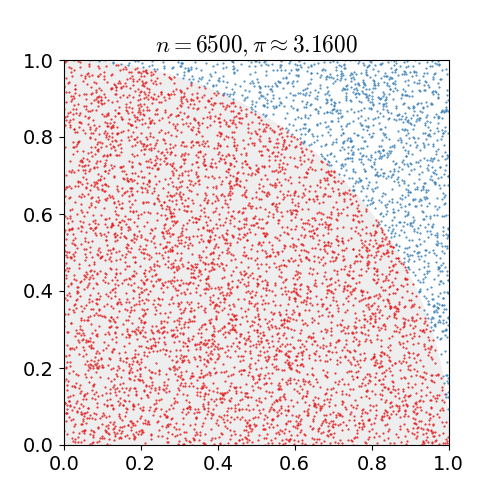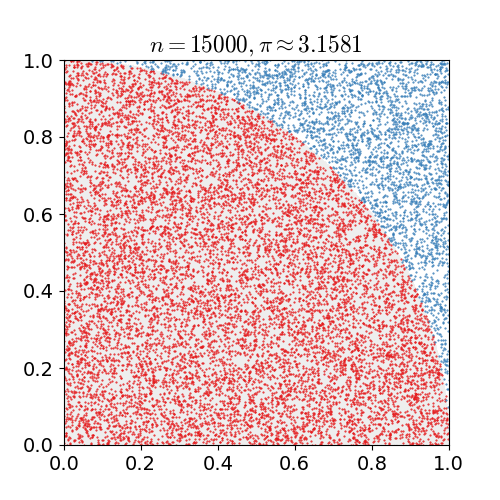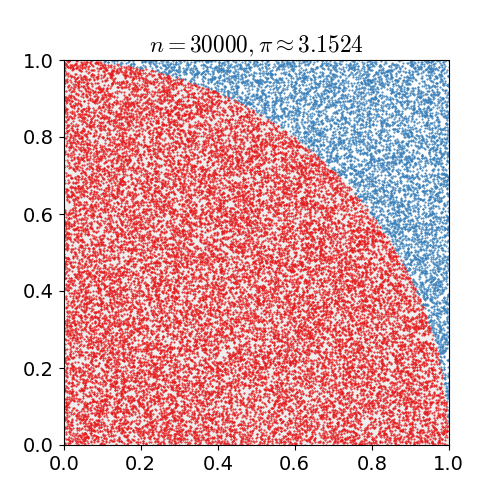
下面,我们来用几行简单的 Python 代码来模拟一下,
import numpy as np
import matplotlib.pyplot as plt
n = 5000
x = np.random.rand(n, 2)
inside = x[np.sqrt(x[:,0]2+x[:,1]2)<1]
estimate = 4*len(inside)/len(x)
print ('Estimate of pi:{}'.format(estimate))
plt.style.use("bmh")
plt.figure(figsize =(8,8))
plt.scatter(x[:, 0], x[:, 1], s=.85, c='red')
plt.scatter(inside[:, 0], inside[:, 1], s=.5, c='blue')
plt.show()
Estimate of pi:3.128
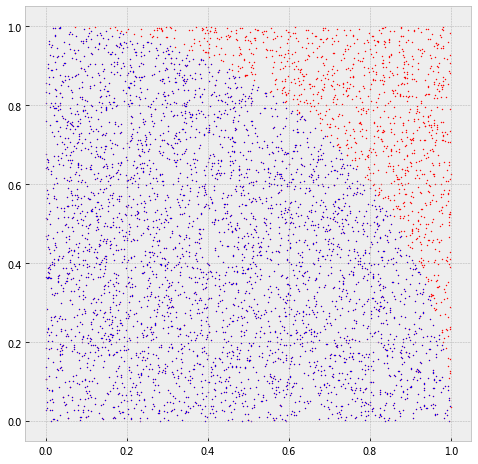
通常,蒙特卡罗方法涉及的采样方法可以分为三类,
直接采样。无需任何先验信息即可从分布中直接进行抽样。 重要性抽样。如果分布太复杂而无法从中进行采样时,则使用更简单的近似函数进行采样。这是贝叶斯优化和代理优化的核心思想。 拒绝采样。在满足某些标准的情况下接受采样点。将采样一个数据作为一个提议,通过一个接受概率来确定要不要接受这个提议。
第一类直接采样方法就是上面逼近形状面积的方法,而其他两类方法后续文章再作具体介绍。
2MCMC
通常可以在两种情况下使用蒙特卡罗采样:
优化问题。要找到最佳状态,就需要在探索(exploration)与开发(exploitation)之间保持一定平衡。当蒙特卡罗采样(探索)与另一种机制配合使用来控制开发,它可能是找到最优值的有力工具。 概率和函数逼近问题。蒙特卡罗采样法是一种间接评估某些概率或函数的很好方法,特别是当通过其他方法很难实现这点时。
由于蒙特卡罗方法的基本思想很简单,但是可能会以相当复杂和创造性的方式来使用,因此最好通过几个示例来揭示其思路。
首先,请考虑马尔可夫链蒙特卡罗(MCMC)方法,该方法尝试从目标分布生成随机样本,但是不知道分布具体是什么。马尔可夫链(Markov Chains)可以用于表示这些分布。具体来说,马尔可夫链是一个图,其中每个节点都是一个状态,以及转移到另一个状态的概率
考虑一下某个天气恶劣的城市,用马尔可夫链表示天气,假设那里的天气状况是风、冰雹/雪、雷暴或降雨。每天都可以根据当天天气来预测第二天的天气。例如,如果今天下雪,则明天有
要在马尔可夫链上遍历,我们从一个位置
如果我们经过大量时间(例如 10,000 个模拟天)遍历马尔可夫链,就会达到一种概率平衡。这意味着,根据大数定律,我们可以简单地基于我们遍历的节点状态中有多少在下雨来估计下雨的概率。
例如,如果通过马尔可夫链在 10,000 多个状态中转移收到了以下结果:
Wind 节点遍历 2754 次 Thunderstorm 节点遍历 1034 次 Hail/Snow 节点遍历 4301 次 Raining 节点遍历 1911 次
根据这个模型,我们可以得到如下概率:
P(Wind) = 0.2754 P(Thunderstorm) = 0.1034 P(Hail/Snow) = 0.4031 P(Raining) = 0.1911
然后,你可以简单地从分布中进行相应采样,即从马尔可夫链中以一定概率随机抽取一个状态,而无需动态遍历该状态。通过蒙特卡罗采样以后,即马尔可夫链的反复迭代和随机遍历,该系统能够折叠起来表示概率分布。
小结: 可以构造马尔可夫链来建模无法直接采样的复杂关系,然后对其进行简化以找到其潜在的概率分布。
有许多完善的 MCMC 算法,例如 Metropolis-Hastings 算法或 Gibbs 采样。都是试图对系统的潜在概率进行建模。
3应 用
要将理论投入到实际应用,可以看一下蒙特卡罗树搜索(MCTS),它是用于智力游戏的强化学习系统的关键部分。早期的游戏系统,例如 IBM 深蓝在 1997 年击败国际象棋冠军 加里·卡斯帕罗夫(Gary Kasparov)的最初胜利,是基于类似 minimax 的算法,该算法可以遍历基于当前局面的所有可能下法,并确定能够取得绝对胜利(或最高机率)的下法。
随着游戏变得更加复杂(最著名的是围棋游戏甚至是 DOTA 之类的射击游戏),遍历所有可能的场景在目前的计算力上是不可行时,也是不明智的。取而代之的是,明智的做法是让玩家利用已知动作来探索潜在的有益动作,同时放弃极有可能失败的动作。
让我们来像这样构造一棵树,其中每个节点代表某种游戏状态。可以通过采取某些行动在节点之间转移。从游戏的初始状态开始,我们可以采用几个可能的节点。

价值神经网络试图在每一步上都赋予价值: 给定这一步,智能体获胜的概率是多少?请注意,一开始,由于价值网络尚未经过训练,因此将给出随机的猜测。但是,随着系统经历足够多的游戏,它将可以更智能地分析某些动作的效果。

可以执行简单的加权蒙特卡罗采样,而不是简单地选择概率最高的节点。如果网络认为节点 2 将有 90% 的获胜机会,则它有更大的机会被选中,但仍然还是有可能会选择节点 3 和 1。该方式训练了一个如何选择潜在节点的策略。
其背后的逻辑是,某个动作的可预见价值受到可能性的限制(也许对手会做出意想不到的动作)。这样可能有利于发现会带来更多好处的动作,此外,仅仅利用已知动作而不冒险探索其他可能空间会导致竞争性和惰性模型的出现,这点是复杂的强化学习环境中并不希望看到的。
然后,被选中节点将进一步扩展,并重复该过程,直到游戏终止。将概率纳入决策制定过程中,而不是确定性地选择最佳价值,这有助于强化学习平衡开发和探索两者之间的取舍。
如果我们从统计学的角度来看这一点,则使用蒙特卡罗采样对最佳概率分布
蒙特卡罗树搜索(MCTS)是 DeepMind 开发的强化学习系统 AlphaGo 击败顶级围棋选手的功臣。此外,MCTS 在其他地方也具有广泛的应用。
模拟退火是蒙特卡罗方法的另一种应用,在寻找全局最优值的任务中充当非梯度函数优化的一种有效方法。像应用其他问题的蒙特卡罗方法一样,搜索空间是离散的,因为我们并不打算尝试优化连续值。
在那些以固定的时间内找到近似全局最优值比其精确值更有价值的问题中,模拟退火实际上可能比梯度下降之类的算法更可取。
模拟退火的思想来自冶金学,退火是对材料的受控加热或冷却,以增加其尺寸并消除缺陷。同样,模拟退火控制系统中的能量,这决定了在探索新可能性时愿意承担多少风险。
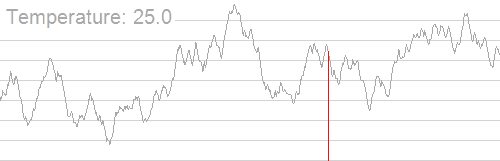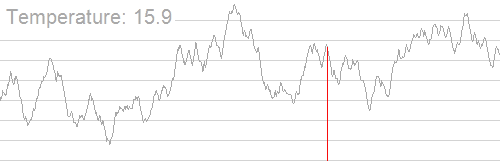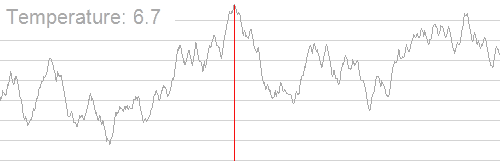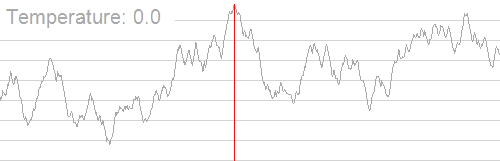
温度从某个初始值开始,这代表了各种计时器。在每个状态
当温度随着每个时间步长降低,模型的探索性就会降低,从而变得更具开发性。模拟退火允许从探索到开发的逐步过渡,这对于发现全局最优是非常有益的。
蒙特卡罗采样和贝叶斯方法用于对概率函数 Metropolis-Hastings 算法通常是将马尔可夫链蒙特卡罗方法用于查找转移阈值。这是自然的,因为模拟退火将解视为状态以及一种适合马尔可夫链建模的环境,并试图找到最佳的转移概率。
通常,蒙特卡罗方法或类似蒙特卡罗的方法会出现在我们最不期望的地方。尽管它是一种简单的机制,但它在无数的应用程序中都有着深厚而复杂的根源。
4小 结
蒙特卡罗方法基于以下思想: 将随机性引入系统通常可以有效地解决问题。 蒙特卡罗方法涉及的采样通常分为三类: 直接采样,重要性采样以及拒绝采样。 蒙特卡罗方法的两个常见应用包括优化以及对复杂概率和函数的估计。 在离散(非连续)以及确定性问题中,蒙特卡罗方法利用随机性+概率、大数定律以及高效采样框架来解决这些问题。 . 相关阅读 .
一个例子理解 AlphaGo 的技术原理
⟳参考资料⟲
Monte Carlo: https://en.wikipedia.org/wiki/Monte_Carlo_method
[2]Andre Ye: https://towardsdatascience.com/monte-carlo-methods-made-simple-91758ba58dde
[3]Christopher Pease: https://towardsdatascience.com/an-overview-of-monte-carlo-methods-675384eb1694
