Bootstrap方法在AB TEST中的应用
▐ 前言
实验样本量太小,即便可能存在效应也无法有效的检验出显著的效果 检验指标构造复杂,如两随机变量的商构造的指标,例如CTR=CLICK/PV,此处PV、CLICK均为随机变量,在计算CTR的方差时,需要采用不同的计算方法来近似计算方差。 样本数据倾斜严重,头部效应明显,个别样本会严重影响整体效果的差异。
▐ 基本思想
Where there is sample, there is uncertainty。
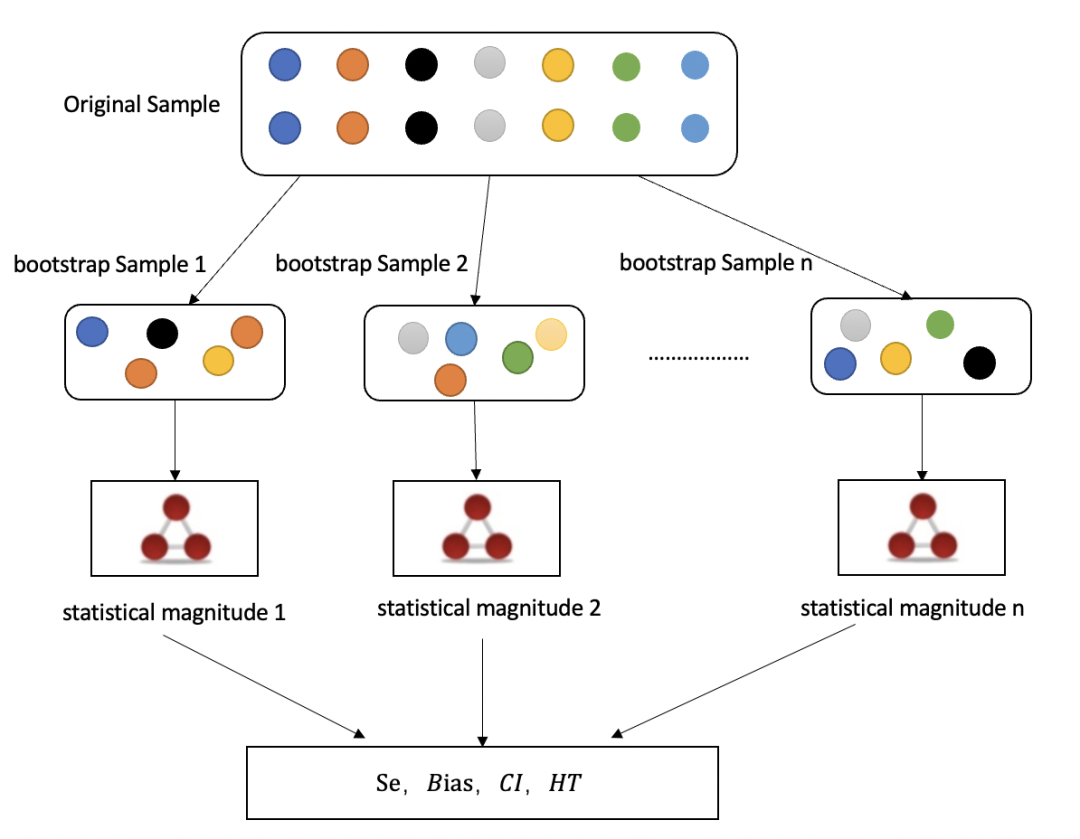
▐ 简单的推导过程
用 Bootstrap 来计算估计量的 SE, BIAS
前面讲过,Bootstrap 就是多次抽样,这样就得到了 Empirical dist. ,而我们的估计量则是 。我们先来看SE,考虑
我们使用 "Plug-in" Priniciple,则
其中的 为 B 个 Bootstrap 估计量的均值;分母用了B-1是为了无偏。于是我们得到了SE的 Bootstrap 估计公式
对于BIAS
用 Bootstrap 来计算估计量的 CI
我们主要介绍3种常用的 Bootstrap 计算 CI 的方法。
标准 Bootstrap(SB)
百分位数 Bootstrap(PB)
百分位数的 Bootstrap 直接用的分布来估计,我们通过 Bootstrap 构造了一个的分布,则实际的区间估计可以用的分位数直接进行估计,的置信区间为:
t百分位数Bootstrap(PTB)
结果比较
| 常规方法 | SB | PB | PTB | |
|---|---|---|---|---|
| 置信区间 | [1477,1503] | [1479,1502] | [1479,1502] | [1480,1502] |
| 宽度 | 26 | 23 | 23 | 22 |
▐ 应用实例

则
▐ Bootstrap&Jackknife
抽样方法不同。Bootstrap 采用的是「有放回抽样」,jackknife采用的是「无放回抽样」。 Jackknife 在解决不光滑 (Smooth) 参数估计时会失效,而 Bootstrap 可以解决这个问题,例如中位数,分位数等估计量。 若统计量是线性的,二者的结果会非常接近。虽然从表面上看,Jackknife 似乎只利用了非常有限的样本信息。对于非线性统计量而言,Jackknife 会有信息损失,此时 Bootstrap 较好。这是因为,Jackknife 可以视为 Bootstrap 的线性近似。换言之,Jackknife 的准确程度取决于统计量与其线性展开的接近程度。
▐ 总结
【阿里妈妈数据科学系列】持续更新,欢迎关注!
【阿里妈妈数据科学系列】第二篇:在线分流框架下的AB Test
【阿里妈妈数据科学系列】第三篇:离线抽样框架下的AB Test


评论
