数据分析教材系列:Numpy常用知识点汇总
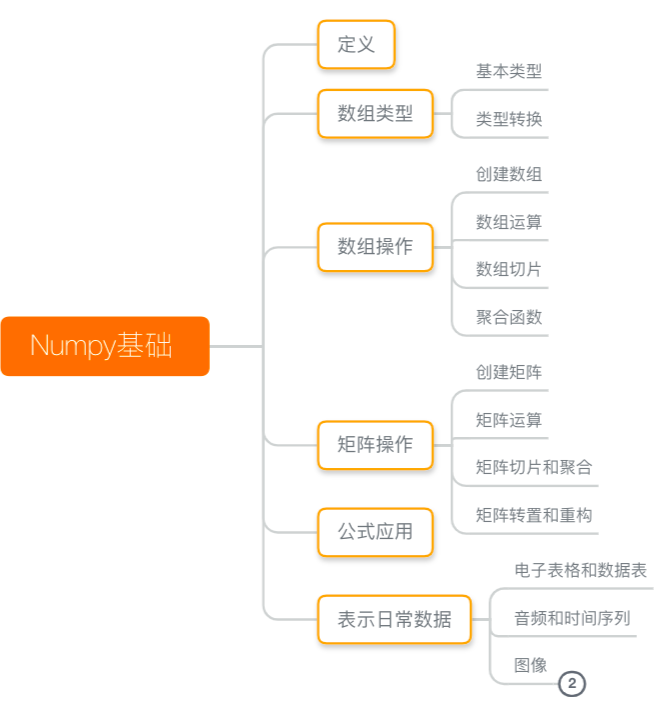
本文目录
基本类型

类型转换
j = np.arange(3)
print(j)
print('查看数据类型:\n',j.dtype)
print('-'*20)
g = j.astype('float') #转换为float类型
print('查看转换后类型:\n',g.dtype)
[0 1 2]
查看数据类型:
int64
--------------------
查看转换后类型:
float64
创建数组
#方法一、将列表或元组传入np.array()来创建
print(np.array([1,2,3]))
#方法二、初始化数组的值,只需传入元素个数即可
print(np.ones(3))
print(np.zeros(3))
print(np.random.random(3))
[1 2 3]
[1. 1. 1.]
[0. 0. 0.]
[0.71318806 0.95903425 0.75384478]
数组运算
#首先创建两个数组
data1 = np.array([1,2])
data2 = np.ones(2)
print(data1,data2)[1 2] [1. 1.]
#数组间加减乘除
jia = data1+data2
jian = data1-data2
cheng = data1*data2
chu = data1/data2
#数组与单个数值的操作
shuzhi1 = data1*100
shuzhi2 = data1/100
print(jia,jian,cheng,chu,shuzhi1,shuzhi2)
[2. 3.] [0. 1.] [1. 2.] [1. 2.] [100 200] [0.01 0.02]
数组切片
#类似列表操作进行索引和切片
data3 = np.array([1,2,3,4,5])
print(data3)
print(data3[0])
print(data3[2:4])
print(data3[2:])
print(data3[:4])
[1 2 3 4 5]
1
[3 4]
[3 4 5]
[1 2 3 4]
聚合函数
data4 = np.array([1,2,3,4,5])
print(data4.max()) #最大值
print(data4.min()) #最小值
print(data4.mean()) #均值
print(data4.sum()) #求和
print(data4.std()) #标准差
5
1
3.0
15
1.4142135623730951
创建矩阵
#方法一、通过将二维列表传给Numpy来创建矩阵
print(np.array([[1,2],[3,4]]))
#方法二、传入一个元组来描述矩阵的维度
print(np.ones((3,2))) #3行2列矩阵
print(np.zeros((3,2)))
print(np.random.random((3,2)))
[[1 2]
[3 4]]
[[1. 1.]
[1. 1.]
[1. 1.]]
[[0. 0.]
[0. 0.]
[0. 0.]]
[[0.2928769 0.24093443]
[0.06189287 0.62359846]
[0.80539105 0.81706549]]
矩阵运算
#相同大小矩阵的加减乘除
data5 = np.array([[1,2],[3,4]])
data6 = np.ones((2,2))
jia1 = data5 + data6
cheng1 = data5 * data6
print(jia1,'\n',cheng1)
[[2. 3.]
[4. 5.]]
[[1. 2.]
[3. 4.]]
#不同大小矩阵的加减乘除(仅两个矩阵秩数为1时)
data7 = np.array([[1,2],[3,4],[5,6]])
data8_1 = np.ones((1,2)) #行秩为1
data8_2 = np.ones((3,1)) #列秩为1
print(data7 + data8_1)
print('-'*20)
print(data7 + data8_2)
[[2. 3.]
[4. 5.]
[6. 7.]]
--------------------
[[2. 3.]
[4. 5.]
[6. 7.]]
#矩阵乘法,dot()方法
data9 = np.array([[1,2,3]]) #1*3的矩阵
data10 = np.array([[1,2],[3,4],[5,6]]) #3*2的矩阵
data11 = data9.dot(data10) #1*2的矩阵
print(data11)
[[22 28]]
矩阵切片和聚合
#可以在不同维度上使用索引操作来对数据进行切片
data12 = np.array([[1,2],[3,4],[5,6]])
print(data12)
print(data12[0,1]) #1行2列数据
print(data12[1:3]) #2-3行
print(data12[0:2,0]) #1-2行,1列
[[1 2]
[3 4]
[5 6]]
2
[[3 4]
[5 6]]
[1 3]
#可以像聚合向量一样聚合矩阵
print(data12.max())
print(data12.min())
print(data12.sum())
print(data12.mean())
print(data12.std())
#还可以使用axis参数指定行和列的聚合
print(data12.max(axis = 0)) #纵向执行
print(data12.max(axis = 1)) #横向执行
6
1
21
3.5
1.707825127659933
[5 6]
[2 4 6]
矩阵转置和重构
#NumPy数组的属性T可用于获取矩阵的转置
print('转置前:\n',data12)
print('转置后:\n',data12.T)
转置前:
[[1 2]
[3 4]
[5 6]]
转置后:
[[1 3 5]
[2 4 6]]
In:
#在较为复杂的用例中,可能需要使用NumPy的reshape()方法改变某个矩阵的维度
data13 = np.array([1,2,3,4,5,6])
print('重构前:\n',data13)
print('重构后:\n',data13.reshape(2,3))
print('重构后:\n',data13.reshape(3,2))
Out:
重构前:
[1 2 3 4 5 6]
重构后:
[[1 2 3]
[4 5 6]]
重构后:
[[1 2]
[3 4]
[5 6]]
In:
#上文中的所有功能都适用于多维数据,其中心数据结构称为ndarray(N维数组)
data14 = np.array([[[1,2],[3,4]],[[5,6],[7,8]]])
print(data14)
print('-'*20)
#改变维度只需在NumPy函数的参数中添加一个逗号和维度
print(np.ones((4,3,2)))
print('-'*20)
print(np.zeros((4,3,2)))
print('-'*20)
print(np.random.random((4,3,2)))
Out:
[[[1 2]
[3 4]]
[[5 6]
[7 8]]]
--------------------
[[[1. 1.]
[1. 1.]
[1. 1.]]
[[1. 1.]
[1. 1.]
[1. 1.]]
[[1. 1.]
[1. 1.]
[1. 1.]]
[[1. 1.]
[1. 1.]
[1. 1.]]]
--------------------
[[[0. 0.]
[0. 0.]
[0. 0.]]
[[0. 0.]
[0. 0.]
[0. 0.]]
[[0. 0.]
[0. 0.]
[0. 0.]]
[[0. 0.]
[0. 0.]
[0. 0.]]]
--------------------
[[[0.37593802 0.42651876]
[0.74639264 0.19783467]
[0.787414 0.63820259]]
[[0.84871262 0.46467497]
[0.54633954 0.4376995 ]
[0.71988166 0.9306682 ]]
[[0.6384108 0.74196991]
[0.73857164 0.38450555]
[0.68579442 0.64018511]]
[[0.60382775 0.35889667]
[0.8625612 0.86523028]
[0.83701853 0.08289658]]]

In:
#在NumPy中可以很容易地实现均方误差。
np_1 = np.ones(3)
np_2 = np.array([1,2,3])
error = (1/3) * np.sum(np.square(np_1 - np_2))
print(error)
Out:
1.6666666666666665
电子表格和数据表

音频和时间序列

图像

黑白图像

彩色图像
相关阅读:
评论
