用数学的语言观察与思考
日期:2020年08月10日
正文共:4912字6图
预计阅读时间:13分钟
来源:人民邮电出版社
辛普森审判


纯粹数学的精华
无限世界

欢迎来到加州旅馆!加州旅馆拥有无穷间客房。您随时都可以入住。
经理(以下称为“经”):欢迎来到加州旅馆!我是经理戴维·希尔伯特。本旅馆随时都有空房,因为我们拥有无穷间客房。您看走廊的前方,每间客房都标有房号,1、2、3 · · · 永远不会停止。您看起来很疲惫!我马上让客房部主管为您准备房间。
客房部主管(以下称为“主”):经理,请您不要再轻易许诺说有多余房间了。今天客房已满,无法为客人办理入住。
经:你不用担心,把室内广播的话筒递给我。(拿起话筒)“不好意思打扰各位休息了。请1 号房的客人搬到2 号房,2号房的客人搬到3 号房”。
主:1 号房就变成空房了。
经:那么,就请这位客人入住1 号房。加州旅馆的卖点就是保证您随时都可以入住。
主:驶来了一辆旅游大巴,车身贴着“自然数旅行团”的标签。
经:你数一下来了多少客人。
主:1、2、3 · · ·,怎么也数不完。貌似所有自然数都来了,总共有无穷位客人。而且客房已满,如果只来1 位或2 位还可以想想办法。现在来了无穷位客人,客房肯定不够了。
经:你不用担心。又到了室内广播的时间,“不好意思打扰各位休息了。现在麻烦各位搬到偶数房间。请1 号房的客人搬到2 号房,2 号房的客人搬到4 号房。3 号房的客人搬到6 号房。”
主:1 号房、3 号房、5 号房· · · 等奇数房间全部空出来了。
经:请大巴上的客人按顺序入住。第一位客人入住1 号房、第2 为客人入住3 号房、第n 位客人入住(2n − 1) 号房。这样一来,就能帮乘坐大巴的所有自然数客人安排房间。加州旅馆的卖点就是保证您随时都可以入住。
主:经理,又来了好几辆自然数旅游大巴。
经:你先数好大巴数。
主:1、2、3 · · · 怎么也数不完。貌似来了无穷辆大巴。而且,每辆大巴内都坐着无穷位客人。客房肯定不够了。
经:你不用担心。按照到达旅馆的先后顺序给旅游大巴编号,1、2、3 · · · 再播放与刚才相同的广播内容。
主:和刚才一样,奇数房间都空出来了。但是,也只够一辆旅游大巴的客人入住。
经:你不用担心。旅游大巴里的客人都有2 个号码,一个是自己乘坐的大巴编号,一个是自己在大巴里的座号。例如,如果是3 号大巴的第5 名乘客,就记作(3, 5)。
主:不过经理,1 号大巴的客人全部入住后,客房就全满了。
经:像你这样安排的话当然会住不下。首先,请客人们按我说的排队。
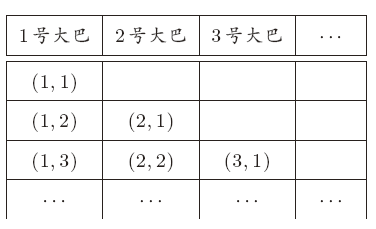
主:麻烦客人们排一下队伍。请2 号大巴的客人后退一步,3 号大巴的客人后退2 步。
经:对了,等客人们排好队后,给他们发放新的号码牌。
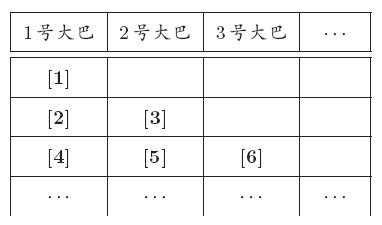
主:请按从前到后,从左到右的顺序传递号码牌。
经:这样一来,每位客人都能拿到号码牌。然后我们只要按照新的号码牌安排房间即可。刚才已经请之前入住的客人都搬到偶数房间,所以现在奇数房间都空出来了。那么,请[1] 号客人入住1 号房,[2] 号客人入住3 号房,[n] 号客人入住(2n − 1) 号房。
主:即使来了无穷多辆大巴的客人,也能完美地安排他们入住。
经:加州旅馆的卖点就是保证您随时都可以入住。
主:又来了一辆大巴,是有理数旅游团。
经:你不用担心。加州旅馆随时都有房间。
主:这次来的客人是分数。
经:所有的分数都来了吗?
主:是的。仅1 和2 之间的分数就是无穷个,看起来比旅馆的房间还要多,能住得下吗?
经:你不用担心。刚才拿着大巴编号和座位编号2 个数字的客人都已经顺利入住了。
主:是的,给这些客人发放了新的号码牌,例如(1, 2) 换成[2],(2, 3) 换成[8],然后让他们按照新号码牌先后办理了入住。
经:只要把分数看成2 的数对就好了。例如客人1/2 就是(1, 2),给他发放[2] 号,客人2/3 就是(2, 3),换成[8]号。然后按照刚才的方法安排他们入住。
主:不过1/2 = 2/4,客人1/2 拿到的是[2] 号,而客人2/4 拿到的却是[8] 号。说起来,1/2 = 3/6 = 4/8 = 5/10 =· · ·,所以重复的客人太多了。
经:那就把重复的房间空出来。
主:这家旅馆太厉害了。分数的客人全部成功入住,而且还有空房。
经:时间不早了,我先去休息了。剩下的就交给你处理了。
主:(原来如此!不管来多少客人,只要给他们分配号码牌就可以了。如果我能处理好,经理一定会对我刮目相看。客人们快点来吧!)
导游(以下称为“导”):这么晚还来打搅你们,真是不好意思。我是实数旅行团的导游。
。
。
。
【注】这段对话是1924 年希尔伯特在哥廷根大学讲课时,为说明有限集合和无限集合的区别而使用的例子,被叫作“希尔伯特旅馆”。
— THE END —

