【机器学习】全面解析Kmeans聚类算法(Python)
一、聚类简介
Clustering (聚类)是常见的unsupervised learning (无监督学习)方法,简单地说就是把相似的数据样本分到一组(簇),聚类的过程,我们并不清楚某一类是什么(通常无标签信息),需要实现的目标只是把相似的样本聚到一起,即只是利用样本数据本身的分布规律。
聚类算法可以大致分为传统聚类算法以及深度聚类算法:
传统聚类算法主要是根据原特征+基于划分/密度/层次等方法。
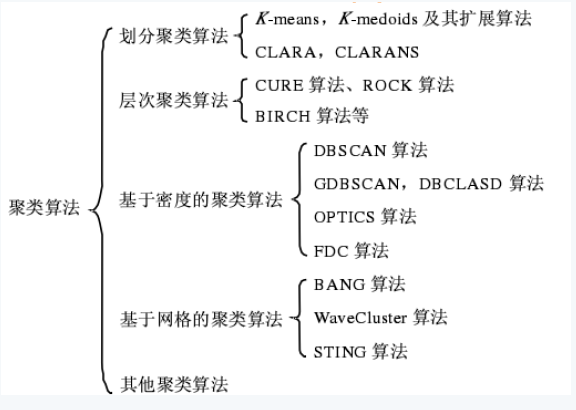
深度聚类方法主要是根据表征学习后的特征+传统聚类算法。 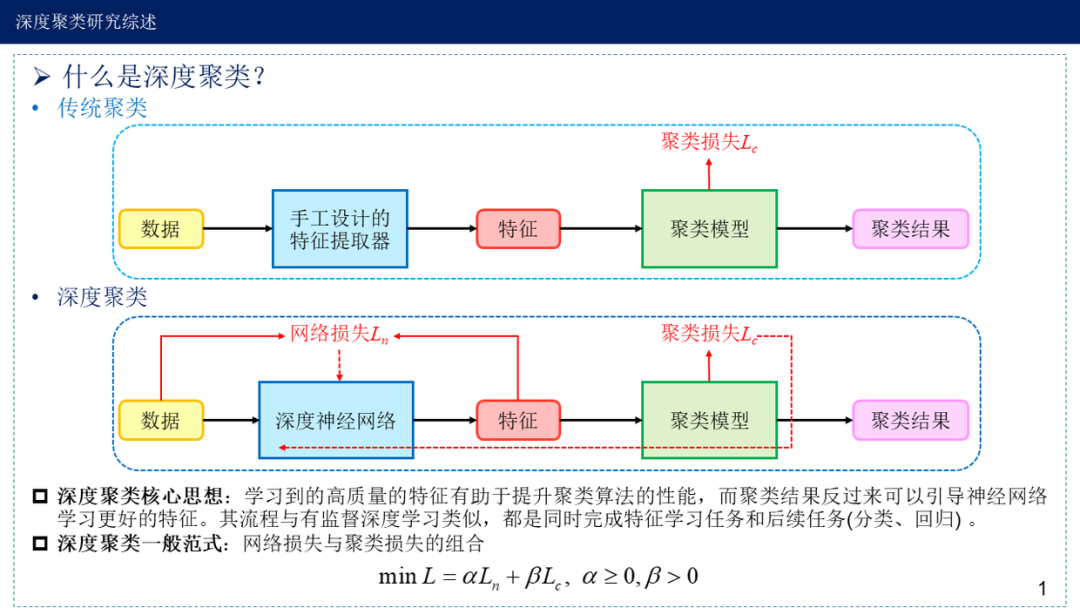
二、kmeans聚类原理
kmeans聚类可以说是聚类算法中最为常见的,它是基于划分方法聚类的,原理是先初始化k个簇类中心,基于计算样本与中心点的距离归纳各簇类下的所属样本,迭代实现样本与其归属的簇类中心的距离为最小的目标(如下目标函数)。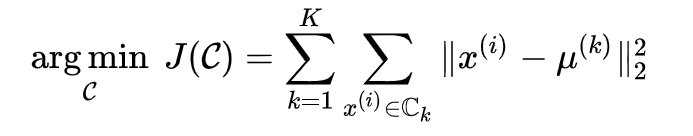
其优化算法步骤为:
1.随机选择 k 个样本作为初始簇类中心(k为超参,代表簇类的个数。可以凭先验知识、验证法确定取值);
2.针对数据集中每个样本 计算它到 k 个簇类中心的距离,并将其归属到距离最小的簇类中心所对应的类中;
3.针对每个簇类,重新计算它的簇类中心位置;
4.重复迭代上面 2 、3 两步操作,直到达到某个中止条件(如迭代次数,簇类中心位置不变等)。
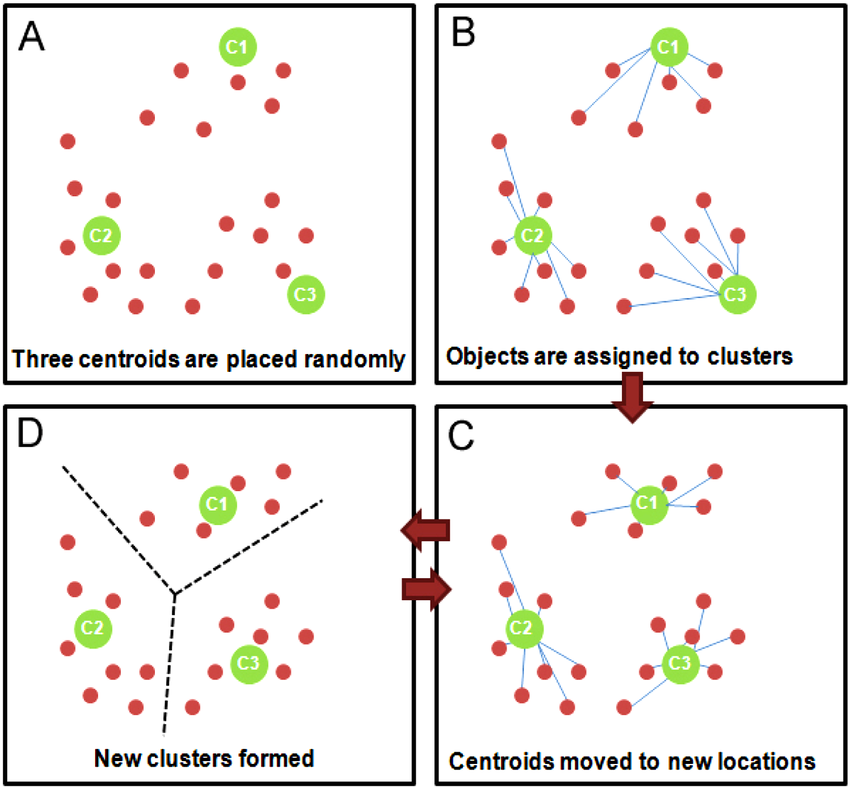
....完整代码可见:https://github.com/aialgorithm/Blog 或文末阅读原文
#kmeans算法是初始化随机k个中心点
random.seed(1)
center = [[self.data[i][r] for i in range(1, len((self.data)))]
for r in random.sample(range(len(self.data)), k)]
#最大迭代次数iters
for i in range(self.iters):
class_dict = self.count_distance() #计算距离,比较个样本到各个中心的的出最小值,并划分到相应的类
self.locate_center(class_dict) # 重新计算中心点
#print(self.data_dict)
print("----------------迭代%d次----------------"%i)
print(self.center_dict) #聚类结果{k:{{center:[]},{distance:{item:0.0},{classify:[]}}}}
if sorted(self.center) == sorted(self.new_center):
break
else:
self.center = self.new_center
...
可见,Kmeans 聚类的迭代算法实际上是 EM 算法,EM 算法解决的是在概率模型中含有无法观测的隐含变量情况下的参数估计问题。
在 Kmeans 中的隐变量是每个类别所属类别。Kmeans 算法迭代步骤中的 每次确认中心点以后重新进行标记 对应 EM 算法中的 E 步 求当前参数条件下的 Expectation 。而 根据标记重新求中心点 对应 EM 算法中的 M 步 求似然函数最大化时(损失函数最小时)对应的参数 。EM 算法的缺点是容易陷入局部极小值,这也是 Kmeans 有时会得到局部最优解的原因。
三、选择距离度量
kmeans 算法是基于距离相似度计算的,以确定各样本所属的最近中心点,常用距离度量有曼哈顿距离和欧式距离,具体可以见文章【全面归纳距离和相似度方法(7种)】
曼哈顿距离 公式:
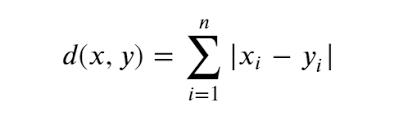
欧几里得距离 公式:
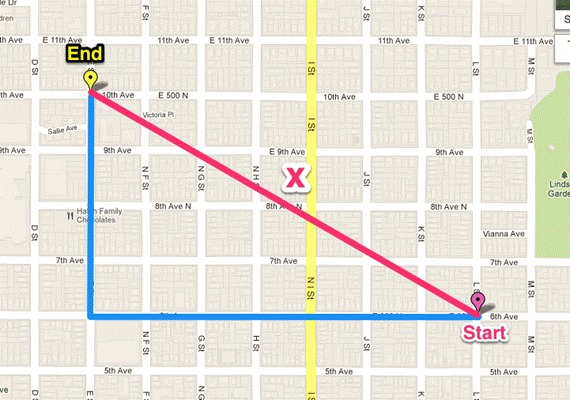
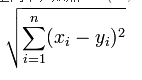 曼哈顿、欧几里得距离的计算方法很简单,就是计算两样本(x,y)的各个特征i间的总距离。如下图(二维特征的情况)蓝线的距离即是曼哈顿距离(想象你在曼哈顿要从一个十字路口开车到另外一个十字路口实际驾驶距离就是这个“曼哈顿距离”,也称为城市街区距离),红线为欧几里得距离:
曼哈顿、欧几里得距离的计算方法很简单,就是计算两样本(x,y)的各个特征i间的总距离。如下图(二维特征的情况)蓝线的距离即是曼哈顿距离(想象你在曼哈顿要从一个十字路口开车到另外一个十字路口实际驾驶距离就是这个“曼哈顿距离”,也称为城市街区距离),红线为欧几里得距离:
四、k 值的确定
kmeans划分k个簇,不同k的情况,算法的效果可能差异就很大。K值的确定常用:先验法、手肘法等方法。
先验法
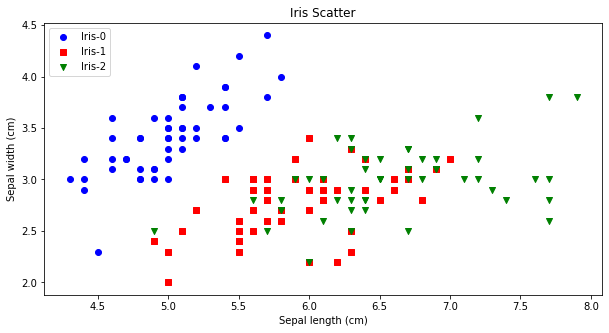
先验比较简单,就是凭借着业务知识确定k的取值。比如对于iris花数据集,我们大概知道有三种类别,可以按照k=3做聚类验证。从下图可看出,对比聚类预测与实际的iris种类是比较一致的。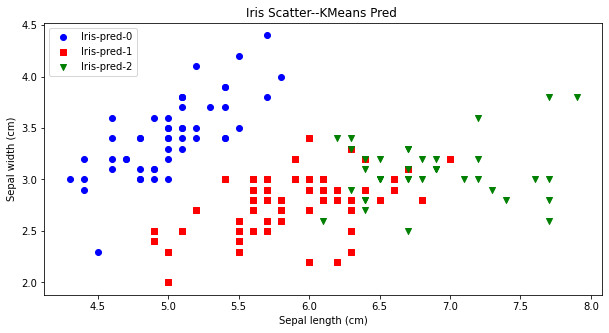
手肘法
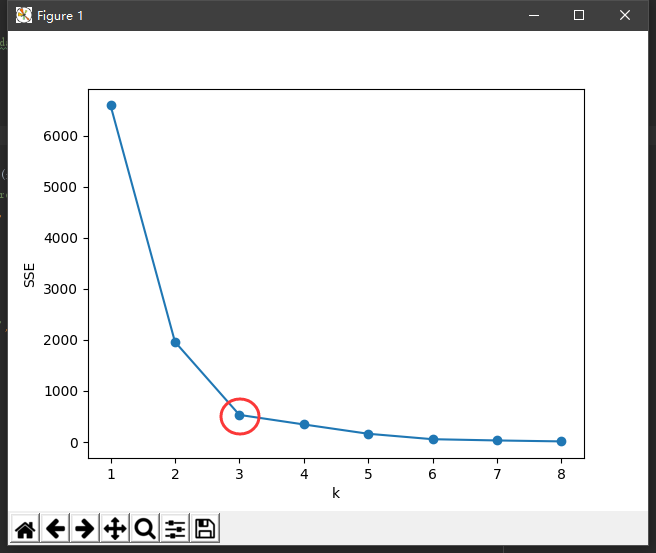
手肘法的缺点在于需要人为判断不够自动化,还有些其他方法如:
使用 Gap statistic 方法,确定k值。 验证不同K值的平均轮廓系数,越趋近1聚类效果越好。 验证不同K值的类内距离/类间距离,值越小越好。 ISODATA算法:它是在k-均值算法的基础上,增加对聚类结果的“合并”和“分裂”两个操作,确定最终的聚类结果。从而不用人为指定k值。
五、Kmeans的缺陷
5.1 初始化中心点的问题
kmeans是采用随机初始化中心点,而不同初始化的中心点对于算法结果的影响比较大。所以,针对这点更新出了Kmeans++算法,其初始化的思路是:各个簇类中心应该互相离得越远越好。基于各点到已有中心点的距离分量,依次随机选取到k个元素作为中心点。离已确定的簇中心点的距离越远,越有可能(可能性正比与距离的平方)被选择作为另一个簇的中心点。如下代码。
# Kmeans ++ 算法基于距离概率选择k个中心点
# 1.随机选择一个点
center = []
center.append(random.choice(range(len(self.data[0]))))
# 2.根据距离的概率选择其他中心点
for i in range(self.k - 1):
weights = [self.distance_closest(self.data[0][x], center)
for x in range(len(self.data[0])) if x not in center]
dp = [x for x in range(len(self.data[0])) if x not in center]
total = sum(weights)
#基于距离设定权重
weights = [weight/total for weight in weights]
num = random.random()
x = -1
i = 0
while i < num :
x += 1
i += weights[x]
center.append(dp[x])
center = [self.data_dict[self.data[0][center[k]]] for k in range(len(center))]
5.2 核Kmeans
基于欧式距离的 Kmeans 假设了了各个数据簇的数据具有一样的的先验概率并呈现球形分布,但这种分布在实际生活中并不常见。面对非凸的数据分布形状时我们可以引入核函数来优化,这时算法又称为核 Kmeans 算法,是核聚类方法的一种。核聚类方法的主要思想是通过一个非线性映射,将输入空间中的数据点映射到高位的特征空间中,并在新的特征空间中进行聚类。非线性映射增加了数据点线性可分的概率,从而在经典的聚类算法失效的情况下,通过引入核函数可以达到更为准确的聚类结果。
5.3 特征类型
kmeans是面向数值型的特征,对于类别特征需要进行onehot或其他编码方法。此外还有 K-Modes 、K-Prototypes 算法可以用于混合类型数据的聚类,对于数值特征簇类中心我们取得是各特征均值,而类别型特征中心取得是众数,计算距离采用海明距离,一致为0否则为1。
5.4 特征的权重
聚类是基于特征间距离计算,计算距离时,需要关注到特征量纲差异问题,量纲越大意味这个特征权重越大。假设各样本有年龄、工资两个特征变量,如计算欧氏距离的时候,(年龄1-年龄2)² 的值要远小于(工资1-工资2)² ,这意味着在不使用特征缩放的情况下,距离会被工资变量(大的数值)主导。因此,我们需要使用特征缩放来将全部的数值统一到一个量级上来解决此问题。通常的解决方法可以对数据进行“标准化”或“归一化”,对所有数值特征统一到标准的范围如0~1。
归一化后的特征是统一权重,有时我们需要针对不同特征赋予更大的权重。假设我们希望feature1的权重为1,feature2的权重为2,则进行0~1归一化之后,在进行类似欧几里得距离(未开根号)计算的时候,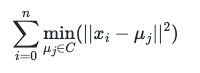 我们将feature2的值乘根号2就可以了,这样feature2对应的上式的计算结果会增大2倍,从而简单快速的实现权重的赋权。如果使用的是曼哈顿距离,特征直接乘以2 权重也就是2 。
我们将feature2的值乘根号2就可以了,这样feature2对应的上式的计算结果会增大2倍,从而简单快速的实现权重的赋权。如果使用的是曼哈顿距离,特征直接乘以2 权重也就是2 。
如果类别特征进行embedding之后的特征加权,比如embedding为256维,则我们对embedding的结果进行0~1归一化之后,每个embedding维度都乘以 根号1/256,从而将这个类别全部的距离计算贡献规约为1,避免embedding size太大使得kmeans的聚类结果非常依赖于embedding这个本质上是单一类别维度的特征。
5.5 特征的选择
kmeans本质上只是根据样本特征间的距离(样本分布)确定所属的簇类。而不同特征的情况,就会明显影响聚类的结果。当使用没有代表性的特征时,结果可能就和预期大相径庭!比如,想对银行客户质量进行聚类分级:交易次数、存款额度就是重要的特征,而如客户性别、年龄情况可能就是噪音,使用了性别、年龄特征得到的是性别、年龄相仿的客户!
对于无监督聚类的特征选择:
一方面可以结合业务含义,选择贴近业务场景的特征。
另一方面,可以结合缺失率、相似度、PCA等常用的特征选择(降维)方法可以去除噪音、减少计算量以及避免维度爆炸。再者,如果任务有标签信息,结合特征对标签的特征重要性也是种方法(如xgboost的特征重要性,特征的IV值。)
最后,也可以通过神经网络的特征表示(也就深度聚类的思想。后面在做专题介绍),如可以使用word2vec,将高维的词向量空间以低维的分布式向量表示。
- END -参考文献:
1、https://www.bilibili.com/video/BV1H3411t7Vk?spm_id_from=333.999.0.0
2、https://zhuanlan.zhihu.com/p/407343831
3、https://zhuanlan.zhihu.com/p/78798251
文章首发公众号“算法进阶”,文末阅读原文可访问文章相关代码
往期精彩回顾 本站qq群955171419,加入微信群请扫码:
