5分钟带你读「大清」微积分!160多年前清朝数学家撰写文言文版高等数学

新智元报道

新智元报道
编辑:小咸鱼 好困
【新智元导读】你有见过160多年前清朝数学家写的微积分书吗?这可能是最难懂的高数教材了,堪称天书!近日,网上流传着一本清朝的微积分课本,其中的所有数学表达式都是用文言文书写的。小编不才,斗胆翻译了一下,看看这天书里面到底写了些什么。
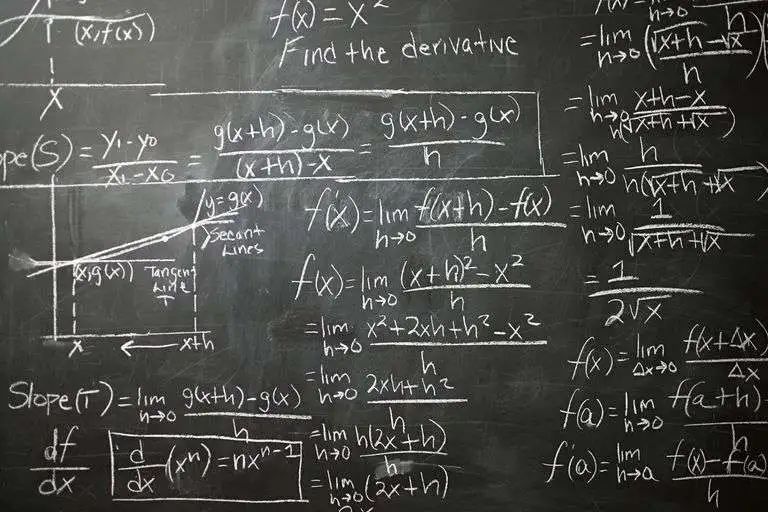



5分钟带你读清朝微积分
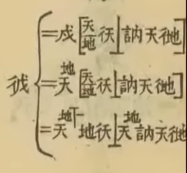
「分数」的「分子」是分母,「分母」是分子 。也就是说,如果看到「分数」,则它的倒数就是现代意义下的分数。
彳= d, 天 = x, 戍 = y,那么彳天 = dx, 彳戍 = dy
一 = 1
訥 = ln
丄 = +
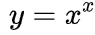 。
。
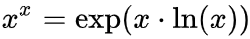 。
。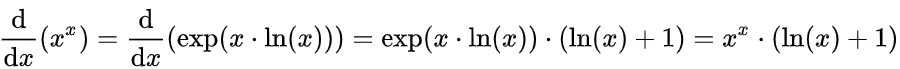
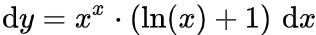
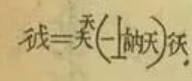

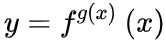 求导。
求导。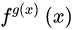 改写为:
改写为: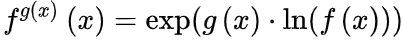 。
。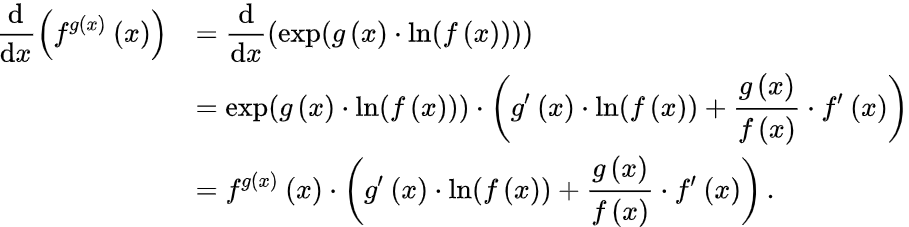
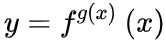 代入式子,将dx换到右边:
代入式子,将dx换到右边: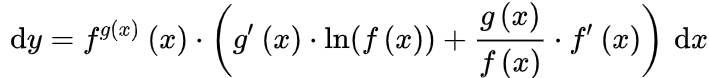
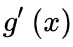 、
、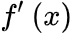 合并变成dg和df,所以:
合并变成dg和df,所以: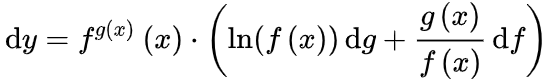
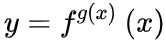 除到左边:
除到左边: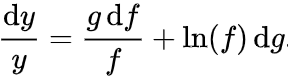

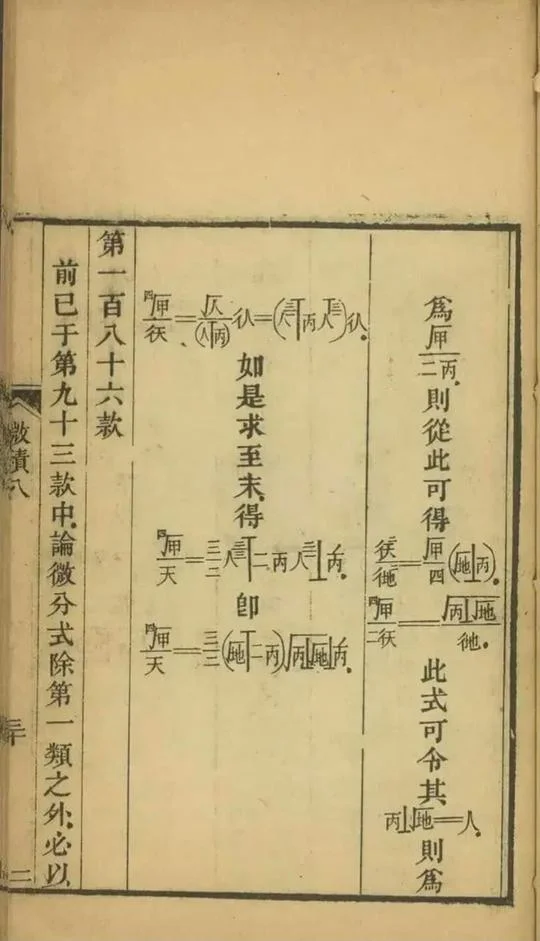
中国第一本微积分课本
中国第一本微积分课本


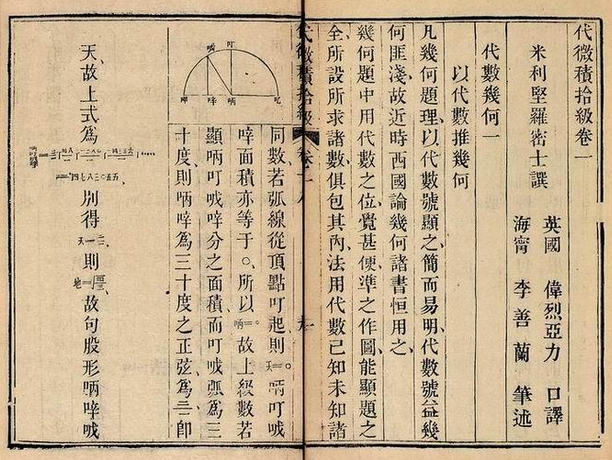
「微分积分,为中土算书所未有,然观当代天算家,如董方立氏、项梅侣氏、徐君青氏、戴鄂士氏、顾尚之氏,暨李君秋纫,所著各书,其理有什近微分者,因不用代数式,或言之甚繁推之甚难,今特偕李君译此书,为微分积分入门之助。」
「函数与变数之比例,俱谓之微分,用ㄔ号记之。如戌 = 天三,则得比例ㄔ天 : ㄔ戌 :: 一 : 三天二。ㄔ天、ㄔ戌为天与戊之微分。后皆仿此。用表天与戌之变比例,以一、四两率相乘,二、三两率相乘则得ㄔ戌 = 三天二ㄔ天,此显函数戌之变比例,等于三天乘变数天之变比例,以ㄔ天约之得ㄔ天/ㄔ戌 = 三天二。此显变数之变比例约函数之变比例,等于函数之微系数也。」
「积分为微分之还原,其法之要在识别微分所由生之函数,如已得天二之微分为二天ㄔ天,则有二天ㄔ天即知所由生之函数为天二,而天二即为积分。已得微分所由生之函数为积分,而积分或有常数附之,或无常数附之,既不能定,故式中恒附以常数,命为口丙,口丙或有同数或为0,须考题乃知。来本之视微分若函数诸小较之一,诸小较并之,即成函数,故微分之左系一禾字,指欲取诸微分之积分也。如下式禾二天ㄔ天=天+口丙。来氏说,今西国天算家大率不用,而惟用此禾字取其一览了然也。」

参考资料:
https://www.bilibili.com/video/BV1RR4y1t7AH?from=search&seid=8170464341069800644&spm_id_from=333.337.0.0
https://www.reddit.com/r/China_irl/comments/r0xh97/清朝微积分课本/
https://highscope.ch.ntu.edu.tw/wordpress/?p=25200
本文引用了以下知乎作者的文章:
「zdr0」https://zhuanlan.zhihu.com/p/437864462

评论
