二叉搜索树删除节点 动画演示
Day60:删除二叉搜索树的某个节点
1 题目
给定一个二叉搜索树的根节点 root 和一个值 key,删除二叉搜索树中的 key 对应的节点,并保证二叉搜索树的性质不变。返回二叉搜索树(有可能被更新)的根节点的引用。
一般来说,删除节点可分为两个步骤:
首先找到需要删除的节点; 如果找到了,删除它。
说明:要求算法时间复杂度为 O(h),h 为树的高度。
示例:
root = [5,3,6,2,4,null,7]
key = 3
5
/ \
3 6
/ \ \
2 4 7
给定需要删除的节点值是 3,所以我们首先找到 3 这个节点,然后删除它。
一个正确的答案是 [5,4,6,2,null,null,7], 如下图所示。
5
/ \
4 6
/ \
2 7
另一个正确答案是 [5,2,6,null,4,null,7]。
5
/ \
2 6
\ \
4 7
2 分析过程
这道题被leetcode定为中等难度级别,实话讲确实属于这类级别,虽然思路不难,但是要想一次写出准确无误的代码,仍然不是一件简单的事情。如果你第一次做这道题能很快写出来,说明你对递归的理解、指针的掌控都达到了一定水平。
这道题的思路很straitforward,根据BST的性质,具体说来分为如下几种情况:
如果被删除节点关键码key小于当前根节点nodei.val,则问题规模直接降阶到左子树中
关键码key大于当前根节点nodei.val,直接到右子树中查找
key等于当前根节点nodei.val,又分为4种情况:
(1). nodei 无左右子树,摘除nodei节点,等于直接返回 None
(2). nodei 仅有左子树,摘除nodei节点,等于直接返回 nodei.left
(3). nodei 仅有右子树,摘除nodei节点,等于直接返回 nodei.right
(4). nodei 都有左右子树,麻烦一点,方法之一:选择以nodei.right为根节点的树中最左侧节点,然后替换nodei
最后返回 nodei.
你看,上面的思路应该足够清晰,但是兑现为代码绝对又是另一回事。你首先要对递归有深刻的理解,其次像链表、二叉树等这类具备递归的数据结构,操作它们节点引用问题要时刻保持清醒,很容易出错。
3 如何写出代码
老规矩,这是我们的节点定义:
# Definition for a binary tree node.
# class TreeNode(object):
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = None
解决方案对象的主方法,调用自定义方法self.__delNodei(root,key),这个方法的构思思路是这样:
第一个参数是BST树中的任意节点,因为BST严格满足递归,所以选取任意一个以节点nodei为根的树,删除里面等于key的节点。因此,这个功能一旦实现后,只需在参数赋值时赋值它为root即可。
class Solution(object):
def deleteNode(self, root, key):
"""
:type root: TreeNode
:type key: int
:rtype: TreeNode
"""
return self.__delNodei(root,key)
所以关键是如何写出def __delNodei(self,nodei,key)方法,下面我们一步一步分析。
根据上面的4种情况分析,我们在情况4时会用到找树的最左节点,为此先写出这个方法def __findMinNode(self,nodei):
# 找到以nodei为根节点树的最小值
def __findMinNode(self,nodei):
if not nodei.left:
return nodei
while nodei.left:
nodei = nodei.left
return nodei
这个比较简单,是链表、二叉树等递归结构的常规迭代思路,注意与向量表i=i+1迭代思路的区别。
先写出第一种大情况,比较简单。因为方法self.__delNodei(nodei.left,key)实现删除等于key的节点后返回对nodei.left节点的引用,所以将nodei的left域指向它即可。
# 假定已经查询到nodei节点,删除后返回nodei节点的引用
def __delNodei(self,nodei,key):
if not nodei:
return None
#若满足下面条件,一定在左子树
if key < nodei.val:
nodei.left = self.__delNodei(nodei.left,key) # 删除后返回nodei.left节点的引用
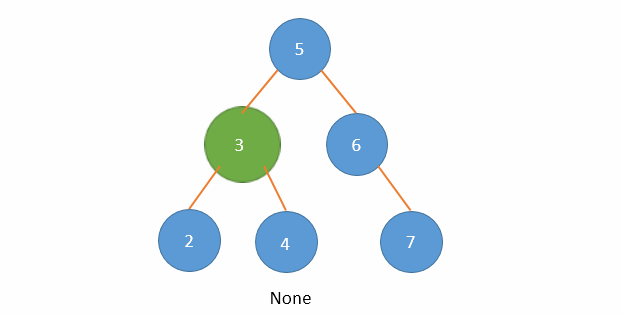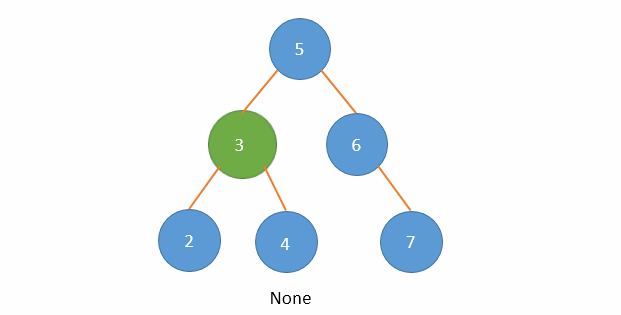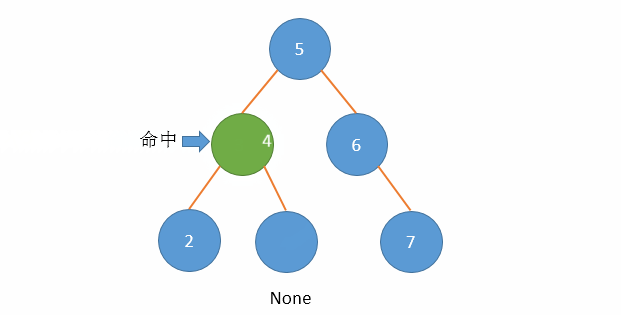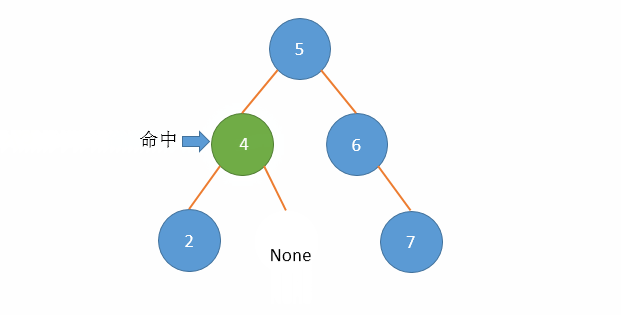
以下面二叉搜索树删除值等于3的节点为例演示,伸入到左子树:
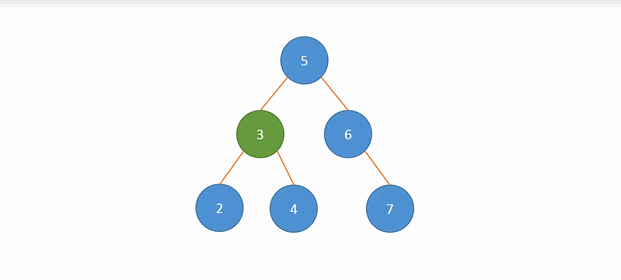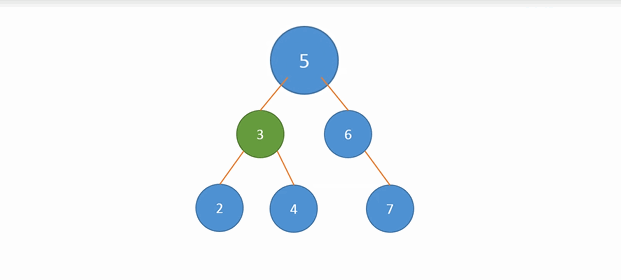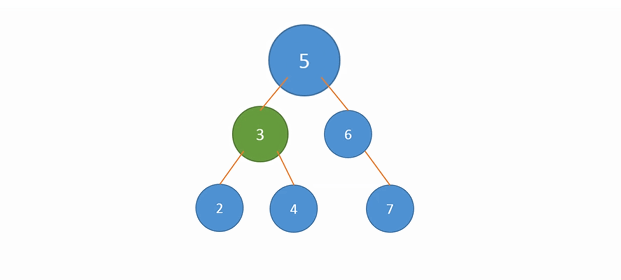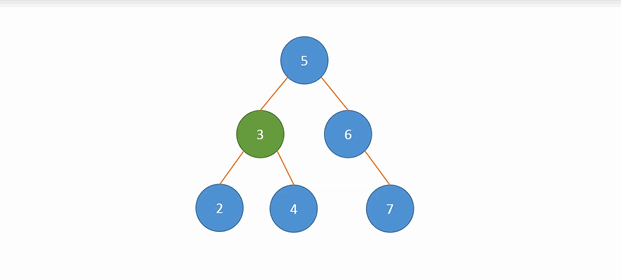
再写出第二种大情况,与上类似:
# 一定在右子树
elif nodei.val < key:
nodei.right = self.__delNodei(nodei.right,key)# 删除后返回nodei.right节点的引用
再写出第三种大情况,即找到了等于key节点,又分四种小情况:
被删除节点是叶子节点:直接返回None,就是摘除它了:
# nodei.val== key,删除nodei
else:
# 情况1:被删除节点是叶子节点
if not nodei.left and not nodei.right:
return None # 置为None
第二、三种小情况很相似,跳过被删除节点nodei,直接返回nodei.left 或 node.right 即可:
# 情况2:被删除节点无右子树
if not nodei.right:
return nodei.left # 跳过nodei,返回指向nodei.left,相当于删除了nodei
# 情况3:被删除节点无左子树
if not nodei.left:
return nodei.right
最后一种小情况,大家直接看注释吧:
# 情况4:被删除节点左右子树都不为空
# 先找到右子树中最左节点,即右子树最小值节点
minNodei = self.__findMinNode(nodei.right)
nodei.val = minNodei.val
# 删除minNodei,同时返回nodei.right的引用,并赋值给nodei.right
## 切记:key已经不是__delNodei的参数key,而是我们找到的minNodei的val值
nodei.right = self.__delNodei(nodei.right,minNodei.val)
return nodei
上面代码,删除节点3的动画演示: