【概率论】反直觉的三门问题，为什么80%的人都错了？-轻识

导读：在本文中我们将讨论条件概率：给定结果受到先前事件影响的概率。

作者：贝内迪克特·格罗斯、乔·哈里斯、埃米莉·里尔

来源：大数据DT（ID：hzdashuju）

01 三门问题

三门问题来源于一个被称作“让我们做个交易”的古老游戏节目中多次上演的一个场景。虽然这个场景的设置在细节上各不相同，但总体都差不多。

首先，主持人蒙提霍尔会选择一名观众来参与这个游戏。这名观众会看见三副门帘，其中一副门帘的后面会有一个值得期待的奖品（诺加海德革的一整套客厅套装或一辆汽车），在另外两副之后是有趣却没什么价值的奖品，比如山羊。游戏参与者要从三副门帘中选择其中一副，并且可以获得这副门帘后的奖品。

然而此时，蒙提霍尔会在揭晓选手所选门帘后面的奖品之前，打开其中一个未被选中的门帘，并揭晓门帘后面的山羊。然后，参与者可以坚持原来的选择或换成剩下的那副。问题是：参与者是否要改变呢？每种情况成功的概率是多少？

（注意到蒙提霍尔不是在参与者未选择的两扇门中随机地选择，并展示出那个门后的物品。他总是选取一个后面是羊的门。所以，如果参与者最初选了一扇有山羊的门，则蒙提霍尔无法选择打开哪扇门，他只能选择另一扇有山羊的门。但如果参与者最初选了有汽车的门，则蒙提霍尔可以从剩下的两个门中任选一个打开，此时他可以随机选择。）

首先要指出的是，如果你坚持原来的选择，那么获胜的可能性与蒙提霍尔选择之前一样：1/3。另外一方面，为了计算你的选择改变后选中的概率，我们可以列出选择改变后的结果：

你原来的猜测有1/3的可能性是正确的；在这种情况下你输了。但是：
你原来的猜测有2/3的可能性是错误的；在这种情况下你赢了。

这样，你的选择改变获胜的概率是2/3!

让我们来试试这个游戏的一些变形，看看会是什么结果。例如，如果有四扇门，后面有一辆汽车和三只山羊。我们玩同样的游戏：先选一扇门，蒙提霍尔给我们看是一只山羊，那么我们选择坚持还是改变？注意现在有四扇门。在这种情况下，每种选择的概率是多少？

像之前一样，如果我们坚持原来的选择，那么有1/4的概率会赢。如果我们决定选择剩余两扇门中的一扇门会是怎样？在这种情况下：

你原来的猜测有1/4的可能性是正确的；在这种情况下你输了，但是：
你原来的猜测有3/4的可能性是错误的。在这种情况下，赢的门是剩下的两扇中的一个，那么你有一半的机会猜对。

这样说吧：你将有3/4一半的可能性是正确的，也就是说3/8的可能性。同样，比坚持原来的选择要好。

此时，我们可以考虑n扇门时的情况，其中一扇门后同样是汽车，其他n-1扇门后是山羊。如果我们坚持原来的选择，和以前一样，获胜的概率是1/n。如果我们选择改变，逻辑是：

你原来的猜测有1/n的可能性是正确的；在这种情况下你输了。
你原来的猜测有1/n-1的可能性是错误的。在这种情况下，后面有车的门是剩下的n-2扇中的一个，那么你有1/(n-2)的机会猜对。

于是你获胜的概率就是

可以写成

因为n-1/n-2>1，所以我们发现改变总比坚持原来的选择的获胜概率1/n好。

我们不得不问：如果有多扇门和多辆汽车会是怎样？例如，假设有5扇门，后面有两辆车和3只山羊，该坚持还是改变？同样的逻辑仍然适用：如果你坚持原来的选择，获胜的概率只有2/5。另一方面，如果你选择改变：

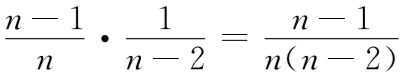
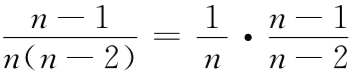
你原来的猜测有2/5的可能性是正确的。这时，在蒙提霍尔展示一只山羊之后，剩下的3扇门中有一辆汽车和两只山羊；在这种情况下，你赢的概率是1/3。
你原来的猜测有3/5的可能性是错误的。这时，剩下的3扇门后有两辆汽车和一只山羊；在这种情况下，你赢的概率是2/3。

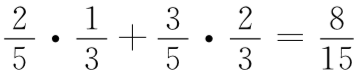
也就是说，2/5的时候你有1/3的机会获胜；3/5的时候你有2/3的机会获胜。因此，你获胜的概率是

此时，我们可以考虑有任意n扇门和任意k辆汽车的情形。（其实也不是完全任意的：至少要有3扇门，否则我们不能进行这个游戏；同样，至少要有两只山羊，使得无论你选择哪扇门蒙提霍尔都可以给你展示出一只山羊；换句话说，n≥3且k≤n-2。）在这种情况下，我们坚持原来选择的概率是k/n。另外一方面，如果我们选择改变，则由前面的逻辑得：

你原来的猜测有k/n的概率是正确的。在这种情形下，蒙提霍尔给你展示一只山羊后，剩下的n-2扇门中有k-1辆汽车和n-k-1只山羊；相应地，你获胜的概率为(k-1)/(n-2)。另外一方面：
你原来的猜测有(n-k)/n的概率是错误的。在这种情形下，剩下的 n-2扇门中有k辆汽车和n-k-2只山羊；你获胜的概率将是k/n-2。

将上面的概率加起来，你获胜的概率为

注意这总是大于k/n的（因为n-1比n-2大），所以最终结果是：总是要改变选择。

02 什么是条件概率

所有这些版本的三门问题都说明了条件概率的概念：我们不知道最初的猜测正确与否，但可以计算在这两种情形下的概率，并以此来确定获胜的概率。

为了具体起见，我们引入一些符号。一般情况下，用P(A)表示事件A发生的概率。例如，我们在分析有n扇门和k辆车的三门问题时，令A代表“我们初始猜测是正确的”这个事件，令B代表“我们初始猜测是错误的”这个事件，那么有

注意在一般情形下，P(A)是一个介于0和1之间的数，如果A是一个必然事件，则P(A)=1，如果A是一个不可能发生事件，那么P(A)=0。还要注意到，如果随机试验只有两个事件A和B，且A和B中有一个一定发生，但不会同时发生，则一定有

现在，我们考虑三门问题中通过改变选择后赢得游戏的事件，并用W表示。在这种情况下，我们也许开始并不知道W发生的概率，但知道如果A发生则W发生的概率。此时，记为P(W|A)。

同样，在蒙提霍尔的例子中，情况是这样的：假设开始的猜测是正确的，那么我们改变选择后赢的概率用新的符号可表示为

类似地

上式中，P(W∩A)表示A和W都发生的概率。事实上，我们可以看到

即A和W同时发生的概率（记为P(W∩A)）等于A发生的概率乘以已知A发生的条件下W发生的概率。

假设我们现在遇到的情形是要么A发生要么B发生，但不会同时发生。在计算上，这种情形对应于条件P(A)+P(B)=1。于是，说W发生就是说，要么W和A同时发生，要么W和B同时发生，即

此外，因为P(W∩A)=P(A)·P(W|A)，同样，对B也有类似的公式，因此可以将其写为更一般的公式：

设两个事件A或B会发生，但不同时发生。则对其结果可能依赖于A和B的第三个事件W，有

换句话说，假设事件A发生的概率为P(A)，那么在A发生的次数中，W发生的概率为P(W|A)；类似地，如果B发生的概率为P(B)，那么在这些次数中，W发生的概率为P(W|B)。于是W发生的总概率P(W)就是A和W同时发生的可能性P(A)·P(W|A)加上B和W同时发生的可能性P(B)·P(W|B)。

这正是在三门游戏中我们在计算决定改变策略而获胜的概率时所做的运算。

例如，如果P(A)=P(B)=1/2，即A和B的发生是等概率的，那么我们赢的概率就是P(W|A)和P(W|B)的平均，这是有意义的。当P(A)增加，则P(B)减小（这里因为A和B发生的概率之和为1），这样我们得到一个加权平均值，其中P(W|A)的权重更大一些；同样，这也是有意义的。

在这种设定下，我们称P(W|A)为假设A发生时获胜的条件概率；类似地，称P(W|B)为假设B发生时获胜的条件概率。

我们可以很自然地得到更一般的版本。如果n个事件A₁，…，A_n中有一个事件必须发生；设P(A_i)为A_i发生的概率。假设A_i发生的情形下获胜的概率是P(W|A_i)。于是获胜的概率P(W)是

问题1 有两个赌徒内森和卡尔，由于缺乏想象力，他们正在玩一个简单的游戏：每人掷一个骰子，点数高的人获胜。如果是平局，那么内森掷一个骰子来打破平局：如果是1、2、3或4，则内森获胜，如果是5或者6，则卡尔获胜。这给了内森多少优势？换言之，他获胜的概率是多大？

解第一次掷可能有三种结果：内森直接获胜，卡尔直接获胜，或者平局。将这些结果分别记为A_N，A_C，A_T，我们要做的第一件事就是确定它们发生的概率。

这很直接。内森和卡尔第一次掷骰子有36种可能的结果。其中6种是平局，剩下的30种结果中内森获胜和卡尔获胜的次数是相同的。于是，

下面的问题是，在给定第一次掷的结果后内森获胜的概率是多少呢？同样，这并不难计算：如果A_N发生了，则内森直接获胜；换句话说（或用符号表示），如果记内森获胜为W，那么

类似地，如果AC发生，那么内森将没有获胜的机会，也就是说，

最后，如果AT发生，即第一轮的结果是平局，那么内森将有4/6的概率会获胜，于是

现在我们只需把它们都加起来：根据前面的公式，得到

换句话说，内森将有19/36或约52。8%的概率赢得游戏。

下面用另外一个赌博游戏来说明条件概率这个概念：

问题2 内森和卡尔已经退步到玩掷硬币的游戏了。游戏规则如下：内森从一个装有三枚硬币的袋子里随机挑选一枚，然后进行投掷。如果是“正面”，则内森获胜，如果是“反面”，则卡尔获胜。有意思的是，袋子中有两枚硬币是“公平的”，即出现“正面”和“反面”的概率相同，但一枚是特制的：出现“反面”的概率是60%，即3/5，出现“正面”的概率只有2/5。问题是，内森获胜的概率有多大？

解因为我们不知道内森选择了哪枚硬币，所以不知道他投掷的概率是多少，但是知道每一种情况下的概率，所以可以使用我们的公式。按照这个逻辑：内森选择“公平”硬币的概率是2/3，在这种情况下，有一半的概率会获胜；他选择“特制”硬币的概率是1/3，在这种情况下，获胜的概率只有2/5。换句话说，内森获胜的概率是2/3的1/3加上1/3的2/5，即

用符号来表示的话：如果内森选择“公平”硬币的事件是A，选择“特制”硬币的事件是B，则有

现在，如果用W表示内森获胜，那么题设告诉我们

应用前面的公式，像之前一样，我们有

本文摘编自《哈佛概率论公开课》，经出版方授权发布。

延伸阅读《哈佛概率论公开课》点击上图了解及购买

推荐语：本书为对基本概率论感兴趣的读者以及之前未接触过此方向的人提供了一个坚实的基础。通过对话的方式和详细的数学推导，在迷人的风格和信息丰富的讨论上取得了平衡。


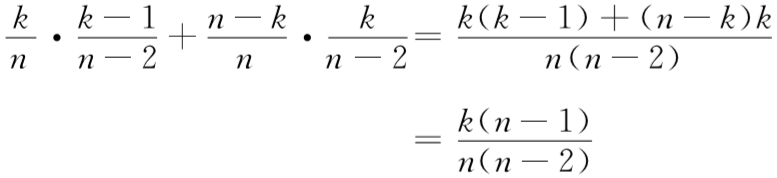
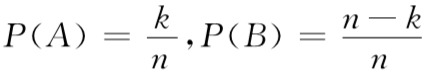
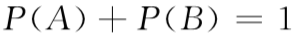
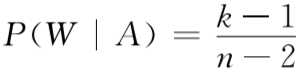
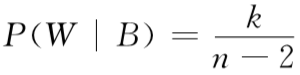
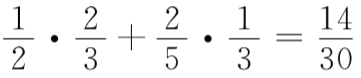
也可以加一下老胡的微信
围观朋友圈~~~

推荐阅读

（点击标题可跳转阅读）

深度学习的四个学习阶段！

2021年，机器学习研究风向要变了？

【机器学习】随机森林是我最喜欢的模型

Python之父：Python 4.0可能不会来了

【2021版】机器学习、深度学习调参手册

亚马逊首席科学家李沐博士：工作五年反思

【下载】80页笔记看遍机器学习基本概念、算法、模型

老铁，三连支持一下，好吗？↓↓↓