LeetCode 第224周周赛题解
【GiantPandaCV导语】这是LeetCode的第224场周赛的题解,本期考察的知识点有暴力,排序,记忆化搜索等等。
比赛链接
https://leetcode-cn.com/contest/weekly-contest-224/
题目一:可以形成最大正方形的矩形数目
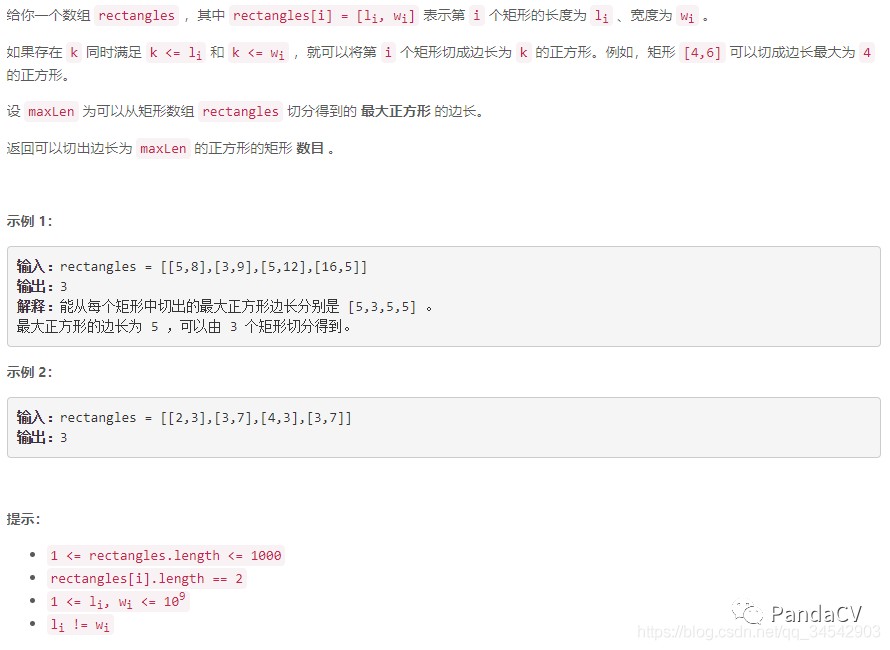
解题思路:直接暴力枚举每个正方形,然后保存下最大的边长,维护一下最大边长的个数即可。时间复杂度:解题代码如下:
class Solution {
public:
int countGoodRectangles(vector<vector<int>>& rectangles) {
int max_len=0,cnt=0;
for(int i=0;i {
int minlr=min(rectangles[i][0],rectangles[i][1]);
if(minlr==max_len)
cnt++;
else if(minlr>max_len)
{
cnt=1;
max_len=minlr;
}
}
return cnt;
}
};
题目二:同积元组

题面
解题思路:题目给出了不同正整数组成的数组,要求计算a*b=c*d的个数,首先想到的是对所有a*b的结果进行统计,由于数组中不存在相同的数,那么就可以直接对统计的结果进行计算即可,由于数的范围是1e4,这里采用map。时间复杂度:解题代码如下:
class Solution {
public:
int tupleSameProduct(vector<int>& nums) {
map<int,int> mp;
for(int i=0;i for(int j=i+1;j mp[nums[i]*nums[j]]++;
int ans=0;
for(auto it=mp.begin();it!=mp.end();it++)
{
int cnt =it->second;
ans += (cnt)*(cnt-1)/2*8;
}
return ans;
}
};
题目三:重新排列后的最大子矩阵

解题思路:题目给出一个01矩阵,可以将矩阵的列任意排列,求最大子矩阵的面积;我们可以先将每个点向下最长1的长度维护出来,然后对于每一行,将该行的每个最长的长度进行排序,遍历一遍这个排序后的向下高度,即可求出来以这行点为矩形左上起点的最大面积时间复杂度:解题代码如下:
class Solution {
public:
int largestSubmatrix(vector<vector<int>>& matrix) {
int n=matrix.size(),m=matrix[0].size();
vector<vector<int>> dp(n, vector<int>(m, 0));
for(int j=0;j {
for(int i=n-1;i>=0;i--)
{
if(matrix[i][j]==0)
dp[i][j]=0;
else
{
if(i==n-1)
dp[i][j]=1;
else
dp[i][j]= 1 +dp[i+1][j];
}
}
}
int ans=0;
for(int i=0;i {
vector<int> tmp;
for(int j=0;j tmp.push_back(dp[i][j]);
sort(tmp.rbegin(),tmp.rend());
for(int j=0;j ans=max(ans,tmp[j]*(j+1));
}
return ans;
}
};
题目四:猫和老鼠 II

解题思路:给出一个矩阵问猫和老鼠谁获胜,由于矩阵大小最大只有8*8,那么直接记忆化搜索即可,令dp[who][Mi][Mj][Ci][Cj][step]表示who在(鼠在Mi Mj,猫在Ci Cj)这个状态下走了step步时,是否存在必胜状态,如果为0表示还没有搜到,如果为1表示who在该状态下存在必胜策略,如果为-1表示必败。初始化为必败,然后不停的存在是否存在必胜策略。
1.如果who等于老鼠,必胜态为下一步能走到食物或者下一步走到的状态为必胜态。
2.如果who等于猫,那么猫的必胜状态为下一步走到食物或者下一步遇到老鼠或者下一步超过限制步数或者下一步为必胜态。
注意这样直接搜索可能会超时就有一些优化手段,首先是dp中的第一维who是两维,分别表示猫和老鼠,其实这一维可以去掉,用step%2表示即可,第二由于老鼠和猫都可以原地移动,那么对于某些图假设猫和老鼠都只能原地移动,其实这种图猫是必胜的,也就是说有些图可以剪枝,这里直接将步数限制在200步也可以通过。
时间复杂度:解题代码如下:
class Solution {
public:
mapvector<string>,int>,int> mmp;
int C,M,dir[4][2]= {-1,0,0,-1,1,0,0,1},n,m;
int dp[8][8][8][8][205];
void dfs(vector<string> &grid,int step,int Mi,int Mj,int Ci,int Cj)
{
int who= step%2;
if(step>=200) //步数超过200则直接判断
{
if(who==0) //如果当前是老鼠,则直接失败
dp[Mi][Mj][Ci][Cj][step]=-1;
else //如果当前是猫,则直接胜利
dp[Mi][Mj][Ci][Cj][step]=1;
return ;
}
dp[Mi][Mj][Ci][Cj][step]=-1; //初始化为失败,去寻找是否存在必胜策略
if(who==0) //who==0表示当前是老鼠
{
for(int i=0; i<4; i++)
{
for(int k=0; k<=M; k++)
{
int di= Mi +dir[i][0]*k;
int dj= Mj +dir[i][1]*k;
if(di>=0&&di=0&&dj {
if(grid[di][dj]=='#') //不能越过墙
break;
if(grid[di][dj]=='C')
continue;
else if(grid[di][dj]=='F') //如果是食物,则必胜,直接返回
{
dp[Mi][Mj][Ci][Cj][step]=1;
return ;
}
else //否则尝试走一步,判断下一步猫是否必败
{
swap(grid[Mi][Mj],grid[di][dj]);
if(dp[di][dj][Ci][Cj][step+1]==0)
dfs(grid,step+1,di,dj,Ci,Cj);
swap(grid[Mi][Mj],grid[di][dj]);
if(dp[di][dj][Ci][Cj][step+1]==-1) //如果下一步猫必败,则
{ //当前必胜
dp[Mi][Mj][Ci][Cj][step]=1;
return ;
}
}
}
}
}
}
else
{
for(int i=0; i<4; i++)
{
for(int k=0; k<=C; k++)
{
int di= Ci + dir[i][0]*k;
int dj= Cj + dir[i][1]*k;
if(di>=0&&di=0&&dj {
if(grid[di][dj]=='#')
break;
if(grid[di][dj]=='M'||grid[di][dj]=='F') //猫抓到老鼠或者食物
{
dp[Mi][Mj][Ci][Cj][step]=1;
return ;
}
else
{
swap(grid[Ci][Cj],grid[di][dj]);
if(dp[Mi][Mj][di][dj][step+1]==0) //同理
dfs(grid,step+1,Mi,Mj,di,dj);
swap(grid[Ci][Cj],grid[di][dj]);
if(dp[Mi][Mj][di][dj][step+1]==-1)
{
dp[Mi][Mj][Ci][Cj][step]=1;
return ;
}
}
}
}
}
}
}
bool canMouseWin(vector<string>& grid, int catJump, int mouseJump) {
C=catJump,M=mouseJump;
n=grid.size(),m=grid[0].size();
int CI,CJ,MI,MJ;
memset(dp,0,sizeof(dp));
for(int i=0; i for(int j=0; j {
if(grid[i][j]=='C')
CI=i,CJ=j;
if(grid[i][j]=='M')
MI=i,MJ=j;
}
dfs(grid,0,MI,MJ,CI,CJ);
if(dp[MI][MJ][CI][CJ][0]==1)
return true;
return false;
}
};
欢迎关注GiantPandaCV/PandaCV, 在这里你将看到独家的深度学习分享,坚持原创,每天分享我们学习到的新鲜知识。( • ̀ω•́ )✧
有对文章相关的问题,或者想要加入交流群,欢迎添加BBuf微信:
为了方便读者获取资料以及我们公众号的作者发布一些Github工程的更新,我们成立了一个QQ群,二维码如下,感兴趣可以加入。
