【机器学习】用 Hyperopt 和 Plotly 可视化超参数优化
来源:@公众号:数据STUDIO
在这篇文章中,云朵君将演示如何创建超参数设置的有效交互式可视化,使我们能够了解在超参数优化期间尝试的超参数设置之间的关系。本文的第 1 部分将使用 hyperopt 设置一个简单的超参数优化示例。在第 2 部分中,我们将展示如何使用Plotly创建由第 1 部分中的超参数优化生成的数据的交互式可视化。
hyperopt就是其中一个广泛使用的超参数优化框架包,它允许数据科学家通过定义目标函数和声明搜索空间来利用几种强大的算法进行超参数优化。然而,依靠这些工具可以将超参数选择变成一个“黑匣子”,这也导致了很难解释为什么一组特定的超参数最适合一个特定问题的特定模型。克服这些算法的“黑匣子”性质的一种方法,是可视化在超参数优化期间尝试过的超参数设置的历史,以帮助识别运行良好的超参数设置的潜在趋势。

写在前面
这篇文章假设读者熟悉超参数优化的概念。此外,尽管我们将创建一个示例超参数优化来生成可视化所需要的数据,但我们不会详细介绍此优化,因为本文的目的不是成为有关 hyperopt 的教程;这里有个不错的hyperopt 文档英文教程[1]。
为简洁起见,代码示例将假设所有必要的导入都已运行。作为参考,这里是代码示例所需的完整导入集:
from functools import partial
from pprint import pprint
import numpy as np
import pandas as pd
from hyperopt import fmin, hp, space_eval, tpe, STATUS_OK, Trials
from hyperopt.pyll import scope, stochastic
from plotly import express as px
from plotly import graph_objects as go
from plotly import offline as pyo
from sklearn.datasets import load_boston
from sklearn.ensemble import GradientBoostingRegressor, RandomForestRegressor
from sklearn.metrics import make_scorer, mean_squared_error
from sklearn.model_selection import cross_val_score, KFold
from sklearn.utils import check_random_state
pyo.init_notebook_mode()
使用 hyperopt 超参数优化示例
在我们使用 Plotly 进行可视化之前,我们需要从 hyperopt 生成一些超参数优化数据供我们可视化。我们需要遵循四个关键步骤来使用 hyperopt 设置超参数优化:
选择和加载数据集 声明超参数搜索空间 定义目标函数 运行超参数优化
我们将提供每个步骤的简要描述以及示例代码,但我们不会详细说明具体选择的合理性,因为这种超参数优化的目标只是为我们生成可视化数据。
选择和加载数据集
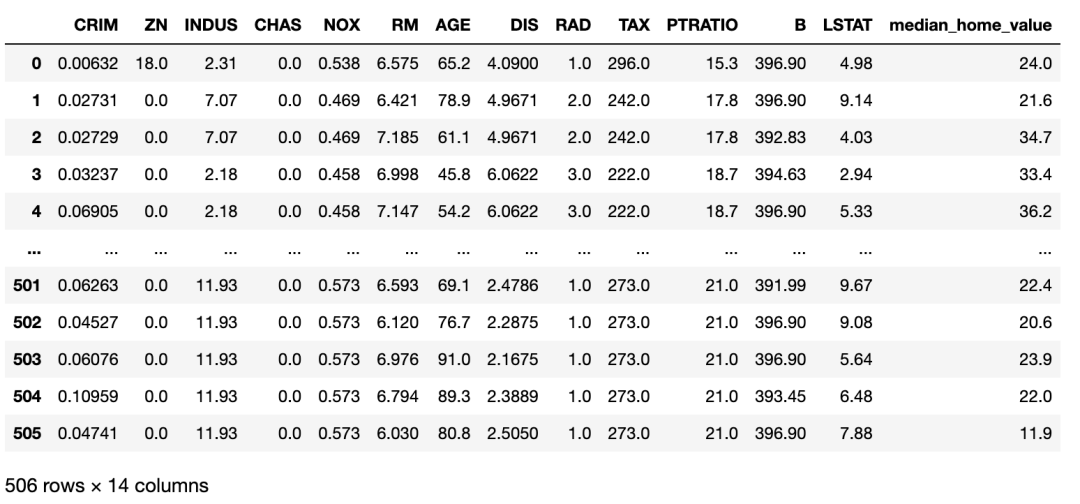
我们将使用UCI[2]波士顿数据集作为我们的超参数优化的示例数据集。UCI 波士顿数据集的特征是各种社区特征,目标是该社区房屋的中值。Scikit-learn 提供了一个方便的包装函数,名为load_boston。我们将使用此函数将数据集加载到 Pandas 数据框中,如下所示:
MEDIAN_HOME_VALUE = "median_home_value"
# 使用 sklearn 的辅助函数加载波士顿数据集
boston_dataset = load_boston()
# 将数据转换为 Pandas 数据框
data = np.concatenate(
[boston_dataset["data"], boston_dataset["target"][..., np.newaxis]],
axis=1,
)
features, target = boston_dataset["feature_names"], MEDIAN_HOME_VALUE
columns = np.concatenate([features, [target]])
boston_dataset_df = pd.DataFrame(data, columns=columns)
boston_dataset_df
定义超参数搜索空间
由于该数据集的目标是连续的,我们将要比较几个不同的回归模型。我们将设置超参数优化来比较两种类型的模型:随机森林回归器和梯度提升回归器(可以阅读文档戳➡️集成算法 | 随机森林回归模型)。随机森林回归器将允许 hyperopt 调整树的数量和每棵树的最大深度。除了树的数量和每棵树的最大深度之外,梯度提升回归器将允许 hyperopt 调整学习率。以下字典以 hyperopt 预期的格式声明此超参数搜索空间:
# 定义常量字符串,我们将在下面的“search space”字典中用作键。
# 注意,我在整个过程中使用的约定是,
# 用一个匹配该字符串的变量来表示字符串中的字符,只是变量中的字符是大写的。
# 这种约定允许我们在代码中遇到这些变量时很容易解释它们的含义。
# 例如,我们知道变量' MODEL '包含字符串" MODEL "。
# 用变量表示字符串的这种模式允许我在代码中重复使用同一个字符串时避免键入错误,
# 因为在变量名中键入错误将被检查器捕获为错误。
GRADIENT_BOOSTING_REGRESSOR = "gradient_boosting_regressor"
KWARGS = "kwargs"
LEARNING_RATE = "learning_rate"
LINEAR_REGRESSION = "linear_regression"
MAX_DEPTH = "max_depth"
MODEL = "model"
MODEL_CHOICE = "model_choice"
NORMALIZE = "normalize"
N_ESTIMATORS = "n_estimators"
RANDOM_FOREST_REGRESSOR = "random_forest_regressor"
RANDOM_STATE = "random_state"
# 声明随机森林回归模型的搜索空间。
random_forest_regressor = {
MODEL: RANDOM_FOREST_REGRESSOR,
# 我将模型参数定义为一个单独的字典,以便我们可以将参数输入
# 带有字典解包的模型的`__init__`。参见 `sample_to_model` 函数
# 与目标函数一起定义以查看此操作
KWARGS: {
N_ESTIMATORS: scope.int(
hp.quniform(f"{RANDOM_FOREST_REGRESSOR}__{N_ESTIMATORS}", 50, 150, 1)
),
MAX_DEPTH: scope.int(
hp.quniform(f"{RANDOM_FOREST_REGRESSOR}__{MAX_DEPTH}", 2, 12, 1)
),
RANDOM_STATE: 0,
},
}
# 声明梯度提升回归模型的搜索空间,
# 结构与随机森林回归搜索空间相同。
gradient_boosting_regressor = {
MODEL: GRADIENT_BOOSTING_REGRESSOR,
KWARGS: {
LEARNING_RATE: scope.float(
hp.uniform(f"{GRADIENT_BOOSTING_REGRESSOR}__{LEARNING_RATE}", 0.01, 0.15,)
), # lower learning rate
N_ESTIMATORS: scope.int(
hp.quniform(f"{GRADIENT_BOOSTING_REGRESSOR}__{N_ESTIMATORS}", 50, 150, 1)
),
MAX_DEPTH: scope.int(
hp.quniform(f"{GRADIENT_BOOSTING_REGRESSOR}__{MAX_DEPTH}", 2, 12, 1)
),
RANDOM_STATE: 0,
},
}
# 将两个模型搜索空间与两个模型之间的顶级“choice”结合起来,得到最终的搜索空间。
space = {
MODEL_CHOICE: hp.choice(
MODEL_CHOICE, [random_forest_regressor, gradient_boosting_regressor,],
)
}
定义目标函数
对于目标函数,我们将通过十折交叉验证计算数据集每个实例的均方误差。我们将打印折叠的平均均方误差作为损失。下面的代码定义了这个目标:
# 定义几个额外的变量来表示字符串。注意,这段代码期望我们能够
# 访问之前在"search space"代码片段中定义的所有变量。
LOSS = "loss"
STATUS = "status"
# 从字符串名称映射到模型类定义对象,我们将使用该对象
# 从hyperopt搜索空间生成的样本创建模型的初始化版本。
MODELS = {
GRADIENT_BOOSTING_REGRESSOR: GradientBoostingRegressor,
RANDOM_FOREST_REGRESSOR: RandomForestRegressor,
}
# 创建一个我们将在目标中使用的评分函数
mse_scorer = make_scorer(mean_squared_error)
# 从hyperopt生成的示例转换为初始化模型的辅助函数。
# 注意,因为我们在搜索空间声明中将模型类型和模型关键字-参数分割成单独的键-值对,# 所以我们能够使用字典解包来创建模型的初始化版本。
def sample_to_model(sample):
kwargs = sample[MODEL_CHOICE][KWARGS]
return MODELS[sample[MODEL_CHOICE][MODEL]](**kwargs "sample[MODEL_CHOICE][MODEL]")
# 定义hyperopt的目标函数。我们将使用 `functools.partial` 修复`dataset`, `features`, 和 `target` 参数。
# 来创建这个函数的那个版本, 并将其作为参数提供给 `fmin`
def objective(sample, dataset_df, features, target):
model = sample_to_model(sample)
rng = check_random_state(0)
# 处理随机洗牌时创建折叠。在现实中,
# 我们可能需要比上述生成的固定“RandomState”实例更好的策略来管理随机性。
cv = KFold(n_splits=10, random_state=rng, shuffle=True)
# 计算每一次的平均均方误差。由于`n_splits` 是10,`mse` 将是一个大小为10的数组,
# 每个元素表示一次折叠的平均平均平方误差。
mse = cross_val_score(
model,
dataset_df.loc[:, features],
dataset_df.loc[:, target],
scoring=mse_scorer,
cv=cv,
)
# 返回所有折叠的均方误差的平均值。
return {LOSS: np.mean(mse), STATUS: STATUS_OK}
运行超参数优化
我们将通过调用fmin函数运行一千次试验的超参数优化。重要的是,我们将提供一个Trials对象的实例,hyperopt 将在其中记录超参数优化的每次迭代的超参数设置。我们将从这个Trials实例中提取可视化数据。运行以下代码执行超参数优化:
# 我们自定义的目标函数是通用的数据集,
# 我们需要使用`partial` 从`functools` 模块来"fix"这个`dataset_df`, `features`, 和 `target` 的参数值,
# 希望在这个例子中,我们有一个目标函数只接受一个参数假设的“hyperopt”界面。
boston_objective = partial(
objective, dataset_df=boston_dataset_df, features=features, target=MEDIAN_HOME_VALUE
)
# `hyperopt` 跟踪这个`Trials`对象的每次迭代的结果。
# 我们将从这个对象中收集用于可视化的数据。
trials = Trials()
rng = check_random_state(0) # reproducibility!
# `fmin`搜索“minimize”我们的对象的超参数,均方误差,并返回超参数的“best”集。
best = fmin(boston_objective, space, tpe.suggest, 1000, trials=trials, rstate=rng)
超参数优化可视化
Hyperopt 记录在超参数优化期间尝试的超参数设置的历史记录在我们作为参数提供给调用 fmin 的 Trials 对象的实例中。优化完成后,我们可以检查trials变量以查看 hyperopt 为前五个试验选择了哪些设置,如下所示:
pprint([t for t in trials][:5])[{'book_time': datetime.datetime(2020, 11, 4, 0, 51, 42, 199000),
'exp_key': None,
'misc': {'cmd': ('domain_attachment', 'FMinIter_Domain'),
'idxs': {'gradient_boosting_regressor__learning_rate': [],
'gradient_boosting_regressor__max_depth': [],
'gradient_boosting_regressor__n_estimators': [],
'model_choice': [0],
'random_forest_regressor__max_depth': [0],
'random_forest_regressor__n_estimators': [0]},
'tid': 0,
'vals': {'gradient_boosting_regressor__learning_rate': [],
'gradient_boosting_regressor__max_depth': [],
'gradient_boosting_regressor__n_estimators': [],
'model_choice': [0],
'random_forest_regressor__max_depth': [5.0],
'random_forest_regressor__n_estimators': [90.0]},
'workdir': None},
'owner': None,
'refresh_time': datetime.datetime(2020, 11, 4, 0, 51, 46, 83000),
'result': {'loss': 16.359897953574603, 'status': 'ok'},
'spec': None,
'state': 2,
'tid': 0,
'version': 0},
{'book_time': datetime.datetime(2020, 11, 4, 0, 51, 46, 92000),
'exp_key': None,
'misc': {'cmd': ('domain_attachment', 'FMinIter_Domain'),
'idxs': {'gradient_boosting_regressor__learning_rate': [1],
'gradient_boosting_regressor__max_depth': [1],
'gradient_boosting_regressor__n_estimators': [1],
'model_choice': [1],
'random_forest_regressor__max_depth': [],
'random_forest_regressor__n_estimators': []},
'tid': 1,
'vals': {'gradient_boosting_regressor__learning_rate': [0.03819110609989756],
'gradient_boosting_regressor__max_depth': [8.0],
'gradient_boosting_regressor__n_estimators': [137.0],
'model_choice': [1],
'random_forest_regressor__max_depth': [],
'random_forest_regressor__n_estimators': []},
'workdir': None},
'owner': None,
'refresh_time': datetime.datetime(2020, 11, 4, 0, 51, 52, 70000),
'result': {'loss': 18.045981512632412, 'status': 'ok'},
'spec': None,
'state': 2,
'tid': 1,
'version': 0},
{'book_time': datetime.datetime(2020, 11, 4, 0, 51, 52, 81000),
'exp_key': None,
'misc': {'cmd': ('domain_attachment', 'FMinIter_Domain'),
'idxs': {'gradient_boosting_regressor__learning_rate': [2],
'gradient_boosting_regressor__max_depth': [2],
'gradient_boosting_regressor__n_estimators': [2],
'model_choice': [2],
'random_forest_regressor__max_depth': [],
'random_forest_regressor__n_estimators': []},
'tid': 2,
'vals': {'gradient_boosting_regressor__learning_rate': [0.08587985607913044],
'gradient_boosting_regressor__max_depth': [12.0],
'gradient_boosting_regressor__n_estimators': [95.0],
'model_choice': [1],
'random_forest_regressor__max_depth': [],
'random_forest_regressor__n_estimators': []},
'workdir': None},
'owner': None,
'refresh_time': datetime.datetime(2020, 11, 4, 0, 51, 57, 519000),
'result': {'loss': 21.235091223167437, 'status': 'ok'},
'spec': None,
'state': 2,
'tid': 2,
'version': 0},
{'book_time': datetime.datetime(2020, 11, 4, 0, 51, 57, 528000),
'exp_key': None,
'misc': {'cmd': ('domain_attachment', 'FMinIter_Domain'),
'idxs': {'gradient_boosting_regressor__learning_rate': [],
'gradient_boosting_regressor__max_depth': [],
'gradient_boosting_regressor__n_estimators': [],
'model_choice': [3],
'random_forest_regressor__max_depth': [3],
'random_forest_regressor__n_estimators': [3]},
'tid': 3,
'vals': {'gradient_boosting_regressor__learning_rate': [],
'gradient_boosting_regressor__max_depth': [],
'gradient_boosting_regressor__n_estimators': [],
'model_choice': [0],
'random_forest_regressor__max_depth': [2.0],
'random_forest_regressor__n_estimators': [93.0]},
'workdir': None},
'owner': None,
'refresh_time': datetime.datetime(2020, 11, 4, 0, 52, 0, 661000),
'result': {'loss': 23.582397665666413, 'status': 'ok'},
'spec': None,
'state': 2,
'tid': 3,
'version': 0},
{'book_time': datetime.datetime(2020, 11, 4, 0, 52, 0, 670000),
'exp_key': None,
'misc': {'cmd': ('domain_attachment', 'FMinIter_Domain'),
'idxs': {'gradient_boosting_regressor__learning_rate': [4],
'gradient_boosting_regressor__max_depth': [4],
'gradient_boosting_regressor__n_estimators': [4],
'model_choice': [4],
'random_forest_regressor__max_depth': [],
'random_forest_regressor__n_estimators': []},
'tid': 4,
'vals': {'gradient_boosting_regressor__learning_rate': [0.0638511443414372],
'gradient_boosting_regressor__max_depth': [5.0],
'gradient_boosting_regressor__n_estimators': [72.0],
'model_choice': [1],
'random_forest_regressor__max_depth': [],
'random_forest_regressor__n_estimators': []},
'workdir': None},
'owner': None,
'refresh_time': datetime.datetime(2020, 11, 4, 0, 52, 2, 875000),
'result': {'loss': 15.253327611719737, 'status': 'ok'},
'spec': None,
'state': 2,
'tid': 4,
'version': 0}]上下滑动查看更多
如你所见,“trials”对象本质上是一个字典列表,其中每个字典都包含有关超参数优化的一次迭代的详细数据。这不是一种特别容易操作的格式,因此我们将数据的相关位转换为“Pandas”数据帧,其中数据帧的每一行都包含一次试验的信息:
# 这是一个简单的辅助函数,当一个特定的超参数与一个特定的试验无关时,
# 允许我们填充`np.nan`。
def unpack(x):
if x:
return x[0]
return np.nan
# 我们将首先将每个试验转换为一个系列,然后将这些系列堆叠在一起作为一个数据框架。
trials_df = pd.DataFrame([pd.Series(t["misc"]["vals"]).apply(unpack) for t in trials])
# 然后,我们将添加其他相关的信息到正确的行,并执行一些方便的映射
trials_df["loss"] = [t["result"]["loss"] for t in trials]
trials_df["trial_number"] = trials_df.index
trials_df[MODEL_CHOICE] = trials_df[MODEL_CHOICE].apply(
lambda x: RANDOM_FOREST_REGRESSOR if x == 0 else GRADIENT_BOOSTING_REGRESSOR
我们再看一下这种新格式的前五个试验:

这比我们之前的字典列表更易于管理。
使用 Plotly Express 绘制试验数量与损失
可视化试验迭代的一种有用方法是绘制试验次数与损失的关系图,以查看超参数优化是否如我们预期的那样随时间收敛。使用 Plotly 的高级Express[3]界面使这变得容易;我们只需在我们的数据帧上调用scatter方法并指出我们想要使用哪些列作为 x 和 y 值:
# px是“express”的别名,它是按照导入“express”的约定通过运行
# “from plotly import express as px”创建的。
fig = px.scatter(trials_df, x="trial_number", y="loss")
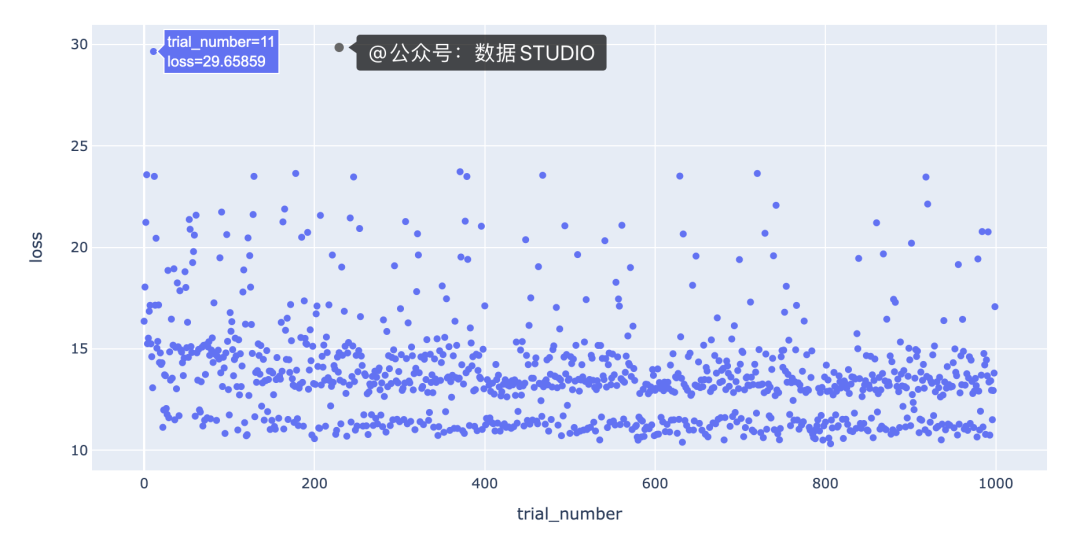
该图的一个有趣特征是,底行具有“损失”值在 10 到 12 之间的点与其余点之间存在明显的分隔。我们需要更多信息来了解导致这种分离的原因。一种假设是分离是由不同的模型类型引起的;例如,底行的点可能都是梯度提升回归模型,其余的点可能都是随机森林回归模型。
我们对每种模型类型的点进行不同的着色,以查看是否是这种情况,方法是color在方法调用中添加一个参数,scatter如下所示:
fig = px.scatter(trials_df,
x="trial_number",
y="loss",
color=MODEL_CHOICE)
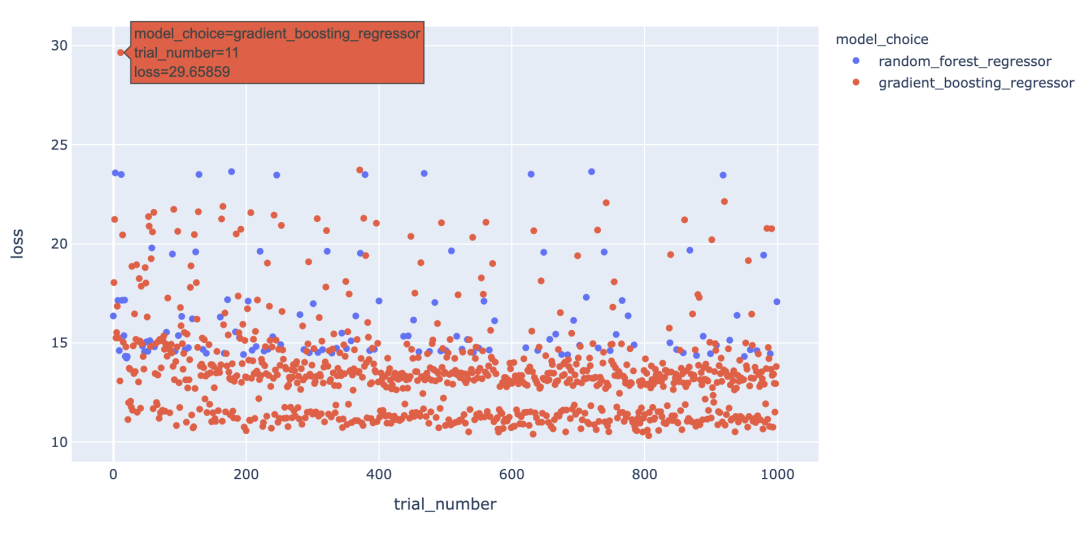
有趣的是,我们看到模型类型并不能完全解释底行点与其余点之间的差距,因为梯度提升回归模型也出现在其余点中。
我们可以通过创建交互式可视化来为可视化中的信息添加更多深度,这样当我们将鼠标悬停在每个点上时,我们可以看到导致该点丢失的一组超参数。起初,看起来我们应该能够通过简单地为hover_datascatter 方法的参数包含一个值来实现这一点。但是,由于我们只想为每个点包含与每种模型类型相关的超参数,因此我们需要在update_trace调用 scatter 之后调用该方法以添加悬停数据,因为这允许我们过滤为每个点显示哪些超参数观点。看起来是这样的
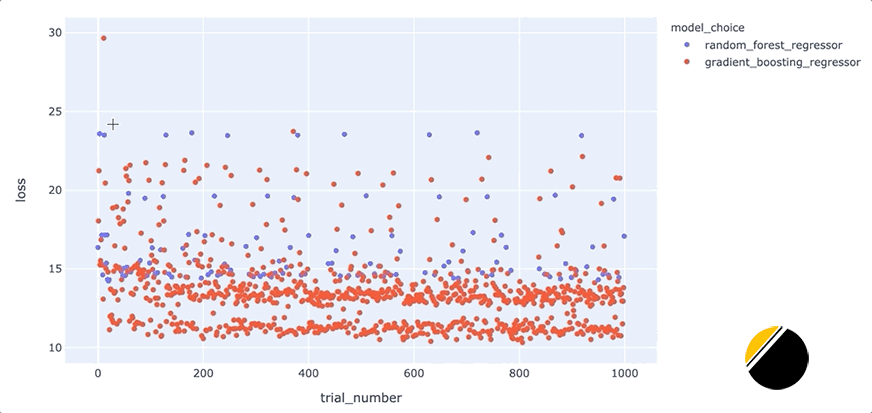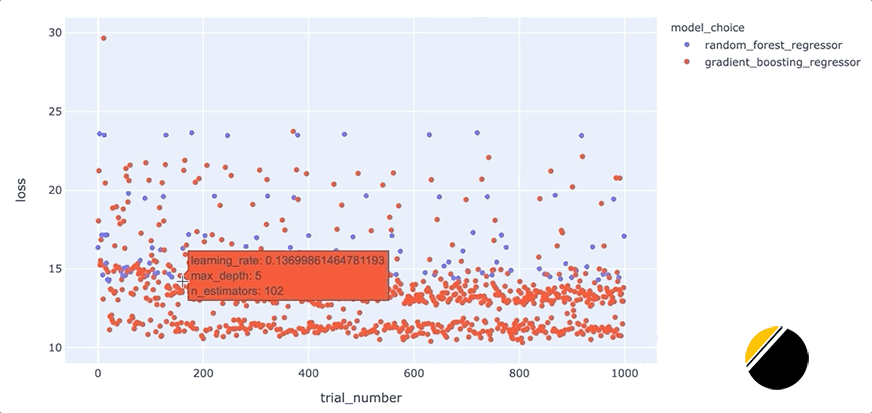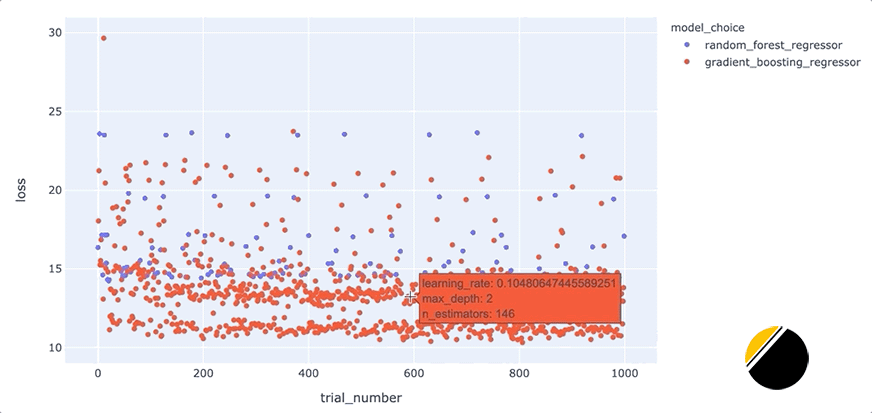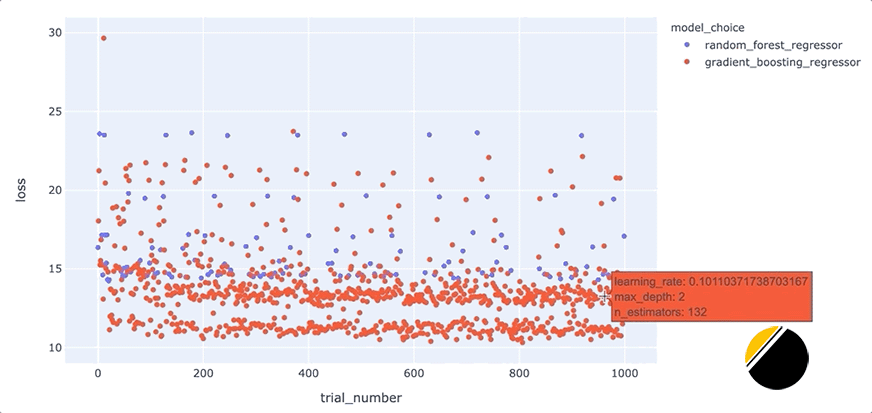
我们可以通过这些额外的细节来说明什么?将鼠标悬停在与底行中最佳模型相对应的点上,可以发现max_depth每个点的参数设置为3。
此外,将鼠标悬停在该行之外的点上会显示参数max_depth设置为3以外的值,例如2、4或5。这表明在我们的数据集中,参数max_depth可能有一些特殊之处。例如,这可能表明模型性能主要由三个特征驱动。我们将希望进一步研究为什么max_depth=3对我们的数据集如此有效,并且我们可能希望为我们构建和部署的最终模型将max_depth设置为3。
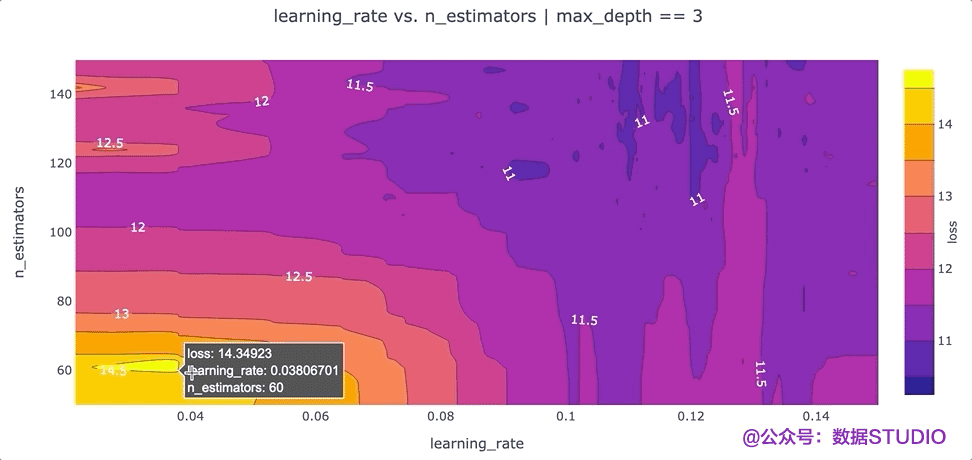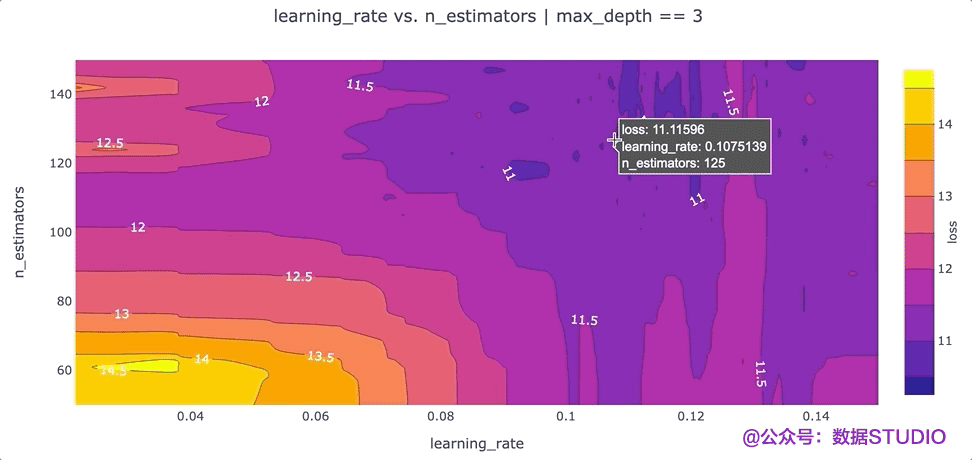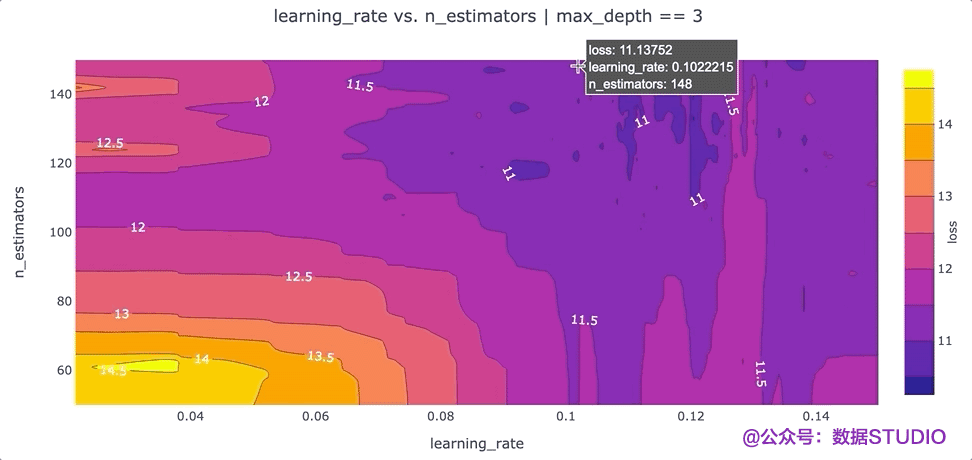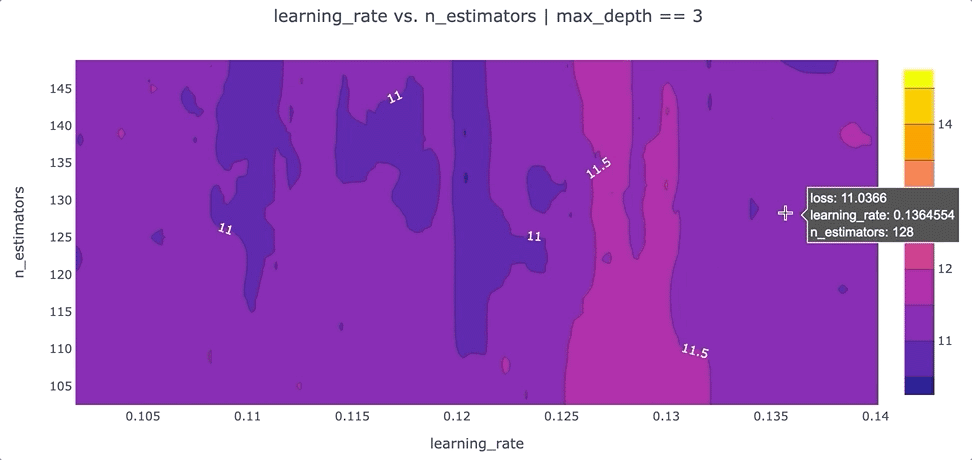
在特征之间创建等高线图
另一个可以提高我们对超参数设置直觉的可视化是根据超参数的“损失”值的等高线图。等高线图特别强大,因为它们揭示了不同超参数设置之间的交互如何影响损失。通常,我们希望为每对超参数生成一个单独的等高线图。在这种情况下,为了简单起见,我们max_depth将超参数的值固定为 3,并绘制该数据切片的learning_ratevs.n_estimatorsloss 等值线。我们可以通过运行以下命令使用 Plotly 创建这个等高线图:
# plotly express不支持轮廓图,
# 所以我们将使用'graph_objects'来代替。
# `go.Contour`自动为我们的损失插入“z”值。
fig = go.Figure(
data=go.Contour(
z=trials_df.loc[max_depth_filter, "loss"],
x=trials_df.loc[max_depth_filter, "gradient_boosting_regressor__learning_rate"],
y=trials_df.loc[max_depth_filter, "gradient_boosting_regressor__n_estimators"],
contours=dict(
showlabels=True, # 显示轮廓上的标签
labelfont=dict(size=12, color="white",),
# 标签字体属性
),
colorbar=dict(title="loss", titleside="right",),
hovertemplate="loss: %{z}
learning_rate: %{x}
n_estimators: %{y}
)
)
fig.update_layout(
xaxis_title="learning_rate",
yaxis_title="n_estimators",
title={
"text": "learning_rate vs. n_estimators | max_depth == 3",
"xanchor": "center",
"yanchor": "top",
"x": 0.5,
},
)
该图的一个要点是,我们可能希望尝试增加最大值n_estimators超参数,因为损失最低的区域出现在该图的顶部。
写在最后
在这篇文章中,我们介绍了如何将试验对象中包含的数据转换为 Pandas 数据框,以便我们可以轻松分析超参数设置的历史。一旦我们在数据框中获得了数据,我们就可以轻松地创建可视化,让我们更好地了解为什么一组特定的超参数设置是最好的。特别是,我们已经证明,通过使用 Plotly 创建简单的交互式可视化来增加可视化的深度,可以揭示一些非常适合我们的问题的超参数设置的有趣趋势。此外,我们已经展示了等高线图对于指示我们可能想要对超参数搜索空间进行的调整很有用。
原文链接: https://medium.com/doma/visualizing-hyperparameter-optimization-with-hyperopt-and-plotly-states-title 来源:@公众号:数据STUDIO
参考资料
hyperopt 文档英文教程:https://github.com/hyperopt/hyperopt/wiki/FMin#22-a-search-space-example-scikit-learn
[2]UCI:https://gitee.com/yunduodatastudio/picture/blob/master/data/ICU.png
[3]Express:https://plotly.com/python/plotly-express/
推荐阅读
